江苏苏州高新区2020年数学中考一模试卷
试卷更新日期:2020-06-23 类型:中考模拟
一、选择题
-
1. 9的算术平方根是( )A、 3 B、 C、 D、812. 2022 年冬奥会由北京和张家口两市联合承办.北京到张家口的自驾距离约为196000 米.196000 用科学记数法表示应为( )A、 1.96×105 B、19.6×104 C、1.96×106 D、0.196×1063. 下列四个图形中,既是轴对称图形又是中心对称图形的有( )
 A、4个 B、3个 C、2个 D、1个4. 若分式 在实数范围内有意义,则实数 的取值范围是A、 B、 C、 D、5. 一组数据1,3,6,1,2的众数与中位数分别是( )A、1,6 B、1,1 C、2,1 D、1,26. 若二次函数y=x2+bx的图象的对称轴是经过点(2,0)且平行于y轴的直线,则关于x的方程x2+bx =5的解为( )A、 B、 C、 D、7. 如图,某海监船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处时,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,此时海监船与岛屿P之间的距离(即PC的长)为( )
A、4个 B、3个 C、2个 D、1个4. 若分式 在实数范围内有意义,则实数 的取值范围是A、 B、 C、 D、5. 一组数据1,3,6,1,2的众数与中位数分别是( )A、1,6 B、1,1 C、2,1 D、1,26. 若二次函数y=x2+bx的图象的对称轴是经过点(2,0)且平行于y轴的直线,则关于x的方程x2+bx =5的解为( )A、 B、 C、 D、7. 如图,某海监船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处时,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,此时海监船与岛屿P之间的距离(即PC的长)为( )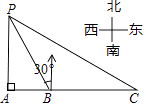 A、40海里 B、60海里 C、20 海里 D、40 海里8. 如图,有一块边长为2 的正方形厚纸板ABCD,做成如图①所示的一套七巧板(点O为正方形纸板对角线的交点,点E,F分别为AD,CD的中点,CE∥BI,IH∥CD),将图①所示七巧板拼成如图②所示的“鱼形”,则“鱼尾”MN的长为( )
A、40海里 B、60海里 C、20 海里 D、40 海里8. 如图,有一块边长为2 的正方形厚纸板ABCD,做成如图①所示的一套七巧板(点O为正方形纸板对角线的交点,点E,F分别为AD,CD的中点,CE∥BI,IH∥CD),将图①所示七巧板拼成如图②所示的“鱼形”,则“鱼尾”MN的长为( )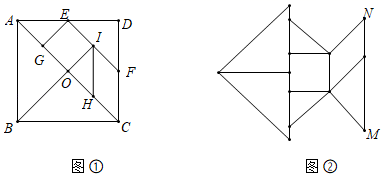 A、2 B、2 C、3 D、39. 如图,点 的坐标是(-1,0),点 的坐标是(0,6), 为 的中点,将 绕点 逆时针旋转90°.后得到 .若反比例函数 的图像恰好经过 的中点 ,则k的值是( )
A、2 B、2 C、3 D、39. 如图,点 的坐标是(-1,0),点 的坐标是(0,6), 为 的中点,将 绕点 逆时针旋转90°.后得到 .若反比例函数 的图像恰好经过 的中点 ,则k的值是( )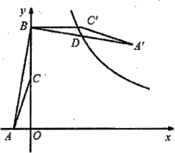 A、19 B、16.5 C、14 D、11.510. 如图,扇形OAB中,∠AOB=90°,将扇形OAB绕点B逆时针旋转,得到扇形BDC,若点O刚好落在弧AB上的点D处,则 的值为( )
A、19 B、16.5 C、14 D、11.510. 如图,扇形OAB中,∠AOB=90°,将扇形OAB绕点B逆时针旋转,得到扇形BDC,若点O刚好落在弧AB上的点D处,则 的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算a3÷a2的结果等于.12. 分解因式:2a2+4a+2= .13. 五边形的内角和是°.14. 某十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当你抬头看信号灯时,是绿灯的概率为 .
15. 如图,圆锥的底面半径为3cm,母线长为6cm,那么这个圆锥的侧面积是cm2(结果保留π).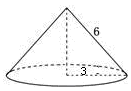 16. 如图,直线 与 轴交于点 ,以 为斜边在 轴上方作等腰直角 ,将 沿 轴向右平移,当点 中点落在直线 上时,则 平移的距离是.
16. 如图,直线 与 轴交于点 ,以 为斜边在 轴上方作等腰直角 ,将 沿 轴向右平移,当点 中点落在直线 上时,则 平移的距离是. 17. 如图,矩形ABCD中,E为BC的中点,将△ABE沿直线AE折叠时点B落在点F处,连接FC,若∠DAF=18°,则∠DCF=度.
17. 如图,矩形ABCD中,E为BC的中点,将△ABE沿直线AE折叠时点B落在点F处,连接FC,若∠DAF=18°,则∠DCF=度.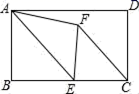 18. 如图,抛物线 与 轴交于 两点, 是以点 为圆心,2为半径的圆上的动点, 是线段 的中点,连结 .则线段 的最大值是.
18. 如图,抛物线 与 轴交于 两点, 是以点 为圆心,2为半径的圆上的动点, 是线段 的中点,连结 .则线段 的最大值是.
三、解答题
-
19. 计算: ﹣|﹣2|+( )﹣1﹣2cos45°20. 解不等式组: .21. 先化简,再求值.22. 甲、乙、丙、丁四名同学进行一次乒乓球单打比赛,要从中选两位同学打第一场比赛.(1)、若由甲挑一名选手打第一场比赛,选中乙的概率是;(2)、任选两名同学打第一场,求恰好选中甲、乙两位同学的概率.23. 为了解某校学生的课余兴趣爱好情况,某调查小组设计了“阅读”、“打球”、“书法”和“其他”四个选项,用随机抽样的方法调查了该校部分学生的课余兴趣爱好情况(每个学生必须选一项且只能选一项),并根据调查结果绘制了如下统计图:
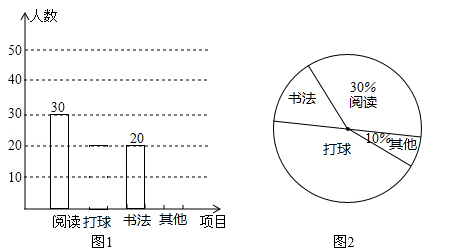
根据统计图所提供的信息,解答下列问题:
(1)、本次抽样调查中的样本容量是;(2)、补全条形统计图;(3)、该校共有2000名学生,请根据统计结果估计该校课余兴趣爱好为“打球”的学生人数.24.如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
 (1)、证明:四边形ACDE是平行四边形;(2)、若AC=8,BD=6,求△ADE的周长.25. 如图,反比例函数 的图象与一次函数 的图象交于两点 , .(1)、求反比例函数与一次函数的函数表达式;(2)、在反比例函数的图象上找点 ,使得点 构成以 为底的等腰三角形,请求出所有满足条件的点 的坐标.
(1)、证明:四边形ACDE是平行四边形;(2)、若AC=8,BD=6,求△ADE的周长.25. 如图,反比例函数 的图象与一次函数 的图象交于两点 , .(1)、求反比例函数与一次函数的函数表达式;(2)、在反比例函数的图象上找点 ,使得点 构成以 为底的等腰三角形,请求出所有满足条件的点 的坐标. 26. 如图,AB是⊙O的直径,AB=4 ,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.
26. 如图,AB是⊙O的直径,AB=4 ,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.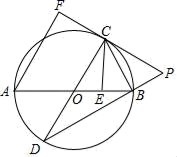 (1)、求证:CB是∠ECP的平分线;(2)、求证:CF=CE;(3)、当 时,求劣弧 的长度(结果保留π)27. 如图1,在 中, ,点 从点 出发以 的速度沿折线 运动,点 从点 出发以 的速度沿 运动, , 两点同时出发,当某一点运动到点 时,两点同时停止运动.设运动时间为 , 的面积为 , 关于 的函数图象由 , 两段组成,如图2所示.
(1)、求证:CB是∠ECP的平分线;(2)、求证:CF=CE;(3)、当 时,求劣弧 的长度(结果保留π)27. 如图1,在 中, ,点 从点 出发以 的速度沿折线 运动,点 从点 出发以 的速度沿 运动, , 两点同时出发,当某一点运动到点 时,两点同时停止运动.设运动时间为 , 的面积为 , 关于 的函数图象由 , 两段组成,如图2所示. (1)、求 的值;(2)、求图2中图象 段的函数表达式;(3)、当点 运动到线段 上某一段时 的面积,大于当点 在线段 上任意一点时 的面积,求 的取值范围.28. 在平面直角坐标系中,抛物线 与 轴交于 两点(点 在点 左侧),与 轴交于点 ,连接 ,将 沿 所在的直线翻折,得到 ,连接 .
(1)、求 的值;(2)、求图2中图象 段的函数表达式;(3)、当点 运动到线段 上某一段时 的面积,大于当点 在线段 上任意一点时 的面积,求 的取值范围.28. 在平面直角坐标系中,抛物线 与 轴交于 两点(点 在点 左侧),与 轴交于点 ,连接 ,将 沿 所在的直线翻折,得到 ,连接 .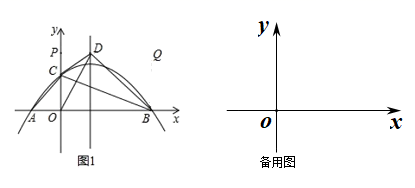 (1)、点 的坐标为 , 点 的坐标为;(2)、如图1,若点 落在抛物线的对称轴上,且在 轴上方,求抛物线的解析式.(3)、设 的面积为 , 的面积为 ,若 ,求 的值.
(1)、点 的坐标为 , 点 的坐标为;(2)、如图1,若点 落在抛物线的对称轴上,且在 轴上方,求抛物线的解析式.(3)、设 的面积为 , 的面积为 ,若 ,求 的值.