山东德州市武城县2018-2019学年八年级下学期数学期末试卷

试卷更新日期：2020-06-23 类型：期末考试

进入出卷网下载

一、单选题

1. 式子 $\frac{1}{\sqrt{x - 1}}$ 在实数范围内有意义，则x的取值范围是（）

A、x＜1 B、x≤1 C、x＞1 D、x≥1

查看试题解析
2. 根据下表中一次函数的自变量x与函数y的对应值，可得p的值为（）

x

－2

0

1

y

3

p

0

A、1 B、－1 C、3 D、－3

查看试题解析
3. 如图，在平行四边形ABCD中，∠ABC的平分线交AD于E，∠BED=150°，则∠A的大小为（）

A、150° B、130° C、120° D、100°

查看试题解析
4. 若 $\sqrt{x + y - 1} + {(y + 3)}^{2} = 0$ ，则 $x - y$ 的值为（）

A、1 B、-1 C、-7 D、7

查看试题解析
5. 函数 $y = (m + 1) x - (4 m - 3)$ 的图像经过一、二、四象限，则 $m$ 的取值范围是（）

A、 $m < \frac{3}{4}$ B、 $- 1 < m < \frac{3}{4}$ C、 $m < - 1$ D、 $m > - 1$

查看试题解析
6. 某车间5月上旬生产零件的次品数如下（单位：个）：0，2，0，2，3，0，2，3，1，1．则在这10天中该车间生产零件的次品数的（）

A、众数是3 B、中位数是1.5 C、平均数是2 D、以上都不符合题意

查看试题解析
7. 若直线y=ax+b的图象经过点（1，5），则关于 $x$ 的方程 $a x + b = 5$ 的解为（）

A、 $x = - 5$ B、 $x = 5$ C、 $x = 1$ D、 $x = - 1$

查看试题解析
8. 已知点（-2，y₁），（-1，y₂），（1，y₃）都在直线y=－3x＋b上，则y₁ ， y₂ ， y₃的值的大小关系是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{1} > y_{2} > y_{3}$ C、 $y_{3} > y_{1} > y_{2}$ D、 $y_{3} < y_{1} < y_{2}$

查看试题解析
9. 在直角坐标系中，函数y=kx与 $y = \frac{1}{2} x - k$ 的图像大数是（）

A、 B、 C、 D、

查看试题解析
10. 对于函数y=﹣5x+1，下列结论：
①它的图象必经过点（﹣1，5）

②它的图象经过第一、二、三象限

③当x＞1时，y＜0

④y的值随x值的增大而增大，

其中正确的个数是（　　）

A、0 B、1 C、2 D、3

查看试题解析
11.
如图，正方形ABCD中，AB=6，点E在边CD上，且CD=3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG、CF．下列结论：①△ABG≌△AFG；②BG=GC；③AG∥CF；④S_△_FGC=3．其中正确结论的个数是（　　）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

12. 把（a-2） $\sqrt{\frac{1}{2 - a}}$ 根号外的因式移到根号内,其结果为.

查看试题解析
13. 下面是甲、乙两人10次射击成绩（环数）的条形统计图，则这两人10次射击命中环数的方差 $s_{甲}^{2}$ $s_{乙}^{2}$ ．（填“＞”、“＜”或“＝”）

查看试题解析
14. 若点M（k﹣1，k+1）关于y轴的对称点在第四象限内，则一次函数y=（k﹣1）x+k的图象不经过第象限．

查看试题解析
15. 把两个同样大小的含45°角的三角尺按如图所示的方式放置，其中一个三角尺的锐角顶点与另一个的直角顶点重合于点A，且另三个锐角顶点B，C，D在同一直线上．若AB= $\sqrt{2}$ ，则CD= ．

查看试题解析
16.
如图所示，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为．

查看试题解析
17. 如图，已知函数y=x+b和y=ax+3的图象交点为P，则不等式x+b＞ax+3的解集为．

查看试题解析

三、解答题

18.

(1)、 $\sqrt{32} - (\sqrt{2} - 2 \sqrt{3}) (\sqrt{2} + 2 \sqrt{3})$ ；

(2)、 $(1 - \sqrt{5}) (\sqrt{5} + 1) + {(\sqrt{5} - 1)}^{2}$ ．

查看试题解析
19. 化简求值： $\frac{a^{2} - 1}{a^{2} - 2 a + 1} + \frac{2 a - a^{2}}{a - 2} \div a$ ，其中 $a = \sqrt{2} + 1$ ；

查看试题解析

20. 甲、乙两班各推选10名同学进行投篮比赛，按照比赛规则，每人各投了10个球，两个班选手的进球数统计如表，请根据表中数据解答下列问题

进球数/个	10	9	8	7	6	5
甲	1	1	1	4	0	3
乙	0	1	2	5	0	2

(1)、分别写出甲、乙两班选手进球数的平均数、中位数与众数；

(2)、如果要从这两个班中选出一个班级参加学校的投篮比赛，争取夺得总进球团体的第一名，你认为应该选择哪个班？如果要争取个人进球数进入学校前三名，你认为应该选择哪个班？

查看试题解析

21. 如图，折叠长方形一边AD，点D落在BC边的点F处，BC=10cm，AB=8cm，求：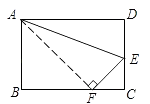

(1)、FC的长；

(2)、EF的长．

查看试题解析
22. 已知，直线y=2x+3与直线y=﹣2x﹣1.

(1)、求两直线与y轴交点A，B的坐标；

(2)、求两直线交点C的坐标；

(3)、求△ABC的面积.

查看试题解析
23. 某商店分两次购进A．B两种商品进行销售，两次购进同一种商品的进价相同，具体情况如下表所示：

(1)、求A、B两种商品每件的进价分别是多少元？

(2)、商场决定A种商品以每件30元出售，B种商品以每件100元出售．为满足市场需求，需购进A、B两种商品共1000件，且A种商品的数量不少于B种商品数量的4倍，请你求出获利最大的进货方案，并确定最大利润．

查看试题解析
24. 平面直角坐标系中，直线y=2kx-2k（k>0）交y轴于点B，与直线y=kx交于点A．

(1)、求点A的横坐标；

(2)、求出 $0 < 2 k x - 2 k < k x$ 的x的取值范围；

(3)、若P（0，3）求PA+OA的最小值，并求此时k的值；

(4)、若C（0，2）以A，B，C，D为顶点的四边形是以BC为一条边的菱形，求k的值．

查看试题解析

x	－2	0	1
y	3	p	0