山东省潍坊市潍城区2018-2019学年八年级下学期数学期末试卷
试卷更新日期:2020-06-23 类型:期末考试
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是A、
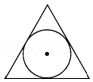 B、
B、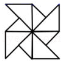 C、
C、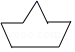 D、
D、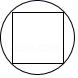 2. 一次函数 的图象可能是( )A、
2. 一次函数 的图象可能是( )A、 B、
B、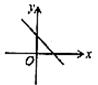 C、
C、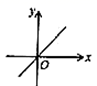 D、
D、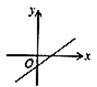 3. 通过估算,估计 的大小应在( )A、7~8之间 B、8.0~8.5之间 C、8.5~9.0之间 D、9~10之间4. 如图, 绕点 逆时针旋转 得到 ,若 , ,则 的度数是( )
3. 通过估算,估计 的大小应在( )A、7~8之间 B、8.0~8.5之间 C、8.5~9.0之间 D、9~10之间4. 如图, 绕点 逆时针旋转 得到 ,若 , ,则 的度数是( )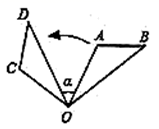 A、 B、 C、 D、5. 如图,四边形 和四边形 是以点 为位似中心的位似图形,若 ,四边形 的面积等于4,则四边形 的面积为( )
A、 B、 C、 D、5. 如图,四边形 和四边形 是以点 为位似中心的位似图形,若 ,四边形 的面积等于4,则四边形 的面积为( ) A、3 B、4 C、6 D、96. 如图,已知△ABC和△PBD都是正方形网格上的格点三角形(顶点为网格线的交点),要使ΔABC∽ΔPBD,则点P的位置应落在( )
A、3 B、4 C、6 D、96. 如图,已知△ABC和△PBD都是正方形网格上的格点三角形(顶点为网格线的交点),要使ΔABC∽ΔPBD,则点P的位置应落在( ) A、点上 B、点 上 C、点 上 D、点 上7. 在 中,点 为 的中点, 平分 ,且 于点 ,延长 交 于点 ,若 , ,则 的长为( )
A、点上 B、点 上 C、点 上 D、点 上7. 在 中,点 为 的中点, 平分 ,且 于点 ,延长 交 于点 ,若 , ,则 的长为( )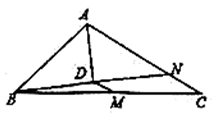 A、 B、1 C、 D、28. 如图所示,等边三角形 沿射线 向右平移到 的位置,连接 、 ,则下列结论:(1) (2) 与 互相平分(3)四边形 是菱形(4) ,其中正确的个数是( )
A、 B、1 C、 D、28. 如图所示,等边三角形 沿射线 向右平移到 的位置,连接 、 ,则下列结论:(1) (2) 与 互相平分(3)四边形 是菱形(4) ,其中正确的个数是( )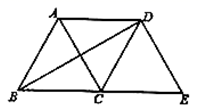 A、1 B、2 C、3 D、49. 如图,小明同学用自制的直角三角形纸板 测量树的高度 ,他调整自己的位置,设法使斜边 保持水平,并且边 与点 在同一直线上.已知纸板的两条直角边 , ,测得边 离地面的高度 , ,则树高 是( )
A、1 B、2 C、3 D、49. 如图,小明同学用自制的直角三角形纸板 测量树的高度 ,他调整自己的位置,设法使斜边 保持水平,并且边 与点 在同一直线上.已知纸板的两条直角边 , ,测得边 离地面的高度 , ,则树高 是( )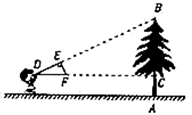 A、4米 B、4.5米 C、5米 D、5.5米10. 如图,在平面直角坐标系中,若点 在直线 与 轴正半轴、 轴正半轴围成的三角形内部,则 的值可能是( )
A、4米 B、4.5米 C、5米 D、5.5米10. 如图,在平面直角坐标系中,若点 在直线 与 轴正半轴、 轴正半轴围成的三角形内部,则 的值可能是( ) A、-3 B、3 C、4 D、511. 在一条笔直的航道上依次有甲、乙、丙三个港口,一艘船从甲出发,沿直线匀速行驶经过乙港驶向丙港,最终达到丙港,设行驶x (h)后,船与乙港的距离为y (km),y与x的关系如图所示,则下列说法正确的是( )
A、-3 B、3 C、4 D、511. 在一条笔直的航道上依次有甲、乙、丙三个港口,一艘船从甲出发,沿直线匀速行驶经过乙港驶向丙港,最终达到丙港,设行驶x (h)后,船与乙港的距离为y (km),y与x的关系如图所示,则下列说法正确的是( )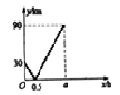 A、甲港与丙港的距离是90km B、船在中途休息了0.5小时 C、船的行驶速度是45km/h D、从乙港到达丙港共花了1.5小时12. 如图,在Rt△ABC中,AC=BC=2,将△ABC绕点A逆时针旋转60°,连接BD , 则图中阴影部分的面积是( )
A、甲港与丙港的距离是90km B、船在中途休息了0.5小时 C、船的行驶速度是45km/h D、从乙港到达丙港共花了1.5小时12. 如图,在Rt△ABC中,AC=BC=2,将△ABC绕点A逆时针旋转60°,连接BD , 则图中阴影部分的面积是( )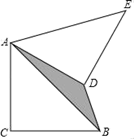 A、2 ﹣2 B、2 C、 ﹣1 D、4
A、2 ﹣2 B、2 C、 ﹣1 D、4二、填空题
-
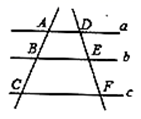
13. 使根式 有意义的x的取值范围是 .14. 如图,直线 ,直线 分别交 , , 于点 , , ,直线 分别交 , , 于点 , , .若 ,则 .
 15. 如图,已知函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),则根据图象可得不等式3x+b>ax﹣3的解集是.
15. 如图,已知函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),则根据图象可得不等式3x+b>ax﹣3的解集是.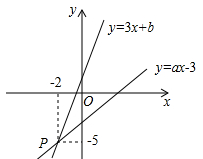 16. 如果关于x的不等式组 无解,则a的取值范围是.17. 如图,在平面直角坐标系中,已知 , , 是 轴上的一条动线段,且 ,当 取最小值时,点 坐标为.
16. 如果关于x的不等式组 无解,则a的取值范围是.17. 如图,在平面直角坐标系中,已知 , , 是 轴上的一条动线段,且 ,当 取最小值时,点 坐标为.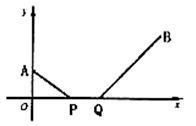 18. 如图,在直角坐标系中,已知点A(﹣3,0),B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2020的直角顶点的坐标为 .
18. 如图,在直角坐标系中,已知点A(﹣3,0),B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2020的直角顶点的坐标为 .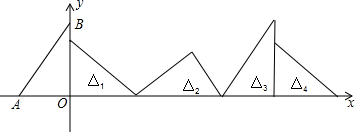
三、解答题
-
19.(1)、计算:(2)、计算:(3)、求不等式组 的整数解.20. 如图,方格纸中每个小正方形的边长都是1个单位长度, 的三个顶点 , , .
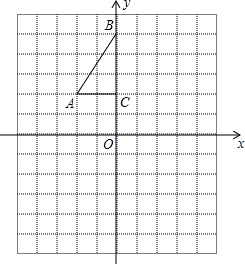 (1)、将 以点 为旋转中心旋转 ,得到△ ,请画出△ 的图形;(2)、平移 ,使点 的对应点 坐标为 ,请画出平移后对应的△ 的图形;(3)、若将△ 绕某一点旋转 可得到△ ,请直接写出旋转中心的坐标.21. 折叠矩形ABCD,使点D落在BC边上的点F处.
(1)、将 以点 为旋转中心旋转 ,得到△ ,请画出△ 的图形;(2)、平移 ,使点 的对应点 坐标为 ,请画出平移后对应的△ 的图形;(3)、若将△ 绕某一点旋转 可得到△ ,请直接写出旋转中心的坐标.21. 折叠矩形ABCD,使点D落在BC边上的点F处.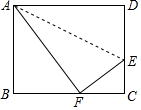 (1)、求证:△ABF∽△FCE;(2)、若DC=8,CF=4,求矩形ABCD的面积S.22. 如图,直线 分别与 轴、 轴交于点 , ;直线 分别与 轴交于点 ,与直线 交于点 ,已知关于 的不等式 的解集是 .
(1)、求证:△ABF∽△FCE;(2)、若DC=8,CF=4,求矩形ABCD的面积S.22. 如图,直线 分别与 轴、 轴交于点 , ;直线 分别与 轴交于点 ,与直线 交于点 ,已知关于 的不等式 的解集是 . (1)、分别求出 , , 的值;(2)、求 .23. 如图,四边形 中, ,将 绕点 顺时针旋转一定角度后,点 的对应点恰好与点 重合,得到 .
(1)、分别求出 , , 的值;(2)、求 .23. 如图,四边形 中, ,将 绕点 顺时针旋转一定角度后,点 的对应点恰好与点 重合,得到 .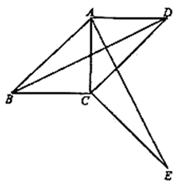 (1)、判断 的形状,并说明理由;(2)、若 , ,试求出四边形 的对角线 的长.24. 我市某风景区门票价格如图所示,有甲、乙两个旅行团队,计划在端午节期间到该景点游玩,两团队游客人数之和为100人,乙团队人数不超过40人.设甲团队人数为 人,如果甲、乙两团队分别购买门票,两团队门票款之和为 元.
(1)、判断 的形状,并说明理由;(2)、若 , ,试求出四边形 的对角线 的长.24. 我市某风景区门票价格如图所示,有甲、乙两个旅行团队,计划在端午节期间到该景点游玩,两团队游客人数之和为100人,乙团队人数不超过40人.设甲团队人数为 人,如果甲、乙两团队分别购买门票,两团队门票款之和为 元.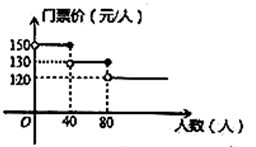 (1)、求出 关于 的函数关系式,并写出自变 的取值范围;(2)、若甲团队人数不超过80人,计算甲、乙两团队联合购票比分别购票最多可节约多少钱?(3)、端午节之后,该风景区对门票价格作了如下调整:人数不超过40人时,门票价格不变,人数超过40人但不超过80人时,每张门票降价 元;人数超过80人时,每张门票降价 元.在(2)的条件下,若甲、乙两个旅行团端午节之后去游玩联合购票比分别购票最多可节约3900元,求 的值.
(1)、求出 关于 的函数关系式,并写出自变 的取值范围;(2)、若甲团队人数不超过80人,计算甲、乙两团队联合购票比分别购票最多可节约多少钱?(3)、端午节之后,该风景区对门票价格作了如下调整:人数不超过40人时,门票价格不变,人数超过40人但不超过80人时,每张门票降价 元;人数超过80人时,每张门票降价 元.在(2)的条件下,若甲、乙两个旅行团端午节之后去游玩联合购票比分别购票最多可节约3900元,求 的值.