江苏省南通市启东市2020年数学中考一模试卷

试卷更新日期：2020-06-23 类型：中考模拟

进入出卷网下载

一、选择题

1. 关于代数式x＋2的结果，下列说法一定正确的是（）

A、比2大 B、比2小 C、比x大 D、比x小

查看试题解析
2. 将一个直角三角板和一把直尺如图放置，如果∠α=43°，则∠β的度数是（）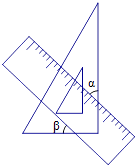

A、43° B、47° C、30° D、60°

查看试题解析
3. 下列图标，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 某篮球兴趣小组7名学生参加投篮比赛，每人投10个，投中的个数分别为：8，5，7，5，8，6，8，则这组数据的众数和中位数分别为（）

A、5，7 B、6，7 C、8，5 D、8，7

查看试题解析
5. 已知x₁ ， x₂是一元二次方程x²+x﹣3＝0的两个根，则x₁+x₂﹣x₁x₂的值为（　　）

A、1 B、2 C、3 D、4

查看试题解析
6. 若一次函数 $y = k x + b$ ，当 $x$ 得值减小1， $y$ 的值就减小2，则当 $x$ 的值增加2时， $y$ 的值（）

A、增加4 B、减小4 C、增加2 D、减小2

查看试题解析
7. 用一个圆心角为120°，半径为6的扇形作一个圆锥的侧面，则这个圆锥的底面半径为（　　）

A、1 B、2 C、3 D、6

查看试题解析
8. 若关于x的不等式组 ${\begin{matrix} 2 x + 7 > 4 x + 1 \\ x - k < 2 \end{matrix}$ 的解集为x＜3，则k的取值范围为（）

A、k＞1 B、k＜1 C、k≥1 D、k≤1

查看试题解析
9. 二次函数y₁＝ax²＋bx＋c（a，b，c为常数）的图象如图所示，若y₁＋y₂＝2，则下列关于函数y₂的图象与性质描述正确的是（）

A、函数y₂的图象开口向上 B、函数y₂的图象与x轴没有公共点 C、当x＞2时，y₂随x的增大而减小 D、当x＝1时，函数y₂的值小于0

查看试题解析
10. 如图，在△ABC中，BC＞AB＞AC，D是边BC上的一个动点（点D不与点B、C重合），将△ABC沿AD折叠，点B落在点B'处，连接BB'，B'C，若△BCB'是等腰三角形，则符合条件的点D的个数是

A、0个 B、1个 C、2个 D、3个

查看试题解析

二、填空题

11. 保护水资源，人人有责．我国是缺水国家，目前可利用淡水资源总量仅约为899000亿m³ ，数据899000用科学记数法表示为．

查看试题解析
12. 计算： $\frac{4}{\sqrt{2}}$ ﹣ $\sqrt{8}$ ＝.

查看试题解析
13. 分解因式：a³﹣2a²+a= ．

查看试题解析
14. 如图，在矩形ABCD中，E是CD的延长线上一点，连接BE交AD于点F.如果AB=4，BC=6，DE=3，那么AF的长为.

查看试题解析
15. 《算法统宗》是中国古代数学名著，作者是明代著名数学家程大位．在其中有这样的记载“一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁？”译文：有100名和尚分100个馒头，正好分完．如果大和尚一人分3个，小和尚3人分一个，试问大、小和尚各有几人？设有大和尚x人，小和尚y人，可列方程组为．

查看试题解析
16. 如图，AB是⊙O的弦，半径OC⊥AB，AC∥OB，则∠BOC的度数为.

查看试题解析
17. 如图，点A在反比例函数 $y_{1} = \frac{1}{x} (x > 0)$ 的图象上，点B在反比例函数 $y_{2} = \frac{k}{x} (x < 0)$ 的图象上，AB⊥y轴，若△AOB的面积为2，则k的值为.

查看试题解析
18. 如图，线段AB＝4，M为AB的中点，动点P到点M的距离是1，连接PB，线段PB绕点P逆时针旋转90°得到线段PC，连接AC，则线段AC长度的最大值是．

查看试题解析

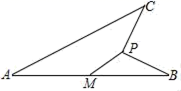
三、解答题

19.

(1)、计算：（﹣1）³+|﹣6|×2^﹣¹﹣ $\sqrt[3]{27}$ ；

(2)、解不等式：x $- \frac{x + 2}{2}$ ＜ $\frac{2 - x}{3}$ ，并把解集在数轴上表示出来.

查看试题解析
20.

(1)、先化简，再求值：（1﹣ $\frac{1}{m + 2}$ ）÷ $\frac{m^{2} + 2 m + 1}{m^{2} - 4}$ ，其中m＝1；

(2)、解方程： $\frac{1}{x - 3}$ ＝3+ $\frac{x}{3 - x}$ .

查看试题解析
21.
如图，点A，B，C，D在同一条直线上，CE∥DF，EC=BD，AC=FD．求证：AE=FB．

查看试题解析
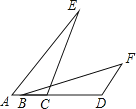22. 某市体育中考现场考试内容有三项：50米跑为必测项目.另在立定跳远、实心球（二选一）和坐位体前屈、1分钟跳绳（二选一）中选择两项.

(1)、每位考生有种选择方案；

(2)、求小明与小刚选择同种方案的概率.

查看试题解析
23. 如图，兰兰站在河岸上的G点，看见河里有一只小船沿垂直于岸边的方向划过来，此时，测得小船C的俯角是∠FDC＝30°，若兰兰的眼睛与地面的距离是1.5米，BG＝1米，BG平行于AC所在的直线，迎水坡的坡度i＝4：3，坡高BE＝8米，求小船C到岸边的距离CA的长.（参考数据： $\sqrt{3}$ ≈1.7，结果保留一位小数）

查看试题解析
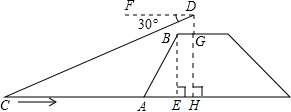24. 在平面直角坐标系 $x O y$ 中，抛物线 $y = a x^{2} - 2 a x - 3 a_{_{}} {_{}}^{} (a \neq 0)$ ，与x轴交于A、B两点(点A在点B的左侧).

(1)、求点A和点B的坐标；

(2)、若点P（m，n）是抛物线上的一点，过点P作x轴的垂线，垂足为点D.
①在 $a > 0$ 的条件下，当 $- 2 \leq m \leq 2$ 时，n的取值范围是 $- 4 \leq n \leq 5$ ，求抛物线的表达式；

②若D点坐标（4，0），当 $P D > A D$ 时，求a的取值范围.

查看试题解析
25. 如图，已知矩形ABCD中，AB＝4，动点P从点A出发，沿AD方向以每秒1个单位的速度运动，连接BP，作点A关于直线BP的对称点E，设点P的运动时间为t（s）.

(1)、若AD＝6，P仅在边AD运动，求当P，E，C三点在同一直线上时对应的t的值.

(2)、在动点P在射线AD上运动的过程中，求使点E到直线BC的距离等于3时对应的t的值.

查看试题解析
26. 定义：当点P在射线OA上时，把 $\frac{O P}{O A}$ 的的值叫做点P在射线OA上的射影值；当点P不在射线OA上时，把射线OA上与点P最近点的射影值，叫做点P在射线OA上的射影值.
例如：如图1，△OAB三个顶点均在格点上，BP是OA边上的高，则点P和点B在射线OA上的射影值均为 $\frac{O P}{O A}$ ＝ $\frac{1}{3}$ .

(1)、在△OAB中，
①点B在射线OA上的射影值小于1时，则△OAB是锐角三角形；

②点B在射线OA上的射影值等于1时，则△OAB是直角三角形；

③点B在射线OA上的射影值大于1时，则△OAB是钝角三角形.

其中真命题有　　.

A、①② B、①③ C、②③ D、①②③

(2)、已知：点C是射线OA上一点，CA＝OA＝1，以〇为圆心，OA为半径画圆，点B是⊙O上任意点.
①如图2，若点B在射线OA上的射影值为 $\frac{1}{2}$ .求证：直线BC是⊙O的切线；

②如图3，已知D为线段BC的中点，设点D在射线OA上的射影值为x，点D在射线OB上的射影值为y，直接写出y与x之间的函数关系式为.

查看试题解析