江苏省南京市联合体2020年数学中考一模试卷
试卷更新日期:2020-06-23 类型:中考模拟
一、选择题
-
1. 4的算术平方根是( )A、 2 B、-2 C、±2 D、±22. 2019年江苏省粮食总产达40 540 000吨,居全国第四位.用科学记数法表示40 540 000是( )A、 4054×104 B、4.054×104 C、4.054×107 D、4054×1073.
计算 的结果是( )
A、 B、 C、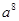 D、
D、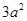 4. 已知△ABC∽△DEF,△ABC与△DEF面积之比为1
4. 已知△ABC∽△DEF,△ABC与△DEF面积之比为1 4.若BC=1,则EF的长是( ) A、2 B、2 C、4 D、165. 下列整数中,与7- 最接近的是( )A、1 B、2 C、3 D、46. 已知一次函数y=kx+b的图象如图所示,则y=-2kx-b的图象可能是( )
4.若BC=1,则EF的长是( ) A、2 B、2 C、4 D、165. 下列整数中,与7- 最接近的是( )A、1 B、2 C、3 D、46. 已知一次函数y=kx+b的图象如图所示,则y=-2kx-b的图象可能是( )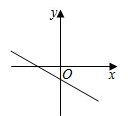 A、
A、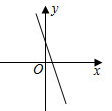 B、
B、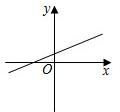 C、
C、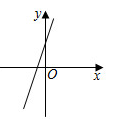 D、
D、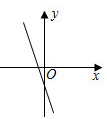
二、填空题
-
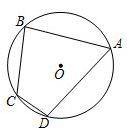
7. 使式子1+ 有意义的x的取值范围是.8. 计算 的结果是.9. 分解因式a(a-1)-a+1的结果是.10. 已知1是关于x的方程x2+mx-3=0的一个根,则另一个根为 , m=.11. 若一组数据 2,3,4,5,x 的方差比另一组数据 5,6,7,8,9 的方差小,则 x 可以为.(例举一个满足条件的值)12. 如图,四边形ABCD是⊙O的内接四边形,若⊙O半径为4,且∠C=2∠A,则 的长为.
 13. 如图,将正六边形ABCDEF绕点D逆时针旋转27°得正六边形A′B′C′DE′F′,则∠1=°.
13. 如图,将正六边形ABCDEF绕点D逆时针旋转27°得正六边形A′B′C′DE′F′,则∠1=°.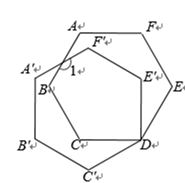 14. 反比例函数y= 的图像过点(-2,a)、(2,b),若a-b=-6,则ab=.15. 如图,在Rt△ACB中,∠C=90°,BC=4,AB=5,BD平分∠ABC交AC于点D,则AD=.
14. 反比例函数y= 的图像过点(-2,a)、(2,b),若a-b=-6,则ab=.15. 如图,在Rt△ACB中,∠C=90°,BC=4,AB=5,BD平分∠ABC交AC于点D,则AD=.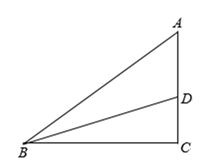 16. 如图,在平面直角坐标系中,点A的坐标是(2,1),点B的坐标是(2,0) .作点B关于OA的对称点B′,则点B′的坐标是.
16. 如图,在平面直角坐标系中,点A的坐标是(2,1),点B的坐标是(2,0) .作点B关于OA的对称点B′,则点B′的坐标是.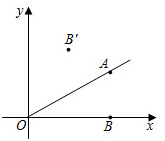
三、解答题
-
17. 计算 .18. 解不等式组 ,并把解集在数轴上表示出来.19. 课外兴趣小组为了解某段路上机动车的车速,抽查了一段时间内若干辆车的车速(车速取整数,单位:千米/时)并制成如图所示的频数分布直方图.已知车速在41千米/时到50千米/时的车辆数占车辆总数的 .
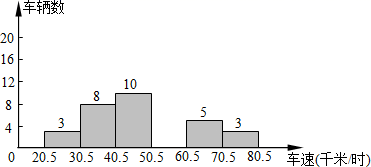 (1)、在这段时间内他们抽查的车有辆;(2)、被抽查车辆的车速的中位数所在速度段(单位:千米/时)是( )A、30.5~40.5 B、40.5~50.5 C、50.5~60.5 D、60.5~70.5(3)、补全频数分布直方图;(4)、如果全天超速(车速大于60千米/时)的车有200辆,则当天的车流量约为多少辆?20. 甲、乙、丙3名医生志愿报名参加新冠肺炎救治工作.(1)、随机抽取1名,则恰是甲的概率是;(2)、随机抽取2名,求甲在其中的概率.21. 现有120台大小两种型号的挖掘机同时工作,大型挖掘机每小时可挖掘土方360立方米,小型挖掘机每小时可挖掘土方200立方米,20小时共挖掘土方704 000立方米,求大小型号的挖掘机各多少台?22. 一辆货车从A地出发以每小时80km的速度匀速驶往B地,一段时间后,一辆轿车从B地出发沿同一条路匀速驶往A地.货车行驶3小时后,在距B地160km处与轿车相遇.图中线段表示货车离B地的距离y1与货车行驶的时间x的关系.
(1)、在这段时间内他们抽查的车有辆;(2)、被抽查车辆的车速的中位数所在速度段(单位:千米/时)是( )A、30.5~40.5 B、40.5~50.5 C、50.5~60.5 D、60.5~70.5(3)、补全频数分布直方图;(4)、如果全天超速(车速大于60千米/时)的车有200辆,则当天的车流量约为多少辆?20. 甲、乙、丙3名医生志愿报名参加新冠肺炎救治工作.(1)、随机抽取1名,则恰是甲的概率是;(2)、随机抽取2名,求甲在其中的概率.21. 现有120台大小两种型号的挖掘机同时工作,大型挖掘机每小时可挖掘土方360立方米,小型挖掘机每小时可挖掘土方200立方米,20小时共挖掘土方704 000立方米,求大小型号的挖掘机各多少台?22. 一辆货车从A地出发以每小时80km的速度匀速驶往B地,一段时间后,一辆轿车从B地出发沿同一条路匀速驶往A地.货车行驶3小时后,在距B地160km处与轿车相遇.图中线段表示货车离B地的距离y1与货车行驶的时间x的关系.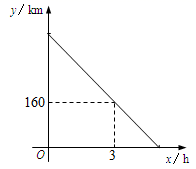 (1)、AB两地之间的距离为km;(2)、求y1与x之间的函数关系式;(3)、若两车同时到达各自目的地,在同一坐标系中画出轿车离B地的距离y2与货车行驶时间x的函数图象,用文字说明该图像与x轴交点所表示的实际意义.23.(1)、如图①,在四边形ABCD中,∠A=∠C=90°,AB=CD,求证:四边形ABCD是矩形;(2)、如图②,若四边形ABCD满足∠A=∠C>90°,AB=CD,求证:四边形ABCD是平行四边形.
(1)、AB两地之间的距离为km;(2)、求y1与x之间的函数关系式;(3)、若两车同时到达各自目的地,在同一坐标系中画出轿车离B地的距离y2与货车行驶时间x的函数图象,用文字说明该图像与x轴交点所表示的实际意义.23.(1)、如图①,在四边形ABCD中,∠A=∠C=90°,AB=CD,求证:四边形ABCD是矩形;(2)、如图②,若四边形ABCD满足∠A=∠C>90°,AB=CD,求证:四边形ABCD是平行四边形.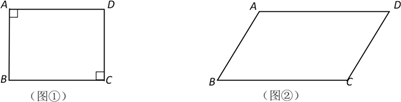 24. 如图,B位于A南偏西37°方向, 港口C位于A南偏东35°方向,B位于C正西方向. 轮船甲从A出发沿正南方向行驶40海里到达点D处,此时轮船乙从B出发沿正东方向行驶20海里至E处,E位于D南偏西45°方向.这时,E处距离港口C有多远? (参考数据:tan37°≈0.75,tan35°≈0.70)
24. 如图,B位于A南偏西37°方向, 港口C位于A南偏东35°方向,B位于C正西方向. 轮船甲从A出发沿正南方向行驶40海里到达点D处,此时轮船乙从B出发沿正东方向行驶20海里至E处,E位于D南偏西45°方向.这时,E处距离港口C有多远? (参考数据:tan37°≈0.75,tan35°≈0.70) 25. 如图①,在矩形ABCD中,AB=6,BC=9,点E是BC边上一动点,连接AE、DE ,作△ECD的外接⊙O,交AD于点F,交AE于点G,连接FG.
25. 如图①,在矩形ABCD中,AB=6,BC=9,点E是BC边上一动点,连接AE、DE ,作△ECD的外接⊙O,交AD于点F,交AE于点G,连接FG.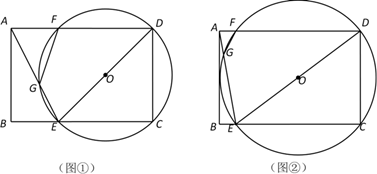 (1)、求证△AFG∽△AED;(2)、当BE的长为时,△AFG为等腰三角形;(3)、如图②,若BE=1,求证:AB与⊙O相切.26. 已知二次函数y=x2-2mx+m2+m-1(m是常数).(1)、求证:不论m为何值,该函数的图象的顶点都在函数y=x-1的图像上.(2)、若该函数的图象与函数y=x+b的图像有两个交点,则b的取值范围为( )A、b>0 B、b>-1 C、b>- D、b>-2(3)、该函数图象与坐标轴交点的个数随m的值变化而变化,直接写出交点个数及对应的m的取值范围.27. (概念认识)
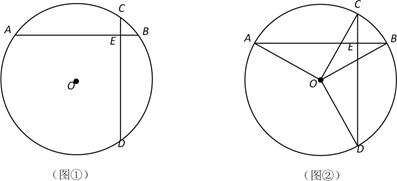
(1)、求证△AFG∽△AED;(2)、当BE的长为时,△AFG为等腰三角形;(3)、如图②,若BE=1,求证:AB与⊙O相切.26. 已知二次函数y=x2-2mx+m2+m-1(m是常数).(1)、求证:不论m为何值,该函数的图象的顶点都在函数y=x-1的图像上.(2)、若该函数的图象与函数y=x+b的图像有两个交点,则b的取值范围为( )A、b>0 B、b>-1 C、b>- D、b>-2(3)、该函数图象与坐标轴交点的个数随m的值变化而变化,直接写出交点个数及对应的m的取值范围.27. (概念认识)在同一个圆中两条互相垂直且相等的弦定义为“等垂弦”,两条弦所在直线的交点为等垂弦的分割点.如图①,AB、CD是⊙O的弦,AB=CD,AB⊥CD,垂足为E,则AB、CD是等垂弦,E为等垂弦AB、CD的分割点.
 (1)、(数学理解)
(1)、(数学理解)如图②,AB是⊙O的弦,作OC⊥OA、OD⊥OB,分别交⊙O于点C、D,连接CD.求证: AB、CD是⊙O的等垂弦.
(2)、在⊙O中,⊙O的半径为5,E为等垂弦AB、CD的分割点, .求AB的长度.(3)、(问题解决)AB、CD是⊙O的两条弦,CD= AB,且CD⊥AB,垂足为F.
①在图③中,利用直尺和圆规作弦CD(保留作图痕迹,不写作法).
②若⊙O的半径为r,AB=mr(m为常数),垂足F与⊙O的位置关系随m的值变化而变化,直接写出点F与⊙O的位置关系及对应的m的取值范围.
