湖北省武汉市2020年数学中考模拟试卷(4月)
试卷更新日期:2020-06-23 类型:中考模拟
一、选择题
-
1. 的绝对值是( )A、 B、 C、 D、2. 若 在实数范围内有意义,则x的取值范围是( )A、x大于5 B、x≥5 C、x≤5 D、x≠53. “投掷一枚硬币,正面朝上”这一事件是( )A、必然事件 B、随机事件 C、不可能事件 D、确定事件4. 下列电动车品牌标志中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 下列几何体中,俯视图为三角形的是( )A、
5. 下列几何体中,俯视图为三角形的是( )A、 B、
B、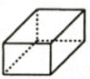 C、
C、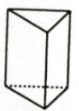 D、
D、 6. 小明乘车从甲地到乙地,行车的速度v(km/h)和行车时间t(h)之间的函数图象是( )A、
6. 小明乘车从甲地到乙地,行车的速度v(km/h)和行车时间t(h)之间的函数图象是( )A、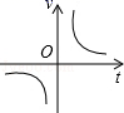 B、
B、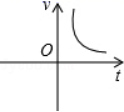 C、
C、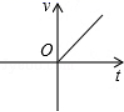 D、
D、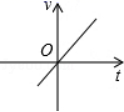 7. 在一只不透明的口袋中放入只有颜色不同的白球6个,黑球8个,黄球n个,搅匀后随机从中摸取一个恰好是黄球的概率为 ,则放入的黄球个数n=( )A、4 B、5 C、6 D、78. 如图,在平面直角坐标系中,点P(2,5)、Q(a,b)(a>2)在“函数y= (x>0)的图象上,过点P分别作x轴、y轴的垂线,垂足为A,B;过点Q分别作x轴、y轴的垂线,垂足为C,D,QD交PA于点E,随着a的增大,四边形ACQE的面积( )
7. 在一只不透明的口袋中放入只有颜色不同的白球6个,黑球8个,黄球n个,搅匀后随机从中摸取一个恰好是黄球的概率为 ,则放入的黄球个数n=( )A、4 B、5 C、6 D、78. 如图,在平面直角坐标系中,点P(2,5)、Q(a,b)(a>2)在“函数y= (x>0)的图象上,过点P分别作x轴、y轴的垂线,垂足为A,B;过点Q分别作x轴、y轴的垂线,垂足为C,D,QD交PA于点E,随着a的增大,四边形ACQE的面积( ) A、增大 B、减小 C、先减小后增大 D、先增大后减小9. 如图所示,A1(1, ),A2( , ),A3(2, ),A4(3,0).作折线A1A2A3A4关于点A4的中心对称图形,再做出新的折线关于与x轴的下一个交点的中心对称图形……以此类推,得到一个大的折线.现有一动点P从原点O出发,沿着折线一每秒1个单位的速度移动,设运动时间为t.当t=2020时,点P的坐标为( )
A、增大 B、减小 C、先减小后增大 D、先增大后减小9. 如图所示,A1(1, ),A2( , ),A3(2, ),A4(3,0).作折线A1A2A3A4关于点A4的中心对称图形,再做出新的折线关于与x轴的下一个交点的中心对称图形……以此类推,得到一个大的折线.现有一动点P从原点O出发,沿着折线一每秒1个单位的速度移动,设运动时间为t.当t=2020时,点P的坐标为( ) A、(1010, ) B、(2020, ) C、(2016,0) D、(1010, )10. 如图,D是等腰△ABC外接圆弧AC上的点,AB=AC且∠CAB=56°,则∠ADC的度数为( )
A、(1010, ) B、(2020, ) C、(2016,0) D、(1010, )10. 如图,D是等腰△ABC外接圆弧AC上的点,AB=AC且∠CAB=56°,则∠ADC的度数为( )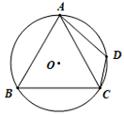 A、116° B、118° C、122° D、126°
A、116° B、118° C、122° D、126°二、填空题
-
11. 计算 .12. 计算 的结果是13. 如图是甲、乙两名射击运动员10次射击成绩的统计表和折线统计图.
平均数
中位数
众数
甲
8
8
8
乙
8
8
8
你认为甲、乙两名运动员,的射击成绩更稳定.(填甲或乙)
 14. 如图,在▱ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是(把所有正确结论的序号部填在横线上).①∠AEF= ∠DFE;②S△BEC=2S△CEF;③EF=CF;④∠BCD=2∠DCF.
14. 如图,在▱ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是(把所有正确结论的序号部填在横线上).①∠AEF= ∠DFE;②S△BEC=2S△CEF;③EF=CF;④∠BCD=2∠DCF. 15. 抛物线y=x2﹣2x﹣3的顶点坐标是.16. 已知:如图,四边形ABCD中,AD∥BC,AB=BC=4,∠B=60°,∠C=105°,点E为BC的中点,以CE为弦作圆,设该圆与四边形ABCD的一边的交点为P,若∠CPE=30°,则EP的长为.
15. 抛物线y=x2﹣2x﹣3的顶点坐标是.16. 已知:如图,四边形ABCD中,AD∥BC,AB=BC=4,∠B=60°,∠C=105°,点E为BC的中点,以CE为弦作圆,设该圆与四边形ABCD的一边的交点为P,若∠CPE=30°,则EP的长为.
三、解答题
-
17. 计算:(﹣a2)3+a2•a3+a8÷(﹣a2)18. 如图,要在长方形钢板ABCD的边AB上找一点E,使∠AEC=150°,应怎样确定点E的位置?为什么?
 19. 中华文明,源远流长,中华汉字,寓意深广。为传承中华优秀传统文化,某中学德育处组织了一次全校2000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,学校德育处随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
19. 中华文明,源远流长,中华汉字,寓意深广。为传承中华优秀传统文化,某中学德育处组织了一次全校2000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,学校德育处随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:成绩x(分)分数段
频数(人)
频率
50≤x<60
10
0.05
60≤x<70
30
0.15
70≤x<80
40
0.2
80≤x<90
m
0.35
90≤x<100
50
n
频数分布直方图

根据所给的信息,回答下列问题:
(1)、m=;n=;(2)、补全频数分布直方图;(3)、这200名学生成绩的中位数会落在分数段;(4)、若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的2000名学生中成绩是“优”等的约有多少人?20. 如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点.△ABC的顶点在格点上,A(1,0)、C(0,7). (1)、在方格纸中画出平面直角坐标系,写出B点的坐标:B;(2)、直接写出△ABC的形状: , 直接写出△ABC的面积;(3)、若D(﹣1,4),连接BD交AC于E,则 =.21. 如图,已知直线AB经过⊙O上的点C,并且OA=OB,CA=CB.
(1)、在方格纸中画出平面直角坐标系,写出B点的坐标:B;(2)、直接写出△ABC的形状: , 直接写出△ABC的面积;(3)、若D(﹣1,4),连接BD交AC于E,则 =.21. 如图,已知直线AB经过⊙O上的点C,并且OA=OB,CA=CB. (1)、求证:直线AB是⊙O的切线;(2)、OA,OB分别交⊙O于点D,E,AO的延长线交⊙O于点F,若AB=4AD,求sin∠CFE的值.22. 为迎接“五一”国际劳动节,某商场计划购进甲、乙两种品牌的 恤衫共100件,已知乙品牌每件的进价比甲品牌每件的进价贵30元,且用120元购买甲品牌的件数恰好是购买乙品牌件数的2倍.(1)、求甲、乙两种品牌每件的进价分别是多少元?(2)、商场决定甲品牌以每件50元出售,乙品牌以每件100元出售.为满足市场需求,购进甲种品牌的数量不少于乙种品牌数量的4倍,请你确定获利最大的进货方案,并求出最大利润.23. 定义:连结菱形的一边中点与对边的两端点的线段把它分成三个三角形,如果其中有两个三角形相似,那么称这样的菱形为自相似菱形.
(1)、求证:直线AB是⊙O的切线;(2)、OA,OB分别交⊙O于点D,E,AO的延长线交⊙O于点F,若AB=4AD,求sin∠CFE的值.22. 为迎接“五一”国际劳动节,某商场计划购进甲、乙两种品牌的 恤衫共100件,已知乙品牌每件的进价比甲品牌每件的进价贵30元,且用120元购买甲品牌的件数恰好是购买乙品牌件数的2倍.(1)、求甲、乙两种品牌每件的进价分别是多少元?(2)、商场决定甲品牌以每件50元出售,乙品牌以每件100元出售.为满足市场需求,购进甲种品牌的数量不少于乙种品牌数量的4倍,请你确定获利最大的进货方案,并求出最大利润.23. 定义:连结菱形的一边中点与对边的两端点的线段把它分成三个三角形,如果其中有两个三角形相似,那么称这样的菱形为自相似菱形. (1)、判断下列命题是真命题,还是假命题?
(1)、判断下列命题是真命题,还是假命题?①正方形是自相似菱形;
②有一个内角为60°的菱形是自相似菱形.
③如图1,若菱形ABCD是自相似菱形,∠ABC=α(0°<α<90°),E为BC中点,则在△ABE,△AED,△EDC中,相似的三角形只有△ABE与△AED.
(2)、如图2,菱形ABCD是自相似菱形,∠ABC是锐角,边长为4,E为BC中点.①求AE,DE的长;
②AC,BD交于点O,求tan∠DBC的值.
24. 已知抛物线y=x2+bx+c与x轴交于点A(4,﹣5). (1)、如图,过点A分别向x轴、y轴作垂线,垂足分别为B、C,得到矩形ABOC,且抛物线经过点C.
(1)、如图,过点A分别向x轴、y轴作垂线,垂足分别为B、C,得到矩形ABOC,且抛物线经过点C.①求抛物线的解析式.
②将抛物线沿直线x=m(2>m>0)翻折,分别交线段OB、AC于D,E两点.若直线DE刚好平分矩形ABOC的面积,求m的值.
(2)、将抛物线旋转180°,使点A的对应点为A1(m﹣2,n﹣4),其中m≤2.若旋转后的抛物线仍然经过点A,求旋转后的抛物线顶点所能达到最低点时的坐标.