河南省商丘市柘城县2020年数学中考模拟试卷
试卷更新日期:2020-06-23 类型:中考模拟
一、选择题
-
1. sin30°的值为( )A、 B、 C、 D、2. 下列函数中,y是x的反比例函数的是( )
A、 B、 C、y=3x D、y=x23.如图,几何体的俯视图是( )
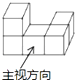 A、
A、 B、
B、 C、
C、 D、
D、 4. 某游戏的规则为:选手蒙眼在一张如图所示的正方形黑白格子纸(九个小正方形面积相等)上描一个点,若所描的点落在黑色区域,获得笔记本一个;若落在白色区域,获得钢笔一支.选手获得笔记本的概率为( )
4. 某游戏的规则为:选手蒙眼在一张如图所示的正方形黑白格子纸(九个小正方形面积相等)上描一个点,若所描的点落在黑色区域,获得笔记本一个;若落在白色区域,获得钢笔一支.选手获得笔记本的概率为( ) A、 B、 C、 D、5. 若△ABC~△DEF,相似比为3:2,则对应高的比为( )A、3:2 B、3:5 C、9:4 D、4:96. 一元二次方程 的根的情况是( )A、没有实数根 B、有两个相等的实数根 C、只有一个实数根 D、有两个不相等的实数根7. 如图,圆O是△ABC的外接圆,∠A=68°,则∠BOC的大小是( )
A、 B、 C、 D、5. 若△ABC~△DEF,相似比为3:2,则对应高的比为( )A、3:2 B、3:5 C、9:4 D、4:96. 一元二次方程 的根的情况是( )A、没有实数根 B、有两个相等的实数根 C、只有一个实数根 D、有两个不相等的实数根7. 如图,圆O是△ABC的外接圆,∠A=68°,则∠BOC的大小是( )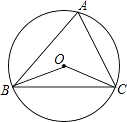 A、22° B、32° C、136° D、68°8.
A、22° B、32° C、136° D、68°8.图1和图2中所有的正方形都全等,将图1的正方形放在图2中的①②③④某一位置,所组成的图形不能围成正方体的位置是( )
 A、① B、② C、③ D、④9. 已知菱形 在平面直角坐标系的位置如图所示,顶点 , ,点 是对角线 上的一个动点, , 当 最短时,点 的坐标为( )
A、① B、② C、③ D、④9. 已知菱形 在平面直角坐标系的位置如图所示,顶点 , ,点 是对角线 上的一个动点, , 当 最短时,点 的坐标为( ) A、 B、 C、 D、10. 已知二次函数 (a≠0)的图象的顶点在第四象限,且过点(﹣1,0),当a﹣b为整数时,ab的值为( )A、 或1 B、 或1 C、 或 D、 或
A、 B、 C、 D、10. 已知二次函数 (a≠0)的图象的顶点在第四象限,且过点(﹣1,0),当a﹣b为整数时,ab的值为( )A、 或1 B、 或1 C、 或 D、 或二、填空题
-
11. 在 中, , , ,则 .12. 若函数 是关于x的反比例函数,则m的值是13. 如图, 中, , , ,将 绕点 逆时针旋转得到 , 与 相交于点 ,当 时, .
 14. 如图,在矩形ABCD中,AD=2,以点A为圆心,AD长为半径画弧,交BC边于点E , 若E恰为BC的中点,则图中阴影部分的面积为 .
14. 如图,在矩形ABCD中,AD=2,以点A为圆心,AD长为半径画弧,交BC边于点E , 若E恰为BC的中点,则图中阴影部分的面积为 .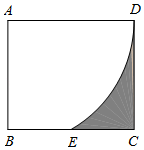 15. 如图,等腰 中, , ,点 是边 上不与点 , 重合的一个动点,直线 垂直平分 ,垂足为 ,当 是直角三角形时, 的长为.
15. 如图,等腰 中, , ,点 是边 上不与点 , 重合的一个动点,直线 垂直平分 ,垂足为 ,当 是直角三角形时, 的长为. 16.(1)、计算:(2)、解方程:17. 如图,在 中, , ,垂足分别为 , , 与 相交于点 .
16.(1)、计算:(2)、解方程:17. 如图,在 中, , ,垂足分别为 , , 与 相交于点 . (1)、求证: ;(2)、当 , 时,求 的长.18. 如图,转盘A的三个扇形面积相等,分别标有数字1,2,3,转盘B的四个扇形面积相等,分别有数字1,2,3,4.转动A、B转盘各一次,当转盘停止转动时,将指针所落扇形中的两个数字相乘(当指针落在四个扇形的交线上时,重新转动转盘).
(1)、求证: ;(2)、当 , 时,求 的长.18. 如图,转盘A的三个扇形面积相等,分别标有数字1,2,3,转盘B的四个扇形面积相等,分别有数字1,2,3,4.转动A、B转盘各一次,当转盘停止转动时,将指针所落扇形中的两个数字相乘(当指针落在四个扇形的交线上时,重新转动转盘).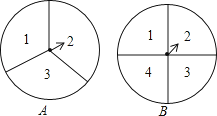 (1)、用树状图或列表法列出所有可能出现的结果;(2)、求两个数字的积为奇数的概率.19. 如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有25米的距离(B,F,C在一条直线上).
(1)、用树状图或列表法列出所有可能出现的结果;(2)、求两个数字的积为奇数的概率.19. 如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有25米的距离(B,F,C在一条直线上).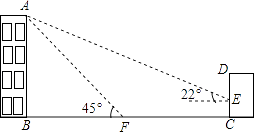 (1)、求办公楼AB的高度;
(1)、求办公楼AB的高度;
(2)、若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.(参考数据:sin22°≈ ,cos22° ,tan22 )
20. 如图,△ABC是⊙O的内接三角形,AB为直径,过点B的切线与AC的延长线交于点D,E是BD中点,连接CE. (1)、求证:CE是⊙O的切线;(2)、若AC=4,BC=2,求BD和CE的长.21. 如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点D、M分别在边AB、OA上,且AD=2DB,AM=2MO,一次函数y=kx+b的图象过点D和M,反比例函数y= 的图象经过点D,与BC的交点为N.
(1)、求证:CE是⊙O的切线;(2)、若AC=4,BC=2,求BD和CE的长.21. 如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点D、M分别在边AB、OA上,且AD=2DB,AM=2MO,一次函数y=kx+b的图象过点D和M,反比例函数y= 的图象经过点D,与BC的交点为N. (1)、求反比例函数和一次函数的表达式;(2)、若点P在直线DM上,且使△OPM的面积与四边形OMNC的面积相等,求点P的坐标.22. 如图1, 与 都是等腰直角三角形,直角边 , 在同一条直线上,点 、 分别是斜边 、 的中点,点 为 的中点,连接 , , , , .
(1)、求反比例函数和一次函数的表达式;(2)、若点P在直线DM上,且使△OPM的面积与四边形OMNC的面积相等,求点P的坐标.22. 如图1, 与 都是等腰直角三角形,直角边 , 在同一条直线上,点 、 分别是斜边 、 的中点,点 为 的中点,连接 , , , , . (1)、观察猜想:
(1)、观察猜想:图1中, 与 的数量关系是 , 位置关系是.
(2)、探究证明:将图1中的 绕着点 顺时针旋转 ,得到图2, 与 、 分别交于点 、 ,判断 的形状,并说明理由;
(3)、拓展延伸:把 绕点 任意旋转,若 , ,请直接写出 面积的最大值.
23. 如图,抛物线 经过 , 两点,且与 轴交于点 ,抛物线的对称轴是直线 . (1)、求抛物线的函数表达式;(2)、抛物线与直线 交于 、 两点, 点在 轴上且位于点 的左侧,若以 、 、 为顶点的三角形与 相似,求点 的坐标;(3)、 是直线 上一动点, 为抛物线上一动点,若 为等腰直角三角形,请直接写出点 的坐标.
(1)、求抛物线的函数表达式;(2)、抛物线与直线 交于 、 两点, 点在 轴上且位于点 的左侧,若以 、 、 为顶点的三角形与 相似,求点 的坐标;(3)、 是直线 上一动点, 为抛物线上一动点,若 为等腰直角三角形,请直接写出点 的坐标.