广西玉林市陆川县2016-2017学年七年级下学期数学期末考试试卷
试卷更新日期:2017-09-21 类型:期末考试
一、选择题
-
1. 下列各图中,∠1与∠2是对顶角的是( )A、
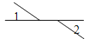 B、
B、 C、
C、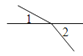 D、
D、 2. 用统计图来描述某班同学的身高情况,最合适的是( )A、条形统计图 B、折线统计图 C、扇形统计图 D、频数分布直方图3.
2. 用统计图来描述某班同学的身高情况,最合适的是( )A、条形统计图 B、折线统计图 C、扇形统计图 D、频数分布直方图3.如图,给出了过直线外一点画已知直线的平行线的方法,其依据是( )
 A、同位角相等,两直线平行 B、内错角相等,两直线平行 C、同旁内角互补,两直线平行 D、两直线平行,同位角相等4. 若m是任意实数,则点M(m2+2,﹣2)在第( )象限.A、一 B、二 C、三 D、四5. 下列调查中,适宜采用全面调查方式的是( )A、调查一架“歼20”战机各零部件的产品质量 B、调查某品牌圆珠笔芯的使用寿命 C、调查市场上酸奶的质量情况 D、调查我市市民对上届巴西奥运会吉祥物的知晓度6.
A、同位角相等,两直线平行 B、内错角相等,两直线平行 C、同旁内角互补,两直线平行 D、两直线平行,同位角相等4. 若m是任意实数,则点M(m2+2,﹣2)在第( )象限.A、一 B、二 C、三 D、四5. 下列调查中,适宜采用全面调查方式的是( )A、调查一架“歼20”战机各零部件的产品质量 B、调查某品牌圆珠笔芯的使用寿命 C、调查市场上酸奶的质量情况 D、调查我市市民对上届巴西奥运会吉祥物的知晓度6.如图,能判定EC∥AB的条件是( )
 A、∠B=∠ACB B、∠B=∠ACE C、∠A=∠ACE D、∠A=∠ECD7. 设a>b>0,c为常数,给出下列不等式①a﹣b>0;②ac>bc;③ < ;④b2>ab,其中正确的不等式有( )A、1个 B、2个 C、3个 D、4个8.
A、∠B=∠ACB B、∠B=∠ACE C、∠A=∠ACE D、∠A=∠ECD7. 设a>b>0,c为常数,给出下列不等式①a﹣b>0;②ac>bc;③ < ;④b2>ab,其中正确的不等式有( )A、1个 B、2个 C、3个 D、4个8.某校260名学生参加植树活动,要求每人值4~7棵,活动结束后调查了每名学生的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.并结合调查数据作出如图所示的扇形统计图,根据统计图提供的信息,可知该校植树量不少于6棵的学生有( )
 A、26名 B、52名 C、78名 D、104名9. 已知二元一次方程组 的解是 ,则(2a﹣1)(b+1)的值为( )A、0 B、2 C、﹣2 D、610. 平面直角坐标系中的点P(2﹣m, m)在第一象限,则m的取值范围在数轴上可表示为( )A、
A、26名 B、52名 C、78名 D、104名9. 已知二元一次方程组 的解是 ,则(2a﹣1)(b+1)的值为( )A、0 B、2 C、﹣2 D、610. 平面直角坐标系中的点P(2﹣m, m)在第一象限,则m的取值范围在数轴上可表示为( )A、 B、
B、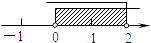 C、
C、 D、
D、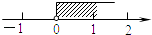 11. 下列命题:①直线a、b、c在同一平面内,如果a⊥b,b∥c,那么a⊥c.②0.01是0.1的算术平方根.③如果a>b,那么ac2>bc2 . ④如果两个角的两边分别平行,那么这两个角相等.⑤如果a<b<0,那么0<ab<a2 . 其中真命题的个数有( )A、1个 B、2个 C、3个 D、4个12. 同学们喜欢足球吗足球一般是用黑白两种颜色的皮块缝制而成,如图所示,黑色皮块是正五边形,白色皮块是正六边形.若一个球上共有黑白皮块32块,请你计算一下,黑色皮块和白色皮块的块数依次为( )
11. 下列命题:①直线a、b、c在同一平面内,如果a⊥b,b∥c,那么a⊥c.②0.01是0.1的算术平方根.③如果a>b,那么ac2>bc2 . ④如果两个角的两边分别平行,那么这两个角相等.⑤如果a<b<0,那么0<ab<a2 . 其中真命题的个数有( )A、1个 B、2个 C、3个 D、4个12. 同学们喜欢足球吗足球一般是用黑白两种颜色的皮块缝制而成,如图所示,黑色皮块是正五边形,白色皮块是正六边形.若一个球上共有黑白皮块32块,请你计算一下,黑色皮块和白色皮块的块数依次为( ) A、16块、16块 B、8块、24块 C、20块、12块 D、12块、20块
A、16块、16块 B、8块、24块 C、20块、12块 D、12块、20块二、填空题
-
13. 把方程3x﹣y=2改写成用含x的代数式表示y的形式,得 .14. 已知 =18.044,那么± = .15. 已知一个样本容量为60,在频数分布直方图中,各小长方形的高比为2:4:1:3,那么第二组的频数是 .16. 不等式组 的整数解为 .17. 小东将书折过来,该角顶点A落在F处,BC为折痕,如图所示,若DB平分∠FBE,∠DBE比∠CBA大30°,设∠CBA和∠DBE分别为x°、y°,那么可求出这两个角的度数的方程组是 .
 18. 某原料供应商对购买其原料的顾客实行如下优惠办法:(1)一次购买金额不超过1万元的不予优惠;(2)一次购买金额超过1万元,但不超过3万元的九折优惠;(3)一次购买金额超过3万元,其中3万元九折优惠,超过3万元的部分八折优惠.某厂因库存原因,第一次在该供应商处购买原料7 800元,第二次购买原料26 100元,如果他是一次性购买同样的原料,可少付款元.
18. 某原料供应商对购买其原料的顾客实行如下优惠办法:(1)一次购买金额不超过1万元的不予优惠;(2)一次购买金额超过1万元,但不超过3万元的九折优惠;(3)一次购买金额超过3万元,其中3万元九折优惠,超过3万元的部分八折优惠.某厂因库存原因,第一次在该供应商处购买原料7 800元,第二次购买原料26 100元,如果他是一次性购买同样的原料,可少付款元.三、解答题
-
19. 综合题(1)、计算 ( ﹣ )﹣| ﹣ |(2)、解方程组(3)、解不等式1﹣ >(4)、解不等式组 ,并把它的解集表示在数轴上.20. 赵军说不等式2a>3a永远不会成立,因为如果在这个不等式两边同除以a,就会出现2>3这样的错误结论.你同意他的说法对吗?若同意说明其依据,若不同意说出错误的原因.21.
如图,AB∥CD,E为AB上一点,∠BED=2∠BAD.
 (1)、求证:AD平分∠CDE;(2)、若AC⊥AD,∠ACD+∠AED=165°,求∠ACD的度数.22. 某课题组为了解全市九年级学生对数学知识的掌握情况,在一次数学检测中,从全市20000名九年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如下图表:
(1)、求证:AD平分∠CDE;(2)、若AC⊥AD,∠ACD+∠AED=165°,求∠ACD的度数.22. 某课题组为了解全市九年级学生对数学知识的掌握情况,在一次数学检测中,从全市20000名九年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如下图表:分数段
频数
频率
50≤x<60
20
0.10
60≤x<70
28
b
70≤x<80
54
0.27
80≤x<90
a
0.20
90≤x<100
24
0.12
100≤x<110
18
0.09
110≤x<120
16
0.08
 (1)、表中a和b所表示的数分别为:a , b;(2)、请在图中补全频数分布直方图;(3)、如果把成绩在70分以上定为合格,那么该市20000名九年级考生数学成绩为合格的学生约有多少名?23. 已知方程组 的解为负整数,求整数a的值.24.
(1)、表中a和b所表示的数分别为:a , b;(2)、请在图中补全频数分布直方图;(3)、如果把成绩在70分以上定为合格,那么该市20000名九年级考生数学成绩为合格的学生约有多少名?23. 已知方程组 的解为负整数,求整数a的值.24.如图,点A,B的坐标分别为(1,0),(0,2),若将线段AB平移到A1B1的坐标分别为(2,a),(b,3),试求a2﹣2b的值.
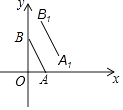 25. 某电器超市销售每台进价分别为200元,170元的A、B联众型号的电风扇,表中是近两周的销售情况:
25. 某电器超市销售每台进价分别为200元,170元的A、B联众型号的电风扇,表中是近两周的销售情况:销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
5台
1800元
第二周
4台
10台
3100元
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)、求A,B两种型号的电风扇的销售单价;(2)、若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?(3)、在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.26. 如图1,点A的坐标为(0,3),将点A向右平移6个单位得到点B,过点B作BC⊥x轴于C. (1)、求B、C两点坐标及四边形AOCB的面积;(2)、点Q自O点以1个单位/秒的速度在y轴上向上运动,点P自C点以2个单位/秒的速度在x轴上向左运动,设运动时间为t秒(0<t<3),是否存在一段时间,使得S△BOQ< ,若存在,求出t的取值范围;若不存在,说明理由.
(1)、求B、C两点坐标及四边形AOCB的面积;(2)、点Q自O点以1个单位/秒的速度在y轴上向上运动,点P自C点以2个单位/秒的速度在x轴上向左运动,设运动时间为t秒(0<t<3),是否存在一段时间,使得S△BOQ< ,若存在,求出t的取值范围;若不存在,说明理由. (3)、求证:S四边形BPOQ是一个定值.
(3)、求证:S四边形BPOQ是一个定值.