广西南宁市马山县2016-2017学年七年级下学期数学期末考试试卷

试卷更新日期：2017-09-21 类型：期末考试

进入出卷网下载

一、选择题

1. 在下列实数： $\frac{π}{2}$ 、 $\sqrt{3}$ 、 $\sqrt[3]{27}$ 、 $\sqrt{16}$ 、 $\frac{22}{7}$ 、﹣0.0010001中，有理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 方程kx+3y=5有一组解是 ${\begin{matrix} x = 2 \\ y = 1 \end{matrix}$ ，则k的值是（）

A、1 B、﹣1 C、0 D、2

查看试题解析
3. 在下列四个汽车标志图案中，能用平移变换来分析其形成过程的图案是（）

A、 B、 C、 D、

查看试题解析
4.
一个不等式组中的两个不等式的解集如图所示，则这个不等式组的解集为（）

A、x＞﹣1 B、x＜1 C、﹣1≤x＜1 D、﹣1＜x≤1

查看试题解析
5.
如图，点E在BC的延长线上，则下列条件中，能判定AD∥BC的是（）

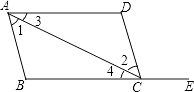A、∠B=∠DCE B、∠3=∠4 C、∠1=∠2 D、∠D+∠DAB=180°

查看试题解析
6. 下列调查：①了解中央电视台“成语大赛”节目的收视率；②调查某城市居民家庭收入情况；③中国首个载货火箭“天舟一号”发射前对重要零部件的检查；④调查某种药品的药效．其中适合抽样调查的是（）

A、①②③ B、①②④ C、②③④ D、①③④

查看试题解析
7. 若P在第二象限，且到x轴的距离为3，到y轴的距离为4，则点P的坐标为（）

A、（3，4） B、（﹣3，4） C、（﹣4，3） D、（4，3）

查看试题解析
8. 若关于x，y的二元一次方程组 ${\begin{matrix} x + y = 5 k \\ x - y = 9 k \end{matrix}$ 的解也是2x+3y＜16的解，则（）

A、k＜0 B、k＜﹣1 C、k＜2 D、k＜1

查看试题解析
9. 父子二人并排竖直站立于游泳池中时，爸爸露出水面的高度是他自身身高的 $\frac{1}{3}$ ，儿子露出水面的高度是他自身身高的 $\frac{1}{4}$ ，父子二人的身高之和为3.4米．若设爸爸的身高为x米，儿子的身高为y米，则可列方程组（）

A、 ${\begin{matrix} x + y = 3.4 \\ \frac{1}{3} x = \frac{1}{4} y \end{matrix}$ B、 ${\begin{matrix} x + y = 3.4 \\ (1 - \frac{1}{3}) x = \frac{1}{4} y \end{matrix}$ C、 ${\begin{matrix} x + y = 3.4 \\ \frac{1}{3} x = (1 - \frac{1}{4}) y \end{matrix}$ D、 ${\begin{matrix} x + y = 3.4 \\ (1 - \frac{1}{3}) x = (1 - \frac{1}{4}) y \end{matrix}$

查看试题解析
10. 把一些图书分给几名同学，如果每人分3本，那么余8本；如果前面的每名同学分5本，那么最后一人就分不到3本．这些图书有（）

A、23本 B、24本 C、25本 D、26本

查看试题解析

二、填空题

11. 实数 $- \sqrt{5}$ 的相反数是．

查看试题解析
12. 如果点P（a，2）和点Q（﹣3，b）关于x轴对称，则点A（a，b）在第象限．

查看试题解析
13. 已知（a﹣2）x^|^a^|^﹣¹+3y=1是关于x、y的二元一次方程，则a= ．

查看试题解析
14. 已知方程组 $\{\begin{matrix} 2 x + y = 4 \\ x + 2 y = 5 \end{matrix}$ ，则x+y的值为．

查看试题解析
15. 不等式：2x﹣1≥3x+1的最大整数解是．

查看试题解析
16.
如图，动点P在平面直角坐标系中按图中箭头所示的方向运动，第1次从原点运动到（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），…，按这样的运动规律，经过2017次运动后，动点P的坐标为

查看试题解析

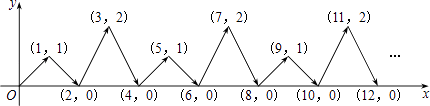
三、解答题

17. 计算：﹣3²+| $\sqrt{2}$ ﹣3|﹣ $\sqrt{{(- 2)}^{2}}$ ．

查看试题解析
18. 解方程组 ${\begin{matrix} 3 x + y = 13 \\ 5 x - y = 3 \end{matrix}$ ．

查看试题解析
19. 解不等式组 ${\begin{matrix} x - 3 (x - 2) \geq 4 \\ \frac{2 x - 1}{5} < \frac{x + 1}{2} \end{matrix}$ ，并将它的解集在数轴上表示出来．

查看试题解析
20.
已知：CD∥AB，OE平分∠AOD，OF⊥OE，∠D=50°，求∠BOF的度数．

查看试题解析
21.
已知△A′B′C′是由△ABC经过平移得到的，它们各顶点在平面直角坐标系中的坐标如下表所示：
△ABC
A（a，0）
B（3，0）
C（5，5）
△A′B′C′
A′（4，2）
B′（7，b）
C′（c，7）

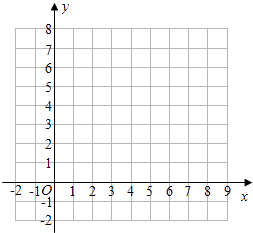(1)、观察表中各对应点坐标的变化，并填空：a= ， b= ， c=；

(2)、在平面直角坐标系中画出△ABC及平移后的△A′B′C′；

(3)、直接写出△A′B′C′的面积是．

查看试题解析
22.
某地区为提倡节约用水，准备实行自来水“阶梯计费”方式，用户用水不超出基本用水量的部分享受基本价格，超出基本用水量的部分实行加价收费．为更好地决策，自来水公司随机抽取部分用户的用水量数据，并绘制了如下不完整的统计图（每组数据包括右端点但不包括左端点），请你根据统计图解答下列问题：

(1)、此次调查抽取了多少用户的用水量数据？

(2)、补全频数分布直方图，求扇形图中“15吨～20吨”部分的圆心角的度数；

(3)、如果自来水公司将基本用水量定为每户25吨，那么该地区40万用户中约有多少用户的用水全部享受基本价格？

查看试题解析
23. 把文字翻译成数学符号，构建方程组模型是解此类题的关键；方案型问题就是要构建双边不等式，有几个整数解就有几种方案.某汽车专卖店销售A，B两种型号的新能源汽车．上周售出1辆A型车和3辆B型车，销售额为96万元；本周已售出2辆A型车和1辆B型车，销售额为62万元．

(1)、求每辆A型车和B型车的售价各为多少元．

(2)、甲公司拟向该店购买A，B两种型号的新能源汽车共6辆，购车费不少于130万元，且不超过140万元．则有哪几种购车方案？

查看试题解析
24.
已知点O（0，0），B（1，2）．

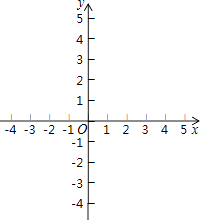(1)、若点A在y轴的正半轴上，且三角形OAB的面积为2，求点A的坐标．

(2)、若点A（3，0），BC∥OA，BC=OA，求点C的坐标．

(3)、若点A（3，0），点D（3，﹣4），求四边形ODAB的面积．

查看试题解析

△ABC	A（a，0）	B（3，0）	C（5，5）
△A′B′C′	A′（4，2）	B′（7，b）	C′（c，7）