浙教版数学八年级上册第一章 三角形的初步知识 单元测试卷
试卷更新日期：2017-09-21 类型：单元试卷
一、单选题
-
1. 如果一个三角形的两边长分别为2和4，则第三边长可能是（ ）A、2 B、4 C、6 D、82. 在一次1500米比赛中，有如下的判断：甲说：丙第一，我第三；乙说：我第一，丁第四；丙说：丁第二，
我第三．结果是每人的两句话中都只说对了一句，则可判断第一名是（ ）
A、甲 B、乙 C、丙 D、丁3. 下列命题中，为真命题的是（ ）A、如果-2x＞-2，那么x＞1 B、如果a2=b2 ， 那么a3=b3 C、面积相等的三角形全等 D、如果a∥b，b∥c，那么a∥c4. 一个三角形的两个内角分别为60°和20°，则这个三角形是（ ）A、直角三角形 B、锐角三角形 C、钝角三角形 D、不能确定5. 如图所示，CE平分∠ACD，∠B=45°，∠ACE=50°，则∠A等于（ ）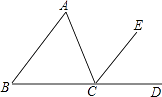
A、45° B、50° C、55° D、95°6. 如图，过△ABC的顶点A，作BC边上的高，以下作法正确的是（ ）A、
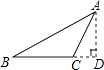B、
C、
D、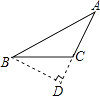
7. 已知△ABC≌△DEF，∠A=70°，∠E=30°，则∠F的度数为（ ）A、80° B、70° C、30° D、100°8. 如图，△ABD≌△ACE，AB=9，AD=7，BD=8，则BE的长是（ ）
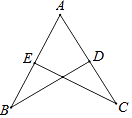A、1 B、2 C、4 D、69. 下列语句正确的是（ ）A、三角形的三条高都在三角形内部 B、三角形的三条中线交于一点 C、三角形不一定具有稳定性 D、三角形的角平分线可能在三角形的内部或外部10. 如图，在△ABC和△DEF中，AB=DE，AB∥DE，添加下列条件仍无法证明△ABC≌△DEF的是（ ）
A、AC∥DF B、∠A=∠D C、AC=DF D、BE=CF二、填空题
-
11. 命题：“如果m是整数，那么它是有理数”，则它的逆命题为： ．12. A、B、C、D、E、F六足球队进行单循环比赛，当比赛到某一天时，统计出A、B、C、D、E、五队已分别比赛了5、4、3、2、1场球，则还没与B队比赛的球队是13. 已知：如图，△ABC≌△ADE，∠BAE=110°，∠BAD=40°，则∠BAC=°．
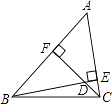
14.如图，已知BE和CF是△ABC的两条高，∠ABC=48°，∠ACB=76°，则∠FDE= ．
15. 长度为2cm、3cm、6cm、7cm、8cm的五条线段，若以其中的三条线段为边构成三角形，可以构成不同的三角形共有个．三、解答题
-
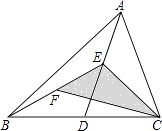
16. 如图，在△ABC中，已知点D、E、F分别为BC、AD、BE的中点，且S△ABC=8cm2 ， 则图中阴影部分△CEF的面积是多少？
17. 如图，△ABC≌△ADE，且∠CAD=10°，∠B=∠D=25°，∠EAB=120°，求∠DFB和∠DGB的度数．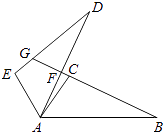
18. 如图，已知△ABF≌△DEC，说明AC∥DF成立的理由．
19. 如图，OC平分∠AOB，点D，E分别在OA，OB上，点P在OC上且有PD=PE．求证：∠PDO+∠PEO=180°．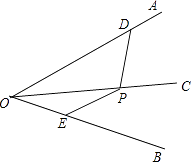
四、综合题
-
20.
如图，点D，E在△ABC的边BC上，连接AD，AE．下面有三个等式：①AB=AC；②AD=AE；③BD=CE．以此三个等式中的两个作为命题的题设，另一个作为命题的结论，相构成以下三个命题：命题Ⅰ“如果①②成立，那么③成立”； 命题Ⅱ“如果①③成立，那么②成立”；命题Ⅲ“如果②③成立，那么①成立”．
(1)、以上三个命题是真命题的为（直接作答）；(2)、请选择一个真命题进行证明（先写出所选命题，然后证明）．21.如图1，△ABE是等腰三角形，AB=AE，∠BAE=45°，过点B作BC⊥AE于点C，在BC上截取CD=CE，连接AD、DE并延长AD交BE于点P；
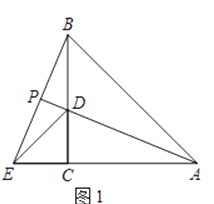(1)、求证：AD=BE；(2)、试说明AD平分∠BAE；(3)、如图2，将△CDE绕着点C旋转一定的角度，那么AD与BE的位置关系是否发生变化，说明理由．
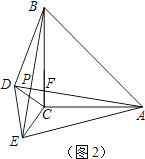22. 等腰三角形的判定定理：已知△ABC中，∠B=∠C，求证：AB=AC课堂情景还原：
小明说：“作高线AD，可证明△ABD≌△ACD，从而得到AB=AC”
小红说：“作角平分线AD，可证明△ABD≌△ACD，从而得到AB=AC”
小刚说：“作中线AD，证明△ABD≌△ACD”
很多同学说不能证明△ABD≌△ACD，因为“SSA”不能作为判定两个三角形全等的依据．
小聪是这样分析的：“中线AD把△ABC面积平分，即△ABD与△ACD面积相等，要证明AB=AC，只需证明这两边上的高相等…”
(1)、小明与小红证明全等的判定方法是：（简写理由）(2)、根据小聪的提示，请你完成等腰三角形的判定定理证明．
