广西柳州市2016-2017学年七年级下学期数学期末考试试卷

试卷更新日期：2017-09-21 类型：期末考试

进入出卷网下载

一、选择题

1. 在﹣1， $\frac{1}{3}$ ， $\sqrt{2}$ ，0.7中，无理数是（）

A、﹣1 B、 $\frac{1}{3}$ C、 $\sqrt{2}$ D、0.7

查看试题解析
2. 8的立方根为（）

A、±2 B、2 C、4 D、±4

查看试题解析
3. 如图，与∠1是同位角的是（）

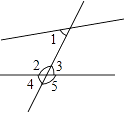A、∠2 B、∠3 C、∠4 D、∠5

查看试题解析
4. 若m＞n，下列不等式一定成立的是（）

A、m﹣2＞n+2 B、2m＞2n C、﹣ $\frac{m}{2}$ ＞ $\frac{n}{2}$ D、m²＞n²

查看试题解析
5. 下列命题是真命题的是（）

A、同位角相等 B、有且只有一条直线与已知直线垂直 C、垂线段最短 D、直线外一点到这条直线的垂线段，叫做点到直线的距离

查看试题解析
6. 下面调查中，适合采用全面调查的事件是（）

A、对全国中学生心理健康现状的调查 B、谋批次汽车的抗重击能力的调查 C、春节联欢会晚会收视率的调查 D、对你所在的班级同学的身高情况的调查

查看试题解析
7. 估算 $\sqrt{65}$ 的值介于（）

A、5到6之间 B、6到7之间 C、7到8之间 D、8到9之间

查看试题解析
8.
如图，直线AB与直线CD相交于点O，MO⊥AB，垂足为O，已知∠AOD=136°，则∠COM的度数为（）

A、36° B、44° C、46° D、54°

查看试题解析
9. 若方程组 ${\begin{matrix} a x + y = 5 \\ x + b y = - 1 \end{matrix}$ 的解为 ${\begin{matrix} x = 2 \\ y = 1 \end{matrix}$ ，则点P（a，b）所在的象限为（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
10. 平面直角坐标系中，点A（﹣3，2），B（3，4），C（x，y），若AC∥x轴，则线段BC的最小值及此时点C的坐标分别为（　　）

A、6，（﹣3，4） B、2，（3，2） C、2，（3，0） D、1，（4，2）

查看试题解析

二、填空题

11. 如果用（7，1）表示七年级一班，那么八年级五班可表示成．

查看试题解析
12. 计算： $3 \sqrt{5} - 2 \sqrt{5}$ = ．

查看试题解析
13. 某市有6500名九年级学生参加数学毕业考试，为了了解这些学生毕业考试的数学成绩，从6500份数学答卷中随机抽取了300份进行统计分析，在这个问题中，样本容量是．

查看试题解析
14. 已知方程2x+y﹣5=0，用含x的代数式表示y= ．

查看试题解析
15. 若不等式组 ${\begin{matrix} x < 8 \\ x > m \end{matrix}$ 无解，则m的取值范围是．

查看试题解析
16.
如图，已知A₁（1，0），A₂（1，1），A₃（﹣1，1），A₄（﹣1，﹣1），A₅（2，﹣1），…则点A₂₀₁₇的坐标为．

查看试题解析

三、解答题

17. 解方程组： ${\begin{matrix} 2 x - y = 5 \\ x + y = 4 \end{matrix}$ ．

查看试题解析
18.
解不等式组 ${\begin{matrix} x + 3 > 1 \\ 2 x - 1 < 5 \end{matrix}$ ，并把解集在数轴上表示出来．

查看试题解析
19.
已知，点A（4，3），B（3，1），C（1，2）．

(1)、在平面直角坐标系中分别描出A，B，C三点，并顺次连接成△ABC；

(2)、将△ABC向左平移6个单位，再向下平移5个单位得到△A₁B₁C₁；画出△A₁B₁C₁ ，并写出点A₁ ， B₁ ， C₁的坐标．

查看试题解析
20.
某学校为了了解八年级500名男生体能的情况，从中随机抽取了部分男生进行1分钟跳绳次数测试，将数据整理后，绘制成如下不完整的频数分布表和频数分布直方图：
分组
频数
频率
90≤x＜100
2
0.04
100≤x＜110
6
0.12
110≤x＜120
8
b
120≤x＜130
14
0.28
130≤x＜140
a
0.32
140≤x＜150
4
0.08
请根据图表信息回答下列问题：

(1)、这次参加测试的男生共人，表中a= ， b= ．

(2)、请补全频数分布直方图；

(3)、如果1分钟跳绳次数x在120（含120次）以上的为“合格”，请估计该校八年级男生跳绳次数为“合格”的人数．

查看试题解析
21.
如图，已知AB∥CD，BC∥ED，请你猜想∠B与∠D之间具有什么数量关系，并说明理由．

查看试题解析
22. 小李新家装修，在装修客厅时，购进彩色地砖和单色地砖共80块，共花费4000元．已知彩色地砖的单价是80元/块，单色地砖的单价是40元/块．

(1)、两种型号的地砖各采购了多少块？

(2)、如果厨房也铺设这两种型号的地砖共30块，且采购地砖的费用不超过1600元，那么彩色地砖最多能采购多少块？

查看试题解析
23.
如图1，在平面直角坐标系中，OA=7，OC=18，将点C先向上平移7个单位，再向左平移4个单位，得到点B，连接AB，BC．

(1)、填空：点B的坐标为；

(2)、
如图2，BF平分∠ABC交x轴于点F，CD平分∠BCO交BF于点D，过点F作FH⊥BF交BC的延长线于点H，试判断DC与FH的位置关系，并说明理由；

(3)、若点P从点C出发以每秒2个单位长度的速度沿CO方向移动，同时点Q从点O出发以每秒1个单位长度的速度沿OA方向移动，设移动的时间为t秒（0＜t＜7），四边形OPBA与△OQB的面积分别记为S1，S2，是否存在一段时间，使S₁＜2S₂？若存在，求出t的取值范围；若不存在，试说明理由．

查看试题解析

分组	频数	频率
90≤x＜100	2	0.04
100≤x＜110	6	0.12
110≤x＜120	8	b
120≤x＜130	14	0.28
130≤x＜140	a	0.32
140≤x＜150	4	0.08