河北省张家口市涿鹿县2019-2020学年七年级下学期数学期中考试试卷
试卷更新日期:2020-06-22 类型:期中考试
一、单选题
-
1. 的平方根是( )A、 B、 C、 D、2. 下列各点属于第三象限的点是 ( )A、(2,3) B、(2,-3) C、(-2,-3) D、(-2,3)3. 如图,下列能判定AB∥CD的条件的个数是( )
①∠B+∠BCD=180°;②∠2=∠3;③∠1=∠4;④∠B=∠5.
 A、1个 B、2个 C、3个 D、4个4. 下列命题中,是假命题的是( )A、两点之间,线段最短 B、同旁内角互补 C、直角的补角仍然是直角 D、对顶角相等5. 在 、1.414、 、π、 中,无理数的个数有( )A、1个 B、2个 C、3个 D、4个6. 下列说法正确的是( ).A、若 ,则x=2 B、9的平方根是3 C、-27的立方根是-9 D、7. 如图,能表示点到直线的距离的线段共有( )
A、1个 B、2个 C、3个 D、4个4. 下列命题中,是假命题的是( )A、两点之间,线段最短 B、同旁内角互补 C、直角的补角仍然是直角 D、对顶角相等5. 在 、1.414、 、π、 中,无理数的个数有( )A、1个 B、2个 C、3个 D、4个6. 下列说法正确的是( ).A、若 ,则x=2 B、9的平方根是3 C、-27的立方根是-9 D、7. 如图,能表示点到直线的距离的线段共有( )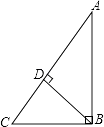 A、2条 B、3条 C、4条 D、5条8. 下列图形中,哪个可以通过图1平移得到( )。
A、2条 B、3条 C、4条 D、5条8. 下列图形中,哪个可以通过图1平移得到( )。 A、
A、 B、
B、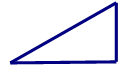 C、
C、 D、
D、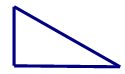 9. 点A(-3,5)关于x轴对称的点的坐标是( )A、(-3,-5) B、(3,-5) C、(3,5) D、(-3,5)10. 实数a、b在数轴上对应点的位置如图所示,则化简 ﹣|a+b|的结果为( )
9. 点A(-3,5)关于x轴对称的点的坐标是( )A、(-3,-5) B、(3,-5) C、(3,5) D、(-3,5)10. 实数a、b在数轴上对应点的位置如图所示,则化简 ﹣|a+b|的结果为( ) A、﹣2a+b B、b C、2a+b D、﹣2a﹣b11. 点P在第三象限,点P到 轴的距离是5,到 轴的距离是3,则点P的坐标( )A、(3,-5) B、(-5,-3) C、(-3,-5) D、(-3,5)12. 已知在同一平面内三条直线a、b、c,若a∥c,b∥c,则a与b的位置关系是( )A、a⊥b B、a⊥b或a∥b C、a∥b D、无法确定13. 在如图所示的四种沿AB进行折叠的方法中,不一定能判断纸带两条边a,b互相平行的是( )
A、﹣2a+b B、b C、2a+b D、﹣2a﹣b11. 点P在第三象限,点P到 轴的距离是5,到 轴的距离是3,则点P的坐标( )A、(3,-5) B、(-5,-3) C、(-3,-5) D、(-3,5)12. 已知在同一平面内三条直线a、b、c,若a∥c,b∥c,则a与b的位置关系是( )A、a⊥b B、a⊥b或a∥b C、a∥b D、无法确定13. 在如图所示的四种沿AB进行折叠的方法中,不一定能判断纸带两条边a,b互相平行的是( ) A、如图1,展开后测得∠1=∠2 B、如图2,展开后测得∠1=∠2且∠3=∠4 C、如图3,测得∠1=∠2 D、在图④中,展开后测得∠1+∠2=180°
A、如图1,展开后测得∠1=∠2 B、如图2,展开后测得∠1=∠2且∠3=∠4 C、如图3,测得∠1=∠2 D、在图④中,展开后测得∠1+∠2=180°二、填空题
-
14. 的算术平方根是 , =.
15. 将命题“内错角相等”,写成“如果……,那么……”的形式:.16. 课间操时,小华、小军、小刚的位置如图,小军对小华说,如果我的位置用(0,﹣2)表示,小刚的位置用(2,0)表示,那么你的位置可以表示为 . 17. 如图,已知 , , ,则 .
17. 如图,已知 , , ,则 .
三、解答题
-
18.(1)、计算: .(2)、求式子(x+1)2=9中x的值.19. 如图,已知∠1+∠2﹦180°,∠3﹦∠B , 则DE∥BC , 下面是王华同学的推导过程,请你帮他在括号内填上推导依据或内容.

证明:
∵∠1+∠2﹦180(已知)
∠1﹦∠4 ()
∴∠2﹢﹦180°.
∴EH∥AB()
∴∠B﹦∠EHC()
∵∠3﹦∠B(已知)
∴ ∠3﹦∠EHC()
∴ DE∥BC()
20. 已知2a-1的平方根是±3,3a-b+2的算术平方根是4,求a+3b的立方根.21. 在平面直角坐标中表示下面各点:A(0,3),B(1,﹣3),C(3,﹣5),D(﹣3,﹣5),E(3,5),F(5,7)
(1) A点到原点O的距离是 ;
(2) 将点C向x轴的负方向平移6个单位它与点 重合;
(3) 连接CE,则直线CE与y轴位置关系是 ;
(4) 点F分别到x、y轴的距离分别是 。