山西省太原市2019-2020学年八年级下学期数学期中考试试卷
试卷更新日期:2020-06-22 类型:期中考试
一、单选题
-
1. 下列四个图形中,可以通过基本图形平移得到的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列车标中,既是中心对称图形,又是轴对称图形的是( )A、
2. 下列车标中,既是中心对称图形,又是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 若 ,则下列变形错误的是( )A、 B、 C、 D、4. 在数轴上表示不等式x≥-2的解集正确的是( )A、
3. 若 ,则下列变形错误的是( )A、 B、 C、 D、4. 在数轴上表示不等式x≥-2的解集正确的是( )A、 B、
B、 C、
C、 D、
D、 5. 不等式2x﹣7<5﹣2x的正整数解有( )A、4个 B、3个 C、2个 D、1个6. 实数 在数轴上对应点的位置如图所示,则下列结论正确的是( )
5. 不等式2x﹣7<5﹣2x的正整数解有( )A、4个 B、3个 C、2个 D、1个6. 实数 在数轴上对应点的位置如图所示,则下列结论正确的是( )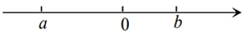 A、 B、 C、 D、7. 如图,一次函数 的图象经过点 ,则关于 的不等式 的解集为( )
A、 B、 C、 D、7. 如图,一次函数 的图象经过点 ,则关于 的不等式 的解集为( )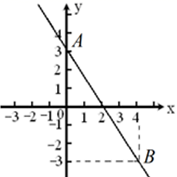 A、 B、 C、 D、8. 判断以下各组线段为边作三角形,可以构成直角三角形的是( )A、6,15,17 B、7,12,15 C、13,15,20 D、7,24,259. 如图,在△ABC中,AB=AC,D为BC中点,∠BAD=35°,则∠C的度数为( )
A、 B、 C、 D、8. 判断以下各组线段为边作三角形,可以构成直角三角形的是( )A、6,15,17 B、7,12,15 C、13,15,20 D、7,24,259. 如图,在△ABC中,AB=AC,D为BC中点,∠BAD=35°,则∠C的度数为( )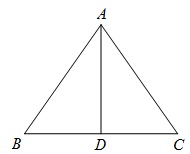 A、35° B、45° C、55° D、60°10. 如图,在 中, ,则 的度数为( )
A、35° B、45° C、55° D、60°10. 如图,在 中, ,则 的度数为( ) A、 B、 C、 D、11. 如图,在 中, 将 绕点 顺时针方向旋转得到 当点 的对应点 恰好落在 边上时,则 的长为( )
A、 B、 C、 D、11. 如图,在 中, 将 绕点 顺时针方向旋转得到 当点 的对应点 恰好落在 边上时,则 的长为( )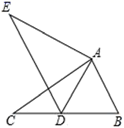 A、 B、 C、 D、12. 如图, 中, 是 的角平分线, 的垂直平分线分别交 于点 ,则下列结论不一定成立的是( )
A、 B、 C、 D、12. 如图, 中, 是 的角平分线, 的垂直平分线分别交 于点 ,则下列结论不一定成立的是( ) A、 B、 C、 D、13. 如图,已知 中, 的垂直平分线分别交 于 连接 ,则 的长为( )
A、 B、 C、 D、13. 如图,已知 中, 的垂直平分线分别交 于 连接 ,则 的长为( ) A、 B、 C、 D、14. 如图,将 绕点 逆时针旋转 得到 点 的对应点分别为 则 的长为( )
A、 B、 C、 D、14. 如图,将 绕点 逆时针旋转 得到 点 的对应点分别为 则 的长为( ) A、 B、 C、 D、15. 如图,在 中, 分别是 上的点,且 ,则 的度数为( )
A、 B、 C、 D、15. 如图,在 中, 分别是 上的点,且 ,则 的度数为( )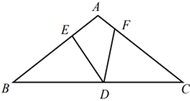 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
16. 用不等式表示关系: 的 倍与 的差不小于零 .17. 如图,把三角板的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,则顶点C平移的距离CC'=.
 18. 如图,小亮为了测量校园里教学楼 的高度,他站在离教学楼 的 处仰望教学楼顶部 仰角为 .已知小亮的高度是 则教学楼的高度约为 结果精确到 .
18. 如图,小亮为了测量校园里教学楼 的高度,他站在离教学楼 的 处仰望教学楼顶部 仰角为 .已知小亮的高度是 则教学楼的高度约为 结果精确到 . 19. 如图,点 分别是等边三角形 的边 的点,且 与 相交于点 .则 的度数为 .
19. 如图,点 分别是等边三角形 的边 的点,且 与 相交于点 .则 的度数为 .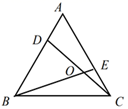 20. 某种品牌自行车的进价为 元,出售时标价为 元,商店准备打折出售,但要保持利润率不低于 ,则至多可打折.
20. 某种品牌自行车的进价为 元,出售时标价为 元,商店准备打折出售,但要保持利润率不低于 ,则至多可打折.
三、解答题
-
21. 解不等式组: ,并把解集在数轴上表示出来.22. “一方有难,八方支援.某学校计划购买 消毒液和 酒精消毒水共 瓶,用于支援武汉抗击“新冠肺炎疫情”.已知 消毒液的单价为 元/瓶, 酒精消毒水的单价为13元/瓶.若购买这批物资的总费用不超过 元,求至少可以购买 消毒液多少瓶?23. 综合与实践
问题情境
数学活动课上,老师让同学们以“三角形平移与旋转”为主题开展数学活动, 和 是两个等边三角形纸片,其中, .
解决问题
(1)、勤奋小组将 和 按图1所示的方式摆放(点 在同一条直线上) ,连接 .发现 ,请你给予证明; (2)、如图2,创新小组在勤奋小组的基础上继续探究,将 绕着点 逆时针方向旋转,当点 恰好落在 边上时,求 的面积;
(2)、如图2,创新小组在勤奋小组的基础上继续探究,将 绕着点 逆时针方向旋转,当点 恰好落在 边上时,求 的面积; (3)、如图3,缜密小组在创新小组的基础上,提出一个问题: “将 沿 方向平移 得到 连接 ,当 恰好是以 为斜边的直角三角形时,求 的值.请你直接写出 的值.
(3)、如图3,缜密小组在创新小组的基础上,提出一个问题: “将 沿 方向平移 得到 连接 ,当 恰好是以 为斜边的直角三角形时,求 的值.请你直接写出 的值. 由题意得∠ACD= =60°,
由题意得∠ACD= =60°,∵∠ =90°,
∴ ,
∵ ,
∴ ,
∴ =2cm,
∴a=2.
