河北省张家口市涿鹿县2019-2020学年八年级下学期数学期中考试试卷

试卷更新日期：2020-06-22 类型：期中考试

进入出卷网下载

一、单选题

1. 若二次根式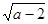有意义，则a的取值范围是（）

A、a≥2 B、a≤2 C、a＞2 D、a≠2

查看试题解析
2. 以下各组数据为三角形的三边长，能构成直角三角形的是（）

A、 $2 \sqrt{2}, 2 \sqrt{2}, 4$ B、2，3，4 C、2，2，1 D、4，5，6

查看试题解析
3. 菱形的两条对角线长分别为6，8，则它的周长是（）

A、5 B、10 C、20 D、24

查看试题解析
4. 下列各式中，最简二次根式是（）

A、 $\sqrt{27}$ B、 $\sqrt{m^{5} n^{2}}$ C、 $\sqrt{\frac{1}{2}}$ D、 $\sqrt{6}$

查看试题解析
5. 如图，在矩形 $A B C D$ 中，对角线 $A C$ 与 $B D$ 相交于点 $O$ ，若 $∠ C O D = 50 °$ ，那么 $∠ C A D$ 的度数是（）

A、 $30 °$ B、 $20 °$ C、 $40 °$ D、 $25 °$

查看试题解析
6. 下列计算正确的是（）

A、 $\frac{\sqrt{8}}{2} = \sqrt{4}$ B、 $\sqrt{{(- 3)}^{2}} = 3$ C、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ D、 $2 + \sqrt{2} = 2 \sqrt{2}$

查看试题解析
7. 如图，三角形是直角三角形，四边形是正方形，已知正方形A的面积是64，正方形B的面积是100，则半圆C的面积是（）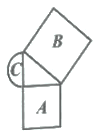

A、36 B、4.5π C、9π D、18π

查看试题解析
8. 如图，在平行四边形ABCD中，BC＝7，CE平分∠BCD交AD边于点E，且AE＝3，则AB的长为（）

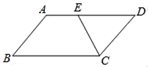A、5 B、4 C、3 D、 $\frac{3}{2}$

查看试题解析
9. 如图，在△ABC中，点D在BC上，DE∥AC，DF∥AB，下列四个判断中错误的是（）

A、四边形AEDF是平行四边形 B、若∠BAC＝90°，则四边形AEDF是矩形 C、若AD平分∠BAC，则四边形AEDF是矩形 D、若AD⊥BC且AB＝AC，则四边形AEDF是菱形

查看试题解析
10. 在将式子 $\frac{m}{\sqrt{m}}$ （m＞0）化简时，
小明的方法是： $\frac{m}{\sqrt{m}}$ = $\frac{m^{} \sqrt{m}}{\sqrt{m} \cdot \sqrt{m}}$ = $\frac{m \sqrt{m}}{m}$ = $\sqrt{m}$ ；

小亮的方法是： $\frac{m}{\sqrt{m}} = \frac{{(\sqrt{m})}^{2}}{\sqrt{m}} = \sqrt{m}$ ；

小丽的方法是： $\frac{m}{\sqrt{m}} = \frac{\sqrt{m^{2}}}{\sqrt{m}} = \sqrt{\frac{m^{2}}{m}} = \sqrt{m}$ .

则下列说法正确的是（　　）

A、小明、小亮的方法符合题意，小丽的方法不符合题意 B、小明、小丽的方法符合题意，小亮的方法不符合题意 C、小明、小亮、小丽的方法都符合题意 D、小明、小丽、小亮的方法都不符合题意

查看试题解析
11. 如图，OP=1，过点P作PP₁⊥OP且PP₁=1，得OP₁= $\sqrt{2}$ ；再过点P₁作P₁P₂⊥OP₁且P₁P₂=1，得OP₂= $\sqrt{3}$ ；又过点P₂作P₂P₃⊥OP₂且P₂P₃=1，得OP₃=2……依此法继续作下去，得OP₂₀₁₇=（）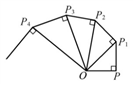

A、 $\sqrt{2015}$ B、 $\sqrt{2016}$ C、 $\sqrt{2017}$ D、 $\sqrt{2018}$

查看试题解析
12. 如图， $▱$ $A B C D$ 的对角线AC，BD相交于点O， $E$ 是AB中点，且AE+EO=4，则 $▱ A B C D$ 的周长为（）

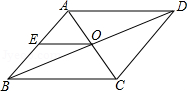A、20 B、16 C、12 D、8

查看试题解析
13. 如图所示，实数a、b在数轴上的位置化简 $\sqrt{a^{2}} - \sqrt{b^{2}} + \sqrt{{(a - b)}^{2}}$ 的结果是（）

A、﹣2a B、﹣2b C、0 D、2a﹣2b

查看试题解析
14. “赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较长直角边长为a，较短直角边长为b，若（a+b）²=21，大正方形的面积为13，则小正方形的面积为（）

A、3 B、4 C、5 D、6

查看试题解析

二、填空题

15. 比较大小： $2 \sqrt{3}$ $3 \sqrt{2}$ ．（填“＞、＜、或=”）

查看试题解析
16. 写出“平行四边形的两组对边分别相等”的逆命题，并判断真假：．

查看试题解析
17. 在四边形ABCD中，对角线AC ， BD交于点O且AC ， BD互相平分，若添加一个条件使得四边形ABCD是矩形，则这个条件可以是(填写一个即可)．

查看试题解析
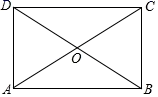18. 如图，正方形ABCD的边长为3，点E在边AB上，且BE＝1，若点P在对角线BD上移动，则PA+PE的最小值是．

查看试题解析
19.

(1)、计算填空： $\sqrt{4^{2}}$ ＝， $\sqrt{{0.8}^{2}}$ ＝， $\sqrt{{(- 3)}^{2}}$ ＝， $\sqrt{{(- \frac{2}{3})}^{2}}$ ＝

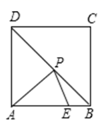(2)、根据计算结果，回答： $\sqrt{a^{2}}$ 一定等于a吗？你发现其中的规律了吗？并请你把得到的规律描述出来？

(3)、利用你总结的规律，计算： $\sqrt{{(π - 3.15)}^{2}}$

查看试题解析

三、解答题

20. 化简：

(1)、 $\sqrt{\frac{12}{25}}$

(2)、 $\frac{\sqrt{15} \times \sqrt{3}}{\sqrt{5}}$

(3)、 $\sqrt{12} - \sqrt{3} + \sqrt{\frac{1}{3}}$

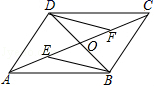
(4)、 $(\sqrt{5} + \sqrt{2}) (\sqrt{5} - \sqrt{2})$

查看试题解析
21. 如图，▱ABCD的对角线AC，BD相交于点O，点E、F在AC上，且AF=CE．
求证：BE=DF．

查看试题解析
22. 在Rt△ABC中，∠BAC=90°，D是BC的中点，E是AD的中点．过点A作AF∥BC交BE的延长线于点F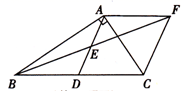

(1)、求证：△AEF≌△DEB；

(2)、证明四边形ADCF是菱形；

(3)、若AC=4，AB=5，求菱形ADCFD 的面积．

查看试题解析
23. 如图，某住宅小区在施工过程中留下了一块空地（图中的四边形ABCD），经测量，在四边形ABCD中，AB＝3m，BC＝4m，CD＝12m，DA＝13m，∠B＝90°．

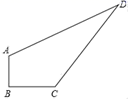(1)、△ACD是直角三角形吗？为什么？

(2)、小区为美化环境，欲在空地上铺草坪，已知草坪每平方米80元，试问铺满这块空地共需花费多少元？

查看试题解析
24. 阅读下面材料：
在数学课上，老师请同学思考如下问题：如图1，我们把一个四边形ABCD的四边中点E，F，G，H依次连接起来得到的四边形EFGH是平行四边形吗.

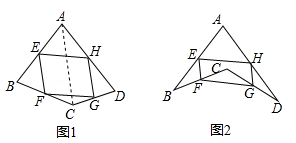
小敏在思考问题时，有如下思路：连接AC.

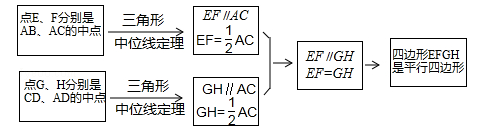
结合小敏的思路作答：

(1)、若只改变图1中四边形ABCD的形状（如图2），则四边形EFGH还是平行四边形吗？说明理由，参考小敏思考问题的方法解决一下问题；

(2)、如图2，在（1）的条件下，若连接AC，BD.
①当AC与BD满足什么条件时，四边形EFGH是菱形，写出结论并证明；

②当AC与BD满足什么条件时，四边形EFGH是矩形，直接写出结论.

查看试题解析