北京市房山区2019-2020学年八年级下学期数学期中考试试卷
试卷更新日期:2020-06-22 类型:期中考试
一、单选题
-
1. 在平面直角坐标系中,点P(-2,5)位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列各曲线中,不表示y是 x的函数的是( )A、
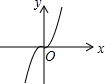 B、
B、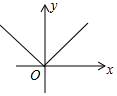 C、
C、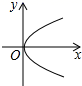 D、
D、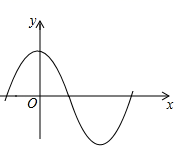 3. 若点 A(2,y1),B(3,y2)都在一次函数图象 上,则y1与 y2的大小关系是( )A、y1>y2 B、y1=y2 C、y1<y2 D、无法比较大小4. 下列实数中,方程x2-2x=0 的根是( )A、0 B、2 C、0或1 D、0或25. 一元二次方程2x2+6x+3= 0 经过配方后可变形为( )A、 =6 B、 =12 C、 D、6. 对于一次函数 y =kx + b (k, b 为常数),下表中给出几组自变量及其对应的函数值,
3. 若点 A(2,y1),B(3,y2)都在一次函数图象 上,则y1与 y2的大小关系是( )A、y1>y2 B、y1=y2 C、y1<y2 D、无法比较大小4. 下列实数中,方程x2-2x=0 的根是( )A、0 B、2 C、0或1 D、0或25. 一元二次方程2x2+6x+3= 0 经过配方后可变形为( )A、 =6 B、 =12 C、 D、6. 对于一次函数 y =kx + b (k, b 为常数),下表中给出几组自变量及其对应的函数值,x
-1
0
1
3
y
7
5
2
-1
其中恰好有一个函数值计算有误,则这个错误的函数值是( )
A、-1 B、2 C、5 D、77. 如图,若点P为函数 图象上的一动点, 表示点P到原点O的距离,则下列图象中,能表示 与点P的横坐标 的函数关系的图象大致是( )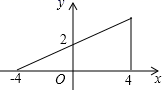 A、
A、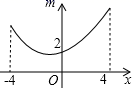 B、
B、 C、
C、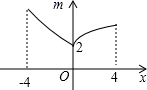 D、
D、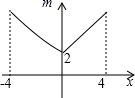 8. 为了让市民享受到更多的优惠,相关部门拟确定一个折扣线,计划使50%左右的人获得折扣优惠.某市针对乘坐地铁的人群进行了调查.调查小组在各地铁站随机调查了该市1000人上一年乘坐地铁的月均花费(单位:元),绘制了频数分布直方图,如图所示.下列说法正确的是( )
8. 为了让市民享受到更多的优惠,相关部门拟确定一个折扣线,计划使50%左右的人获得折扣优惠.某市针对乘坐地铁的人群进行了调查.调查小组在各地铁站随机调查了该市1000人上一年乘坐地铁的月均花费(单位:元),绘制了频数分布直方图,如图所示.下列说法正确的是( )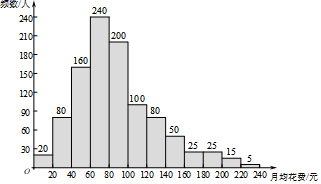
①每人乘坐地铁的月均花费最集中的区域在80~100元范围内;
②每人乘坐地铁的月均花费的平均数范围是40~60元范围内;
③每人乘坐地铁的月均花费的中位数在60~100元范围内;
④乘坐地铁的月均花费达到80元以上的人可以享受折扣.
A、①②④ B、①③④ C、③④ D、①②二、填空题
-
9. 若点P(-1,a)与Q(b,2)关于x轴对称,则a+b= .10. 2022年将在北京—张家口举办冬季奥运会,北京将成为世界上第一个既举办夏季奥运会,又举办冬季奥运会的城市.某队要从两名选手中选取一名参加比赛,为此对这两名队员进行了五次测试,测试成绩如图所示,你会选择选手(填A或B),理由是 .
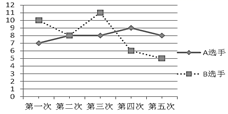 11. 若一次函数 ( )的图象如图所示,点P(2.5,3)在函数图象上,则关于x的方程 的解是 .
11. 若一次函数 ( )的图象如图所示,点P(2.5,3)在函数图象上,则关于x的方程 的解是 .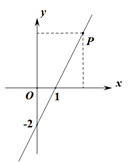 12. 关于x的一元二次方程ax2+bx-2020=0有一个根为x=-1,写出一组满足条件的实数a,b的值:a= , b= .13. 一个y关于x的函数同时满足以下两个条件:(1)图象经过点(-3,4);(2)y随x增大而减小这个函数的表达式可以是 . (写出一个即可)14. 若关于x的一元二次方程 有两个不相等的实数根,则m的取值范围是 .15. 如图,在平面直角坐标系xOy中,一次函数y=x+1与x、y 轴分别交于点A、B,在直线 AB上截取BB1=AB,过点B1分别作y 轴的垂线,垂足为点C1 , 得到⊿BB1C1;在直线 AB上截取B1B2= BB1 , 过点B2分别作y 轴的垂线,垂足为点C2 , 得到⊿BB2C2;在直线AB上截取B2B3= B1B2 , 过点B3作y 轴的垂线,垂足为点C3 , 得到⊿BB3C3;……;第3个⊿BB3C3的面积是;第n个⊿BBnCn的面积是(用含n的式子表示,n是正整数).
12. 关于x的一元二次方程ax2+bx-2020=0有一个根为x=-1,写出一组满足条件的实数a,b的值:a= , b= .13. 一个y关于x的函数同时满足以下两个条件:(1)图象经过点(-3,4);(2)y随x增大而减小这个函数的表达式可以是 . (写出一个即可)14. 若关于x的一元二次方程 有两个不相等的实数根,则m的取值范围是 .15. 如图,在平面直角坐标系xOy中,一次函数y=x+1与x、y 轴分别交于点A、B,在直线 AB上截取BB1=AB,过点B1分别作y 轴的垂线,垂足为点C1 , 得到⊿BB1C1;在直线 AB上截取B1B2= BB1 , 过点B2分别作y 轴的垂线,垂足为点C2 , 得到⊿BB2C2;在直线AB上截取B2B3= B1B2 , 过点B3作y 轴的垂线,垂足为点C3 , 得到⊿BB3C3;……;第3个⊿BB3C3的面积是;第n个⊿BBnCn的面积是(用含n的式子表示,n是正整数).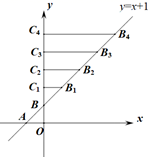
三、解答题
-
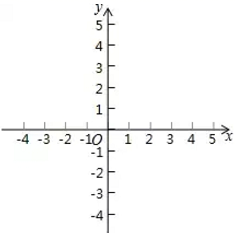
16. 用公式法解方程: .17. 解方程: .18. 函数 是关于x的一次函数,且y随着x的增大而减小,求m的取值范围并指出图象经过哪几个象限?19. 已知关于x的一元二次方程mx2-(m+2)x+2=0(m≠0)(1)、求证:方程一定有两个实数根;(2)、若此方程的两根为不相等的整数,求整数m的值.20. 已知一次函数(1)、在平面直角坐标系内画出该函数的图象;(2)、当自变量x=-4时,函数y的值;(3)、当x<0时,请结合图象,直接写出y的取值范围: .
 21. 在平面直角坐标系xOy中,已知点 、点 ,一次函数 的图象与直线AB交于点P.(1)、求直线AB的函数表达式及P点的坐标;(2)、若点Q是y轴上一点,且△BPQ的面积为2,求点Q的坐标.22. 列方程解应用题:北京大兴国际机场,是建设在北京市大兴区与河北省廊坊市广阳区之间的超大型国际航空综合交通枢纽.机场主体工程占地多在北京境内,70万平米航站楼,客机近机位92个。2019年9月25日,北京大兴国际机场正式投入运营. 据调查,10月大兴机场载客量约为112万人,12月载客量约为175万人,若10月到12月载客量的月增长率相同,求每月载客量的平均月增长率?23. 第二十四届冬季奥林匹克运动会将于2022年在北京市和张家口市举行.为了调查学生对冬奥知识的了解情况,从甲、乙两校各随机抽取20名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
21. 在平面直角坐标系xOy中,已知点 、点 ,一次函数 的图象与直线AB交于点P.(1)、求直线AB的函数表达式及P点的坐标;(2)、若点Q是y轴上一点,且△BPQ的面积为2,求点Q的坐标.22. 列方程解应用题:北京大兴国际机场,是建设在北京市大兴区与河北省廊坊市广阳区之间的超大型国际航空综合交通枢纽.机场主体工程占地多在北京境内,70万平米航站楼,客机近机位92个。2019年9月25日,北京大兴国际机场正式投入运营. 据调查,10月大兴机场载客量约为112万人,12月载客量约为175万人,若10月到12月载客量的月增长率相同,求每月载客量的平均月增长率?23. 第二十四届冬季奥林匹克运动会将于2022年在北京市和张家口市举行.为了调查学生对冬奥知识的了解情况,从甲、乙两校各随机抽取20名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.a.甲校20名学生成绩的频数分布表和频数分布直方图如下:
甲校学生样本成绩频数分布表
成绩m(分)
频数(人数)
频率
1
0.05
c
0.10
3
0.15
a
b
6
0.30
合计
20
1.0
表1

图1
b.甲校成绩在 的这一组的具体成绩是:81 81 89 83 89 82 83 89
c.甲、乙两校成绩的平均分、中位数、众数、方差如下:
学校
平均分
中位数
众数
方差
甲
84
n
89
129.7
乙
84.2
85
85
138.6
表2
根据以上图表提供的信息,解答下列问题:
(1)、表1中a=;表2中的中位数n =;(2)、补全图1甲校学生样本成绩频数分布直方图;(3)、在此次测试中,某学生的成绩是84分,在他所属学校排在前10名,由表中数据可知该学生是校的学生(填“甲”或“乙”),理由是;(4)、假设甲校1000名学生都参加此次测试,若成绩80分及以上为优秀,估计成绩优秀的学生人数为人.24. 小明租用共享单车从家出发,匀速骑行到相距2400米的邮局办事.小明出发的同时,他的爸爸以每分钟100米的速度从邮局沿同一条道路步行回家,小明在邮局停留了2分钟后沿原路按原速返回.设他们出发后经过t(分)时,小明与家之间的距离为s1(米),小明爸爸与家之间的距离为s2(米),图中折线OABD,线段EF分别表示s1 , s2与t之间的函数关系的图象.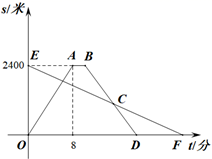 (1)、求s1与t之间的函数表达式;(2)、小明从家出发,经过分在返回途中追上爸爸.25. 如果关于 的一元二次方程 有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,研究发现了此类方程的一般性结论:设其中一根为 ,则另一个根为 ,因此 ,所以有 ;我们记“ ”即 时,方程 为倍根方程;
(1)、求s1与t之间的函数表达式;(2)、小明从家出发,经过分在返回途中追上爸爸.25. 如果关于 的一元二次方程 有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,研究发现了此类方程的一般性结论:设其中一根为 ,则另一个根为 ,因此 ,所以有 ;我们记“ ”即 时,方程 为倍根方程;下面我们根据此结论来解决问题:
(1)、方程① ;方程② ;方程③ 这几个方程中,是倍根方程的是(填序号即可);(2)、若 是倍根方程,则 的值为;26. 有这样一个问题:探究函数 的图象与性质.小华根据学习函数的经验,对函数 的图象与性质进行了探究.下面是小华的探究过程,请补充完整:(1)、函数 的自变量x的取值范围是;(2)、下表是y与x的几组对应值.m的值为;x
-2
-1
1
2
3
4
…
y
0
m
1
…
(3)、如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;(4)、结合函数的图象,写出该函数的一条性质: .(5)、结合函数图象估计 的解的个数为个. 27. 在平面直角坐标系xOy中,点P的坐标为(a,b),点P的“关联点”P’的坐标定义如下:当 时,P’点坐标为(b,a);当 时,P’点坐标为(-a,-b).(1)、写出A(5,3)的变换点坐标 , B(1,6)的变换点坐标 , C(-2,4)的变换点坐标;(2)、如果直线l: 上所有点的关联点组成一个新的图形,记作图形W,请画出图形W;(3)、在(2)的条件下,若直线y=kx-1(k≠0)与图形W有两个交点,请直接写出k的取值范围.
27. 在平面直角坐标系xOy中,点P的坐标为(a,b),点P的“关联点”P’的坐标定义如下:当 时,P’点坐标为(b,a);当 时,P’点坐标为(-a,-b).(1)、写出A(5,3)的变换点坐标 , B(1,6)的变换点坐标 , C(-2,4)的变换点坐标;(2)、如果直线l: 上所有点的关联点组成一个新的图形,记作图形W,请画出图形W;(3)、在(2)的条件下,若直线y=kx-1(k≠0)与图形W有两个交点,请直接写出k的取值范围.