广东省韶关市2020年中考数学模拟试卷
试卷更新日期:2020-06-19 类型:中考模拟
一、选择题
-
1. 已知图中所有的小正方形都全等,若在图中再添加一个全等的小正方形得到新的图形,使新图形是中心对称图形,则正确的添加方案是( )
 A、
A、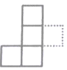 B、
B、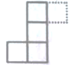 C、
C、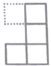 D、
D、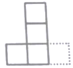 2. 截至北京时间2020年4月14日7时30分,全球新冠肺炎确诊病例已超200万例,达2019320例.将数字“2019320”用科学记数法表示为( )A、0.201932×107 B、2.01932×106 C、20.1932×105 D、201.932×1043. 下列计算正确的是( )A、a2·a3=a6 B、3a2-a2=2 C、a6÷a2=a3 D、(-2a)²=4a24. 不等式5x-2>3(x+1)的最小整数解为( )A、3 B、2 C、1 D、-15. 已知一组数据5,4,x,3,9的平均数为5,则这组数据的中位数是( )A、3 B、4 C、5 D、96. 若关于x的一元二次方程x2-2x+m=0有实数根,则实数m的取值范围是( )A、m<1 B、m≤1 C、m>1 D、m≥l7. 在同一平面直角坐标系中,函数y=kx+1(k≠0)和y= (k≠0)的图象大致是( )A、
2. 截至北京时间2020年4月14日7时30分,全球新冠肺炎确诊病例已超200万例,达2019320例.将数字“2019320”用科学记数法表示为( )A、0.201932×107 B、2.01932×106 C、20.1932×105 D、201.932×1043. 下列计算正确的是( )A、a2·a3=a6 B、3a2-a2=2 C、a6÷a2=a3 D、(-2a)²=4a24. 不等式5x-2>3(x+1)的最小整数解为( )A、3 B、2 C、1 D、-15. 已知一组数据5,4,x,3,9的平均数为5,则这组数据的中位数是( )A、3 B、4 C、5 D、96. 若关于x的一元二次方程x2-2x+m=0有实数根,则实数m的取值范围是( )A、m<1 B、m≤1 C、m>1 D、m≥l7. 在同一平面直角坐标系中,函数y=kx+1(k≠0)和y= (k≠0)的图象大致是( )A、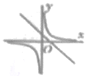 B、
B、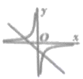 C、
C、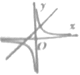 D、
D、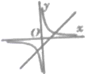 8.
8.如图,C岛在A岛的北偏东45°方向,C岛在B岛的北偏西25°方向,则从C岛看A、B两岛的视角∠ACB的度数是( )
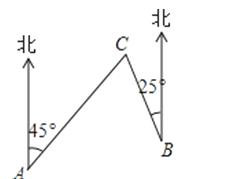 A、70° B、20° C、35° D、110°9. 如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点0.下列结论:
A、70° B、20° C、35° D、110°9. 如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点0.下列结论:①∠DOC=90°,②OC=OE,③tan∠OCD= ,④S△ODC=S四边形BEOF中,正确的有( )
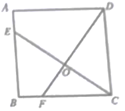 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
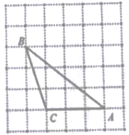
10. 如果一个正多边形的每个外角都等于72°,那么它是正边形。11. 分解因式:m²-4m+4=。12. 已知a是方程2x2=x+4的一个根,则代数式4a2-2a的值是。13. 若一个圆锥的主视图是一个腰长为6cm,底边长为2cm的等腰三角形,则这个圆锥的侧面积为cm²。14. 已知实数x,y满足 +|y-5|=0,则xy的值是。15. 如图,在6×6的正方形网格中,△ABC的顶点都在小正方形的顶点上,则cos∠BAC的值是。
 16. 如图,在平面直角坐标系中,△ABC, △A1B1C1 , △A2B2C2 , △A3B3C3 , …, △AnBnCn都是等腰直角三角形,点B,B1 , B2 , B3 , …,Bn都在x轴上,点B1与原点重合,点A,C1 , C2 , C3…,Cn都在直线l:y= 上,点C在y轴上,AB∥A1B1∥A2B2∥A3B3∥…∥AnBn∥y轴,AC∥A1C1∥A2C2∥A3C3∥…∥AnCn∥x轴,若点A的横坐标为-1,则点Cn的纵坐标是。
16. 如图,在平面直角坐标系中,△ABC, △A1B1C1 , △A2B2C2 , △A3B3C3 , …, △AnBnCn都是等腰直角三角形,点B,B1 , B2 , B3 , …,Bn都在x轴上,点B1与原点重合,点A,C1 , C2 , C3…,Cn都在直线l:y= 上,点C在y轴上,AB∥A1B1∥A2B2∥A3B3∥…∥AnBn∥y轴,AC∥A1C1∥A2C2∥A3C3∥…∥AnCn∥x轴,若点A的横坐标为-1,则点Cn的纵坐标是。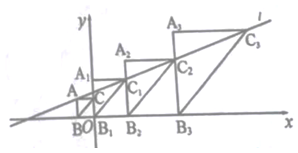
三、解答题(一)
-
17. 计算:π0+ -|-4|18. 先化简,再求值: ,其中x= +1。19. 如图,在△ABC中,∠ABC=80°,∠BAC=40°。
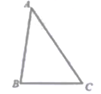 (1)、尺规作图:作线段AB的垂直平分线DE,分别与AC、AB交于点D、E;(保留作图痕迹,不要求写作法)(2)、连结BD,求证:△ABC∽△BDC。
(1)、尺规作图:作线段AB的垂直平分线DE,分别与AC、AB交于点D、E;(保留作图痕迹,不要求写作法)(2)、连结BD,求证:△ABC∽△BDC。四、解答题(二)
-
20. 某地区为进一步发展基础教育,自2017年以来加大了教育经费的投人,2017年该地区投人教育经费5000万元,2019年投人教育经费7200万元。(1)、求该地区投人教育经费的年平均增长率;(2)、若该地区教育经费的投人还将保持相同的年平均增长率,则2020年该地区投入教育经费为多少万元?21. 如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上。
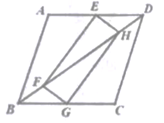 (1)、求证:BG=DE;(2)、若E为AD的中点,FH=2,求菱形ABCD的周长。22. 今年国内猪肉价格受非洲猪瘟疫情影响,有较大幅度的上升,为了解某地区养殖户受疫情影响的情况,随机抽取了部分养殖户进行了调查(把调查结果分为四个等级:A级:非常严重;B级:严重;C级:一般;D级:没有感染),并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解决下列问题:
(1)、求证:BG=DE;(2)、若E为AD的中点,FH=2,求菱形ABCD的周长。22. 今年国内猪肉价格受非洲猪瘟疫情影响,有较大幅度的上升,为了解某地区养殖户受疫情影响的情况,随机抽取了部分养殖户进行了调查(把调查结果分为四个等级:A级:非常严重;B级:严重;C级:一般;D级:没有感染),并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解决下列问题: (1)、本次抽样调查的养殖户的总户数是 ,把图2条形统计图补充完整;(2)、若该地区养殖户共有1500户,求受影响非常严重与严重的养殖户一共有多少户?(3)、某调研单位想从5户养殖户(分别记为a,b,e,d,e)中随机选取两户,进一步跟踪监测病毒传播情况,请用列表或画树状图的方法求出选中养殖户e的概率。
(1)、本次抽样调查的养殖户的总户数是 ,把图2条形统计图补充完整;(2)、若该地区养殖户共有1500户,求受影响非常严重与严重的养殖户一共有多少户?(3)、某调研单位想从5户养殖户(分别记为a,b,e,d,e)中随机选取两户,进一步跟踪监测病毒传播情况,请用列表或画树状图的方法求出选中养殖户e的概率。五、解答题(三) (本大题2小题,每小题10分,共20分)
-
23. 如图,AB是⊙O的直径,弦CD⊥AB于点E,点F是⊙O上一点,且 ,连接FB,FD,FD交AB于点N。
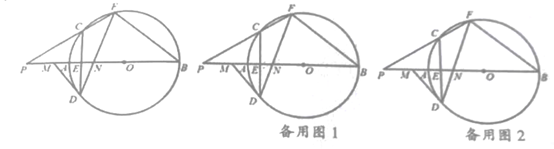 (1)、若AE=1,CD=6,求⊙O的半径长;(2)、求证:△BNF是等腰三角形;(3)、连接FC并延长,交BA的延长线于点P,过点D作⊙O的切线,交BP于点M。求证:ON·OP=OE·OM。24. 如图,在平面直角坐标系中,抛物线y= x2+bx+c与x轴交于B,C两点,与y轴交于点A,直线y= x+2经过A,C两点,抛物线的对称轴与x轴交于点D,直线MN与对称轴交于点G,与抛物线交于M,N两点(点N在对称轴右侧),且MN∥x轴,MN=7。
(1)、若AE=1,CD=6,求⊙O的半径长;(2)、求证:△BNF是等腰三角形;(3)、连接FC并延长,交BA的延长线于点P,过点D作⊙O的切线,交BP于点M。求证:ON·OP=OE·OM。24. 如图,在平面直角坐标系中,抛物线y= x2+bx+c与x轴交于B,C两点,与y轴交于点A,直线y= x+2经过A,C两点,抛物线的对称轴与x轴交于点D,直线MN与对称轴交于点G,与抛物线交于M,N两点(点N在对称轴右侧),且MN∥x轴,MN=7。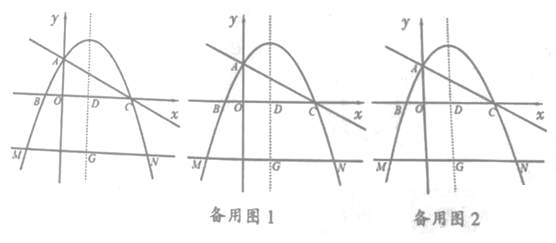 (1)、求此抛物线的解析式;(2)、求点N的坐标;(3)、若过点A的直线AF与抛物线交于点F,当tan∠FAC= 时,请直接写出点F的坐标;(4)、过点D作直线AC的垂线,交AC于点H,交y轴于点K,连接CN,△AHK沿射线AC以每秒1个单位长度的速度移动,移动过程中△AHK与四边形DGNC产生重叠,设重叠面积为S,移动时间为t(0≤t≤ ),求S与t的函数关系式。
(1)、求此抛物线的解析式;(2)、求点N的坐标;(3)、若过点A的直线AF与抛物线交于点F,当tan∠FAC= 时,请直接写出点F的坐标;(4)、过点D作直线AC的垂线,交AC于点H,交y轴于点K,连接CN,△AHK沿射线AC以每秒1个单位长度的速度移动,移动过程中△AHK与四边形DGNC产生重叠,设重叠面积为S,移动时间为t(0≤t≤ ),求S与t的函数关系式。