广东省2020年中考数学模拟试卷
试卷更新日期:2020-06-19 类型:中考模拟
一、选择题
-
1. 在0,-(-2),- , 中,是负数的是( )A、0 B、-(-2) C、- D、2. 计算 的结果是( )A、 B、 C、 D、3. 下列几何体中,三视图有两个相同,另一个不同的是( )
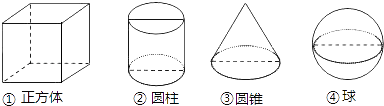 A、①② B、②③ C、②④ D、③④4. 根据安徽省公布的十三五铁路建设规划,到2020年全省铁路建设总投资4370亿元.其中4370亿用科学记数法表示为( )A、4.37×1011 B、43.7×1010 C、4.37×103 D、0.437×10125. 已知:如图,AB∥CD∥EF,∠ABC=50°,∠CEF=150°,则∠BCE的值为( )
A、①② B、②③ C、②④ D、③④4. 根据安徽省公布的十三五铁路建设规划,到2020年全省铁路建设总投资4370亿元.其中4370亿用科学记数法表示为( )A、4.37×1011 B、43.7×1010 C、4.37×103 D、0.437×10125. 已知:如图,AB∥CD∥EF,∠ABC=50°,∠CEF=150°,则∠BCE的值为( )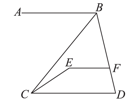 A、50° B、30° C、20° D、60°6. 如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,半径OA交小圆于点D,若OD=2,tan∠OAB=
A、50° B、30° C、20° D、60°6. 如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,半径OA交小圆于点D,若OD=2,tan∠OAB=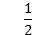 ,则AB的长是( )
,则AB的长是( ) 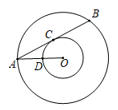 A、4 B、 C、8 D、7. 已知一组数据5,8,8,9,10,以下说法错误的是( )A、平均数是8 B、众数是8 C、中位数是8 D、方差是88. 受新冠肺炎疫情影响,某企业生产总值从元月份的300万元,连续两个月降至260万元,设平均降低率为x,则可列方程( )A、300(1-x)2=260 B、300(1-x2)=260 C、300(1-2x)=260 D、300(1+x)2=2609. 如图,O为矩形ABCD内一点,满足OD=OC,若点O到边AB的距离为d,到边DC的距离为3d,且OB=2d,则矩形ABCD的对角线的长为( )
A、4 B、 C、8 D、7. 已知一组数据5,8,8,9,10,以下说法错误的是( )A、平均数是8 B、众数是8 C、中位数是8 D、方差是88. 受新冠肺炎疫情影响,某企业生产总值从元月份的300万元,连续两个月降至260万元,设平均降低率为x,则可列方程( )A、300(1-x)2=260 B、300(1-x2)=260 C、300(1-2x)=260 D、300(1+x)2=2609. 如图,O为矩形ABCD内一点,满足OD=OC,若点O到边AB的距离为d,到边DC的距离为3d,且OB=2d,则矩形ABCD的对角线的长为( )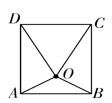 A、2d B、d C、3d D、d10. 已知抛物线y=ax2-bx和直线y=bx+a在同一坐标系内的图象如图所示,
A、2d B、d C、3d D、d10. 已知抛物线y=ax2-bx和直线y=bx+a在同一坐标系内的图象如图所示,其中正确的是( )
A、 B、
B、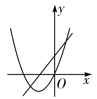 C、
C、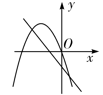 D、
D、
二、填空题
-
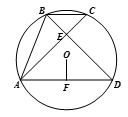
11. 计算 -3 的结果是.12. 因式分解: =.13. 如图,△ABC内接于⊙O,BD⊥AC于点E,连接AD,OF⊥AD于点F,∠D=45°.若OF=1,则BE的长为.
 14. 对于一个函数,如果它的自变量x与对应的函数值y满足:当-1≤x≤1时,-1≤y≤1,则称这个函数为“闭函数”.例如:y=x,y=-x均是“闭函数”.已知y=ax2+bx+c(a≠0)是“闭函数”,且抛物线经过点A(1,-1)和点B(-1,1),则a的取值范围是.
14. 对于一个函数,如果它的自变量x与对应的函数值y满足:当-1≤x≤1时,-1≤y≤1,则称这个函数为“闭函数”.例如:y=x,y=-x均是“闭函数”.已知y=ax2+bx+c(a≠0)是“闭函数”,且抛物线经过点A(1,-1)和点B(-1,1),则a的取值范围是.三、(本大题共2小题,每小题8分,满分16分)
-
15. 计算:| -2|+2sin60°+(π-1)0+16. 观察以下等式:
第1个等式: ,第2个等式: ,
第3个等式: ,第4个等式: …
按照以上规律,解决下列问题:
(1)、写出第5个等式;(2)、写出你猜想的第n(n为正整数)个等式(用含n的等式表示),并证明.四、(本大题共2小题,每小题8分,满分16分)
-
17. 平面直角坐标系中,△ABC的顶点坐标分别为A(2,-2),B(3,-4),C(6,-3).
①画出将△ABC向上平移6个单位后得到的△A1B1C1;
②以点M(1,2)为位似中心,在网格中画出与△A1B1C1位似的图形△A2B2C2 , 且使得△A2B2C2与△A1B1C1的相似比为2:1.
18. 合肥市某医院计划选购A,B两种防护服.已知A防护服每件价格是B防护服每件价格的2倍,用80000元单独购买A防护服比用80000元单独购买B防护服要少50件.如果该医院计划购买B防护服的件数比购买A防护服件数的2倍多8件,且用于购买A,B两种防护服的总经费不超过320000元,那么该医院最多可以购买多少件B防护服?五、(本大题共2小题,每小题10分,满分20分)
-
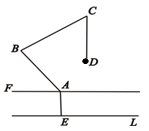
19. 如图,科博会上某公司展示了研发的绘图智能机器人,该机器人由机座、手臂和末端操作器三部分组成,底座AE⊥直线EL且AE=25 cm,手臂AB=BC=60 cm,末端操作器CD=35 cm,AF∥直线EL.当机器人运作时,∠BAF=45°,∠ABC=75°,∠BCD=60°,求末端操作器节点D到地面直线EL的距离.(结果保留根号)
 20. 如图,AB是⊙O的直径,弦CD⊥AB于点E,且CD=24,点M在⊙O上,MD经过圆心O,连接MB.
20. 如图,AB是⊙O的直径,弦CD⊥AB于点E,且CD=24,点M在⊙O上,MD经过圆心O,连接MB.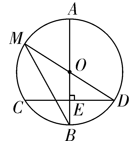 (1)、若BE=8,求⊙O的半径;(2)、若∠DMB=∠D,求线段OE的长.
(1)、若BE=8,求⊙O的半径;(2)、若∠DMB=∠D,求线段OE的长.六、(本题满分12分)
-
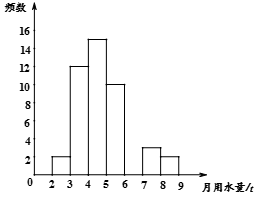
21. 小王在一次社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了若干户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如下图所示).(1)、请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量
(单位:t)
频数
百分比
2≤x<3
2
4%
3≤x<4
12
24%
4≤x<5
5≤x<6
10
20%
6≤x<7
12%
7≤x<8
3
6%
8≤x<9
2
4%
(2)、如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你估计总体小王所居住的小区中等用水量家庭大约有多少户?(3)、从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,试求抽取出的2个家庭来自不同范围的概率.七、(本题满分12分)
-
22. 建材市场为某工厂代销一种建筑材料.当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7.5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其他费用100元.(1)、当每吨售价是240元时,计算此时的月销售量;(2)、为进一步推广品牌,尽可能的扩大销量,当每吨材料售价为多少时,该经销店月利润为9000元?(3)、有人说“当月利润最大时,月销售额也最大.”你认为对吗?请说明理由.
八、(本题满分14分)
-
23. 如图1,在△ABC中,∠ACB=90°,AC=BC,D为AB上一点,连接CD,将CD绕点C 顺时针旋转90°至CE,连接AE.
 (1)、求证:△BCD≌△ACE;(2)、如图2,连接ED,若CD= ,AE=1,求AB的长;(3)、如图3,若点F为AD的中点,分别连接EB和CF,求证:CF⊥EB.
(1)、求证:△BCD≌△ACE;(2)、如图2,连接ED,若CD= ,AE=1,求AB的长;(3)、如图3,若点F为AD的中点,分别连接EB和CF,求证:CF⊥EB.
-
-