吉林省五地六市联盟2018-2019学年高一下学期数学期末考试试卷

试卷更新日期：2020-06-18 类型：期末考试

进入出卷网下载

一、单选题

1. 下列命题中正确的是（）

A、 $\overset{⇀}{O A} - \overset{⇀}{O B} = \overset{⇀}{A B}$ B、 $\overset{⇀}{A B} + \overset{⇀}{B A} = 0$ C、 $0 \cdot \overset{⇀}{A B} = 0$ D、 $\overset{⇀}{A B} + \overset{⇀}{B C} - \overset{⇀}{D C} = \overset{⇀}{A D}$

查看试题解析
2. 下面一段程序执行后的结果是（）
$a = 2$

$a = a * 2$

$a = a + 2$ $P R I N T$ $a$ $E N D$

A、6 B、4 C、8 D、10

查看试题解析
3. 若 $a > b$ , 则下列不等式正确的是（）

A、 $a^{2} > b^{2}$ B、 $a c > b c$ C、 $a - c > b - c$ D、 $a c^{2} > b c^{2}$

查看试题解析
4. 已知 $Δ A B C$ 中， $a = \sqrt{2}$ ， $b = \sqrt{3}$ ， $B = 60^{\circ}$ ，那么角A等于（）

A、 $135^{\circ}$ B、 $45^{\circ}$ C、 $135^{\circ}$ 或 $45^{\circ}$ D、 $90^{\circ}$

查看试题解析
5. 从一批产品中取出三件产品，设事件A为“三件产品全不是次品”，事件 $B$ 为“三件产品全是次品”，事件C为“三件产品不全是次品”，则下列结论正确的是（）

A、事件A与C互斥 B、事件B与C互斥 C、任何两个事件均互斥 D、任何两个事件均不互斥

查看试题解析
6. 若 x、y 满足约束条件 ${\begin{cases} x \geq 0 \\ x + 2 y \geq 3 \\ 2 x + y \leq 3 \end{cases}$ ，则 z=x-y 的最小值是（）

A、0 B、 $- 3$ C、 $\frac{3}{2}$ D、3

查看试题解析
7. 在长为12cm的线段AB上任取一点C．现作一矩形，邻边长分别等于线段AC，CB的长，则该矩形面积大于20cm²的概率为（）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{4}{5}$

查看试题解析
8. 某产品的广告费用x与销售额y的统计数据如下表：

广告费用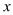（万元）

4

2

3

5

销售额（万元）

49

26

39

54

根据上表可得回归方程 $\hat{y} = \hat{b} x + \hat{a}$ 中的 $\hat{b}$ 为9.4，据此模型预报广告费用为6万元时销售额为（）

A、63.6万元 B、65.5万元 C、67.7万元 D、72.0万元

查看试题解析
9. 数列 ${a_{n}}$ 中，若 $a_{1} = 2$ ， $a_{n + 1} = 2 a_{n} + 3$ ，则 $a_{10} =$ （）

A、29 B、2563 C、2569 D、2557

查看试题解析
10. 在 $Δ A B C$ 中，已知a、b、c分别是角A、B、C的对边，若 $\frac{a}{b} = \frac{\cos B}{\cos A}$ ，则 $△ A B C$ 的形状为（）

A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、等腰三角形或直角三角形

查看试题解析
11. 若正数x，y满足x+3y=5xy，则3x+4y的最小值是（）

A、 $\frac{24}{5}$ B、 $\frac{28}{5}$ C、5 D、6

查看试题解析
12. 在 $Δ A B C$ 中， $A C = 6 ， B C = 7 ， \cos A = \frac{1}{5}$ ， $O$ 是 $Δ A B C$ 的内心，若 $\overset{⇀}{O P} = x \overset{⇀}{O A} + y \overset{⇀}{O B}$ ，其中 $0 \leq x \leq 1 ， 1 \leq y \leq 2$ ，动点p的轨迹所覆盖的面积为（）

A、 $\frac{10}{3} \sqrt{6}$ B、 $\frac{5}{3} \sqrt{6}$ C、 $\frac{10}{3}$ D、 $\frac{20}{3}$

查看试题解析

二、填空题

13. 若采用系统抽样的方法从420人中抽取21人做问卷调查，为此将他们随机编号为1,2，…，420，则抽取的21人中，编号在区间[241,360]内的人数是

查看试题解析
14. 如图是甲、乙两人在10天中每天加工零件个数的茎叶图，若这10天甲加工零件个数的中位数为a，乙加工零件个数的平均数为b，则 $a + b =$ .

查看试题解析
15. 执行如图所示的程序框图，则输出结果 $S =$ .

查看试题解析
16. 已知数列 ${a_{n}}$ 的前 $n$ 项和是 $S_{n}$ ，且 $4 S_{n} = {(a_{n} + 1)}^{2}$ ，则 $a_{n} =$ .（写出两个即可）

查看试题解析

三、解答题

17. 从甲、乙、丙、丁四个人中选两名代表，求：

(1)、甲被选中的概率；

(2)、丁没被选中的概率.

查看试题解析
18. 已知 $\vec{a}, \vec{b}, \vec{c}$ 是同一平面内的三个向量， $\vec{a} = (1, 2)$ ；

(1)、若 $| \vec{c} | = 2 \sqrt{5}$ ，且 $\vec{c} ∥ \vec{a}$ ，求 $\vec{c}$ 的坐标；

(2)、若 $| \vec{b} | = \frac{\sqrt{5}}{2}$ ，且 $\vec{a} + 2 \vec{b}$ 与 $2 \vec{a} - \vec{b}$ 垂直，求 $\vec{a}$ 与 $\vec{b}$ 的夹角 $θ$ .

查看试题解析
19. 已知a，b，c分别为 $Δ A B C$ 三个内角A，B，C的对边， $\frac{\cos B}{\cos A} + \frac{b}{a} = \frac{2 c}{a}$ .

(1)、求角A的大小；

(2)、若 $a = 2$ ， $Δ A B C$ 的面积为 $\sqrt{3}$ ，求边b，c.

查看试题解析

20. 某高校在2012年的自主招生考试成绩中随机抽取

100

名中学生的笔试成绩，按成绩分组，得到的频率分布表如表所示．

组号	分组	频数	频率
第1组	$[160 ， 165)$	5	$0.050$
第2组	$[165 ， 170)$	①	$0.350$
第3组	$[170 ， 175)$	30	②
第4组	$[175 ， 180)$	20	$0.200$
第5组	$[180 ， 185)$	10	$0.100$

(1)、请先求出频率分布表中

① ， ②

位置的相应数据，再完成频率分布直方图；

(2)、为了能选拔出最优秀的学生，高校决定在笔试成绩高的第

3 ， 4 ， 5

组中用分层抽样抽取6名学生进入第二轮面试，求第3、4、5组每组各抽取多少名学生进入第二轮面试；

(3)、在（2）的前提下，学校决定在

6

名学生中随机抽取

2

名学生接受

A

考官进行面试，求：第

4

组至少有一名学生被考官

A

面试的概率．

查看试题解析

21. 已知等差数列 ${a_{n}}$ 满足 $a_{3} = 5$ ， $a_{6} = a_{4} + 4$ ，公比为正数的等比数列 ${b_{n}}$ 满足 $b_{2} = 1$ ， $b_{3} b_{5} = \frac{1}{16}$ .

(1)、求数列 ${a_{n}}$ ， ${b_{n}}$ 的通项公式；

(2)、设 $c_{n} = \frac{a_{n} b_{n}}{2}$ ，求数列 ${c_{n}}$ 的前 $n$ 项和 $T_{n}$ .

查看试题解析
22. 已知函数 $f (x) = (m + 1) x^{2} - m x + m - 1$ （ $m \in R$ ）．

(1)、若不等式 $f (x) < 0$ 的解集为 $\emptyset$ ，求m的取值范围；

(2)、当 $m > - 2$ 时，解不等式 $f (x) \geq m$ ；

(3)、若不等式 $f (x) \geq 0$ 的解集为 $D$ ，若 $[- 1 ， 1] \subseteq D$ ，求m的取值范围．

查看试题解析

广告费用（万元）	4	2	3	5
销售额（万元）	49	26	39	54