浙江省金华市2020年数学中考仿真模拟卷
试卷更新日期：2020-06-18 类型：中考模拟
一、选择题（共10小题，满分30分，每小题3分）
-
1. 向北行驶3km，记作+3km，向南行驶2km记作（ ）A、+2 km B、﹣2 km C、+3 km D、﹣3 km2. 计算a6÷a2的结果是（ ）A、a2 B、a3 C、a4 D、a53. 若分式 的值为0，则x的值为（ ）A、3 B、﹣3 C、3或﹣3 D、04. 有下列长度的三条线段，其中能组成三角形的是（ ）A、3、5、10 B、10、4、6 C、3、1、1 D、4、6、95. 从一个物体的不同方向看到的是如图所示的三个图形，则该物体的形状为（ ）
A、圆柱 B、棱柱 C、球 D、圆锥6. 在一个不透明的口袋中装有2个红球和若干个黑球，这些球除颜色外其他都相同，将袋中的球搅匀，从中任意摸出一个球，是黑球的概率是 ，则袋中原有黑球（ ）A、2 B、3 C、4 D、67. 在如图所示的网格中有M，N，P，Q四个点，鹏鹏在该网格中建立了一个平面直角坐标系，然后得到点M的坐标为（﹣3，﹣1），点P的坐标为（0，﹣2），则点N和点Q的坐标分别为（ ）
A、（2，1），（1，﹣2） B、（1，1），（2，﹣2） C、（2，1），（﹣1，2） D、（1，1），（﹣2，2）8. 若关于x的不等式组 的解集为x＜3，则k的取值范围为（ ）A、k＞1 B、k＜1 C、k≥1 D、k≤19. 如图，将直角三角形ABC（∠BAC＝90°）绕点A逆时针旋转一定角度得到直角三角形ADE，若∠CAE＝65°，若∠AFB＝90°，则∠D的度数为（ ）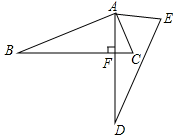
A、60° B、35° C、25° D、15°10. 如图①，一个立方体铁块放置在圆柱形水槽内，现以每秒固定的流量往水槽中注水，28秒时注满水槽，水槽内水面的高度y（厘米）与注水时间x（秒）之间的函数图象如图②所示，则圆柱形水槽的容积（在没放铁块的情况下）是（ ）
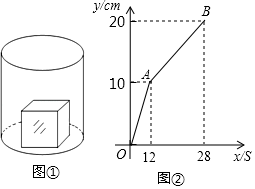A、8000cm3 B、10000 cm3 C、2000πcm3 D、3000πcm3二、填空题（共6小题，满分24分，每小题4分）
-
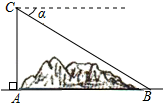
11. 分解因式：4﹣m2＝.12. 一组数据30，18，24，26，33，28的中位数是.13. 若x﹣2y＝4，则4x﹣8y﹣2＝.14. 如图，某地修建高速公路，要从A地向B地修一条隧道（点A、B在同一水平面上）为了测量A、B两地之间的距离，一架直升飞机从A地出发，垂直上升800米到达C处，在C处观察B地的俯角为α，则A、B两地之间的距离为米.
15. 如图，已知点A（2，3）和点B（0，2），点A在反比例函数y＝ 的图象上，作射线AB，再将射线AB绕点A按逆时针方向旋转45°，交反比例函数图象于点C，则点C的坐标为.
16. 如图1是小明制作的一副弓箭，点A，D分别是弓臂BAC与弓弦BC的中点，弓弦BC＝60cm.沿AD方向拉动弓弦的过程中，假设弓臂BAC始终保持圆弧形，弓弦不伸长.如图2，当弓箭从自然状态的点D拉到点D1时，有AD1＝30cm，∠B1D1C1＝120°.
(1)、图2中，弓臂两端B1 ， C1的距离为cm.(2)、如图3，将弓箭继续拉到点D2 ， 使弓臂B2AC2为半圆，则D1D2的长为cm.三、解答题（共8小题，满分66分）
-
17. 计算：4cos30°﹣ +20180+|1﹣ |
18. 解分式方程： ﹣ ＝1.
19. 随着生活水平的日益提高，人们越来越喜欢过节，节日的仪式感日渐浓烈，某校举行了“母亲节暖心特别行动”，从中随机调查了部分同学的暖心行动，并将其分为A，B，C，D四种类型（分别对应送服务、送鲜花、送红包、送话语）.现根据调查的数据绘制成如下的条形统计图和扇形统计图.请根据以上不完整的统计图提供的信息，解答下列问题：
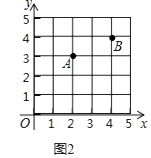
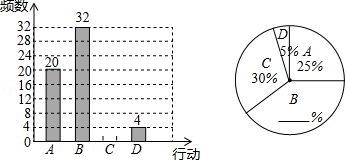(1)、该校共抽查了多少名同学的暖心行动？(2)、求出扇形统计图中扇形B的圆心角度数？(3)、若该校共有2400名同学，请估计该校进行送鲜花行动的同学约有多少名？20. 在直角坐标系中，我们把横、纵坐标都为整数的点称为整点，记顶点都是整点的三角形为整点三角形．如图，已知整点A（2，3），B（4，4），请在所给网格区域（含边界）上按要求画整点三角形．(1)、在图1中画一个△PAB，使点P的横、纵坐标之和等于点A的横坐标；
(2)、在图2中画一个△PAB，使点P，B横坐标的平方和等于它们纵坐标和的4倍．
21. 如图①，在平行四边形OABC中，以O为圆心，OA为半径的圆与BC相切于点B，与OC相交于点D.
(1)、求∠OAB的度数；
(2)、如图②，点E在⊙O上，连接CE与⊙O交于点F，若EF＝AB，求∠COE的度数.
22. 如图，正六边形ABCDEF的对称中心P在反比例函数y＝ （k＞0，x＞0）的图象上边CD在x轴上，点B在y轴上，已知CD＝4.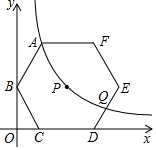
(1)、点A是否在该反比例函数的图象上？请说明理由.
(2)、若该反比例函数图象与DE交于点Q，求点Q的横坐标；
(3)、平移正六边形ABCDEF，使其一边的两个端点恰好都落在该反比例函数的图象上，试描述平移过程.
23. 如图，抛物线y＝ax2+bx（a＜0）过点E（10，0），矩形ABCD的边AB在线段OE上（点A在点B的左边），点C，D在抛物线上.设A（t，0），当t＝2时，AD＝4.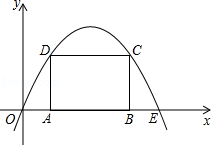
(1)、求抛物线的函数表达式.(2)、当t为何值时，矩形ABCD的周长有最大值？最大值是多少？(3)、保持t＝2时的矩形ABCD不动，向右平移抛物线.当平移后的抛物线与矩形的边有两个交点G，H，且直线GH平分矩形的面积时，求抛物线平移的距离.24. 如图1，在Rt△ABC中，∠A＝90°，AB＝AC，点D，E分别在边AB，AC上，AD＝AE，连接DC，点M，P，N分别为DE，DC，BC的中点.
(1)、观察猜想：图1中，线段PM与PN的数量关系是 ， 位置关系是；
(2)、探究证明：把△ADE绕点A逆时针方向旋转到图2的位置，连接MN，BD，CE，判断△PMN的形状，并说明理由；
(3)、拓展延伸：把△ADE绕点A在平面内自由旋转，若AD＝4，AB＝10，请直接写出△PMN面积的最大值.