浙江省嘉兴市2020年数学中考仿真模拟卷
试卷更新日期:2020-06-18 类型:中考模拟
一、一.选择题(共10小题,满分30分,每小题3分)
-
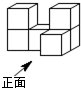
1. ﹣27的绝对值是( )A、﹣ B、 C、27 D、﹣272. 舌尖上的浪费让人触目惊心,据统计中国每年浪费的食物总量折合粮食约499.5亿千克,这个数用科学记数法应表示为( )A、4.995×1011 B、49.95×1010 C、0.4995×1011 D、4.995×10103. 如图是由完全相同的6个小正方体组成的几何体,则该几何体从上面看为( )
 A、
A、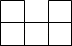 B、
B、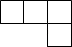 C、
C、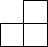 D、
D、 4. 不等式3x﹣6≥0的解集在数轴上表示正确的是( )
4. 不等式3x﹣6≥0的解集在数轴上表示正确的是( )
A、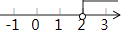 B、
B、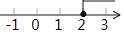 C、
C、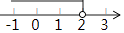 D、
D、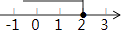 5. 已知 是方程组 的解,则a+b的值是( )A、﹣1 B、1 C、﹣5 D、56. 用配方法解方程x2﹣6x﹣4=0,下列配方正确的是( )A、(x﹣3)2=13 B、(x+3)2=13 C、(x﹣6)2=4 D、(x﹣3)2=57. 如图,有以下3个条件:①AC=AB,②AB∥CD,③∠1=∠2,从这3个条件中任选2个作为题设,另1个作为结论,则组成的命题是真命题的概率是( )
5. 已知 是方程组 的解,则a+b的值是( )A、﹣1 B、1 C、﹣5 D、56. 用配方法解方程x2﹣6x﹣4=0,下列配方正确的是( )A、(x﹣3)2=13 B、(x+3)2=13 C、(x﹣6)2=4 D、(x﹣3)2=57. 如图,有以下3个条件:①AC=AB,②AB∥CD,③∠1=∠2,从这3个条件中任选2个作为题设,另1个作为结论,则组成的命题是真命题的概率是( )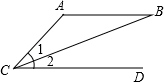 A、0 B、 C、 D、18. 如图,以菱形ABCD的顶点A为原点,直线AD为x轴建立直角坐标系,已知B点的坐标为(3,4),把菱形向上平移2个单位,那么C点平移后相应的点的坐标是( )
A、0 B、 C、 D、18. 如图,以菱形ABCD的顶点A为原点,直线AD为x轴建立直角坐标系,已知B点的坐标为(3,4),把菱形向上平移2个单位,那么C点平移后相应的点的坐标是( )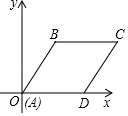 A、(8,5) B、(5,8) C、(8,6) D、(6,8)9. 如图,在矩形纸片ABCD中,已知AD=8,折叠纸片,使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )
A、(8,5) B、(5,8) C、(8,6) D、(6,8)9. 如图,在矩形纸片ABCD中,已知AD=8,折叠纸片,使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( ) A、3 B、4 C、5 D、610. 已知二次函数y=ax2+bx+c,且a>b>c,a+b+c=0,有以下四个命题,则一定正确命题的序号是( )
A、3 B、4 C、5 D、610. 已知二次函数y=ax2+bx+c,且a>b>c,a+b+c=0,有以下四个命题,则一定正确命题的序号是( )①x=1是二次方程ax2+bx+c=0的一个实数根;②二次函数y=ax2+bx+c的开口向下;③二次函数y=ax2+bx+c的对称轴在y轴的左侧;④不等式4a+2b+c>0一定成立.( )
A、①② B、①③ C、①④ D、③④二、二.填空题(共6小题,满分24分,每小题4分)
-
11. 分解因式:ab﹣b2= .12. 实数a,b,c在数轴上对应点的位置如图所示,则bca(填“>”“<”或“=”)
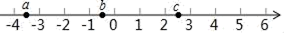 13. 如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,那么 的值等于.
13. 如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,那么 的值等于.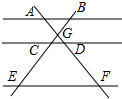 14. 一条排水管截面圆的半径为2米,∠AOB=120°,则储水部分(阴影部分)的面积是平方米.
14. 一条排水管截面圆的半径为2米,∠AOB=120°,则储水部分(阴影部分)的面积是平方米.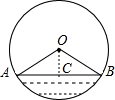 15. 某物流仓储公司用A,B两种型号的机器人搬运物品,已知A型机器人比B型机器人每小时多搬运20kg,A型机器人搬运1000kg所用时间与B型机器人搬运800kg所用时间相等,设B型机器人每小时搬运x kg物品,列出关于x的方程为.
15. 某物流仓储公司用A,B两种型号的机器人搬运物品,已知A型机器人比B型机器人每小时多搬运20kg,A型机器人搬运1000kg所用时间与B型机器人搬运800kg所用时间相等,设B型机器人每小时搬运x kg物品,列出关于x的方程为. 16. 如图1,含30°和45°角的两块三角板ABC和DEF叠合在一起,边BC与EF重合,BC=EF=12cm,点P为边BC(EF)的中点,现将三角板ABC绕点P按逆时针方向旋转角度α(如图2),设边AB与EF相交于点Q,则当a从0°到90°的变化过程中,点Q移动的路径长为(结果保留根号)
16. 如图1,含30°和45°角的两块三角板ABC和DEF叠合在一起,边BC与EF重合,BC=EF=12cm,点P为边BC(EF)的中点,现将三角板ABC绕点P按逆时针方向旋转角度α(如图2),设边AB与EF相交于点Q,则当a从0°到90°的变化过程中,点Q移动的路径长为(结果保留根号)
三、三.解答题(共8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分。)
-
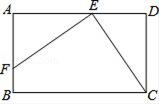
17.(1)、计算:( )2﹣2﹣1×(﹣4);(2)、化简:(m+2)(m﹣2)﹣ ×3m.18. 已知:如图,在矩形ABCD中,E为AD上一点,EF⊥CE,交AB于点F,DE=2,矩形的周长为16,且CE=EF.求AE的长.
 19. 尺规作图:已知△ABC,如图:
19. 尺规作图:已知△ABC,如图: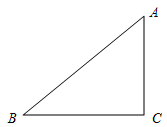 (1)、求作:△ABC的内切圆⊙O;(保留作图痕迹,不写作法)(2)、若∠C=90°,AC=3,AB=4,则△ABC的内切圆⊙O的半径为.20. 如图,在直角坐标系中,已知点B(8,0),等边三角形OAB的顶点A在反比例函数y=
(1)、求作:△ABC的内切圆⊙O;(保留作图痕迹,不写作法)(2)、若∠C=90°,AC=3,AB=4,则△ABC的内切圆⊙O的半径为.20. 如图,在直角坐标系中,已知点B(8,0),等边三角形OAB的顶点A在反比例函数y= 的图象上. (1)、求反比例函数的表达式;(2)、把△OAB向右平移a个单位长度,对应得到△O′A′B′,当这个函数图象经过△O′A′B′一边的中点时,求a的值.21. 为提高节水意识,小申随机统计了自己家7天的用水量,并分析了第3天的用水情况,将得到的数据进行整理后,绘制成如图所示的统计图.(单位:升)
的图象上. (1)、求反比例函数的表达式;(2)、把△OAB向右平移a个单位长度,对应得到△O′A′B′,当这个函数图象经过△O′A′B′一边的中点时,求a的值.21. 为提高节水意识,小申随机统计了自己家7天的用水量,并分析了第3天的用水情况,将得到的数据进行整理后,绘制成如图所示的统计图.(单位:升)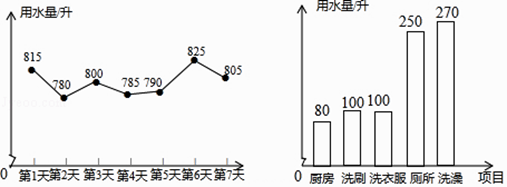 (1)、求这7天内小申家每天用水量的平均数和中位数;(2)、求第3天小申家洗衣服的水占这一天总用水量的百分比;(3)、请你根据统计图中的信息,给小申家提出一条合理的节约用水建议,并估算采用你的建议后小申家一个月(按30天计算)的节约用水量.22. 2018年10月23日,港珠澳大桥正式开通,成为横亘在伶仃洋上一道靓丽的风景.大桥主体工程隧道的东、西两端各设置了一个海中人工岛,来衔接桥梁和海底隧道,西人工岛上的A点和东人工岛上的B点间的距离约为5.6千米,点C是与西人工岛相连的大桥上的一点,A,B,C在一条直线上.如图,一艘观光船沿与大桥段垂直的方向航行,到达P点时观测两个人工岛,分别测得与观光船航向的夹角∠DPA=18°,∠DPB=53°,求此时观光船到大桥AC段的距离PD的长.(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.33,sin53°≈0.80,cos53°≈0.60,tan53°≈1.33.)
(1)、求这7天内小申家每天用水量的平均数和中位数;(2)、求第3天小申家洗衣服的水占这一天总用水量的百分比;(3)、请你根据统计图中的信息,给小申家提出一条合理的节约用水建议,并估算采用你的建议后小申家一个月(按30天计算)的节约用水量.22. 2018年10月23日,港珠澳大桥正式开通,成为横亘在伶仃洋上一道靓丽的风景.大桥主体工程隧道的东、西两端各设置了一个海中人工岛,来衔接桥梁和海底隧道,西人工岛上的A点和东人工岛上的B点间的距离约为5.6千米,点C是与西人工岛相连的大桥上的一点,A,B,C在一条直线上.如图,一艘观光船沿与大桥段垂直的方向航行,到达P点时观测两个人工岛,分别测得与观光船航向的夹角∠DPA=18°,∠DPB=53°,求此时观光船到大桥AC段的距离PD的长.(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.33,sin53°≈0.80,cos53°≈0.60,tan53°≈1.33.)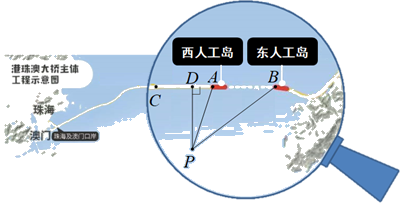 23. 已知:正方形ABCD,等腰直角三角形的直角顶点落在正方形的顶点D处,使三角板绕点D旋转.
23. 已知:正方形ABCD,等腰直角三角形的直角顶点落在正方形的顶点D处,使三角板绕点D旋转.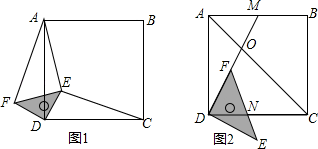 (1)、当三角板旋转到图1的位置时,猜想CE与AF的数量关系,并加以证明;(2)、在(1)的条件下,若DE=1,AE= ,CE=3,求∠AED的度数;(3)、若BC=4,点M是边AB的中点,连结DM,DM与AC交于点O,当三角板的一边DF与边DM重合时(如图2),若OF= ,求CN的长.24. 如图,已知抛物线y=ax2+bx+3(a≠0)经过点A(1,0)和点B(3,0),与y轴交于点C.
(1)、当三角板旋转到图1的位置时,猜想CE与AF的数量关系,并加以证明;(2)、在(1)的条件下,若DE=1,AE= ,CE=3,求∠AED的度数;(3)、若BC=4,点M是边AB的中点,连结DM,DM与AC交于点O,当三角板的一边DF与边DM重合时(如图2),若OF= ,求CN的长.24. 如图,已知抛物线y=ax2+bx+3(a≠0)经过点A(1,0)和点B(3,0),与y轴交于点C.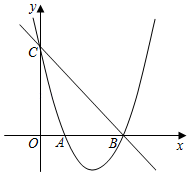 (1)、求此抛物线的解析式;(2)、若点P是直线BC下方的抛物线上一动点(不点B,C重合),过点P作y轴的平行线交直线BC于点D,设点P的横坐标为m.
(1)、求此抛物线的解析式;(2)、若点P是直线BC下方的抛物线上一动点(不点B,C重合),过点P作y轴的平行线交直线BC于点D,设点P的横坐标为m.①用含m的代数式表示线段PD的长.
②连接PB,PC,求△PBC的面积最大时点P的坐标.
(3)、设抛物线的对称轴与BC交于点E,点M是抛物线的对称轴上一点,N为y轴上一点,是否存在这样的点M和点N,使得以点C、E、M、N为顶点的四边形是菱形?如果存在,请直接写出点M的坐标;如果不存在,请说明理由.