浙江省湖州市2020年数学中考仿真卷

试卷更新日期：2020-06-18 类型：中考模拟

进入出卷网下载

一、一.选择题（本题有10小题，每小题3分，共30分。）

1. ﹣ $\frac{1}{8}$ 的倒数是（）

A、 $\frac{1}{8}$ B、﹣8 C、8 D、 $- \frac{1}{8}$

查看试题解析
2. 计算2x³•（﹣x²）的结果是（）

A、2x B、﹣2x⁵ C、2x⁶ D、x⁵

查看试题解析
3. 如图所示的几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
4. 2018年世界杯足球赛中，某国家足球队首发上场的10名队员身高（单位cm）如表：

身高

176

178

180

182

186

188

人数

1

2

3

2

1

1

则这10名队员身高的众数是（）

A、 182 B、180 C、2.5 D、3

查看试题解析
5. 如图，在△ABC中，∠B＝50°，点D在BC上，且AB＝BD，AD＝CD，则∠C的度数为（）

A、30° B、32.5° C、45° D、60°

查看试题解析
6. 如图，把△ABC纸片的∠A沿DE折叠，点A落在四边形CBDE外，则∠1、∠2与∠A的关系是（）

A、∠1+∠2＝2∠A B、∠2﹣∠A＝2∠1 C、∠2﹣∠1＝2∠A D、∠1+∠A＝ $\frac{1}{2}$ ∠2

查看试题解析
7. 如图，一次函数y₁＝x﹣1与反比例函数y₂＝ $\frac{2}{x}$ 的图象交于点A（2，1），B（﹣1，﹣2），则使y₁＞y₂的x的取值范围是（）

A、x＞2 B、x＞2 或﹣1＜x＜0 C、﹣1＜x＜2 D、x＞2 或x＜﹣1

查看试题解析
8. 某市公园的东、南、西、北方向上各有一个入口，周末佳佳和琪琪随机从一个入口进入该公园游玩，则佳佳和琪琪恰好从同一个入口进入该公园的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{4}$ C、 $\frac{1}{6}$ D、 $\frac{1}{16}$

查看试题解析
9. 如图，Rt△ABC中，∠C＝90°，用尺规作图法作出射线AE，AE交BC于点D，CD＝2，P为AB上一动点，则PD的最小值为（）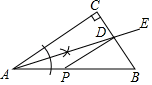

A、2 B、3 C、4 D、无法确定

查看试题解析
10. 在每个小正方形的边长为1的网格图形中，每个小正方形的顶点称为格点．从一个格点移动到与之相距 $\sqrt{5}$ 的另一个格点的运动称为一次跳马变换．例如，在4×4的正方形网格图形中（如图1），从点A经过一次跳马变换可以到达点B，C，D，E等处．现有10×10的正方形网格图形（如图2），则从该正方形的顶点M经过跳马变换到达与其相对的顶点N，最少需要跳马变换的次数是（　　）

A、6 B、7 C、8 D、9

查看试题解析

二、二.填空题（本题有6小题,每小题4分,共24分）

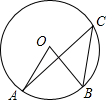
11. 因式分解：x²+6x＝．

查看试题解析
12. 代数式 $\frac{x}{x - 1}$ 有意义的x的取值范围是.

查看试题解析
13. 如图，圆心角∠AOB＝60°，则∠ACB的度数为.

查看试题解析
14. 若一个多边形的内角和等于它的外角和，则这个多边形的边数为.

查看试题解析
15. 如图，∠AOB＝30°，n个半圆依次外切，它们的圆心都在射线OA上并与射线OB相切，设半圆C₁、半圆C₂、半圆C₃…、半圆∁_n的半径分别是r₁、r₂、r₃…、r_n ，则 $\frac{r_{2013}}{r_{2012}}$ ＝.

查看试题解析
16. 如图，直线y＝ax+b与反比例函数y＝ $\frac{c}{x}$ （c＜0）的图象交于A，B两点，在反比例函数y＝ $\frac{d}{x}$ （d＞0）图象的第一象限分支上取一点C，若△ABC是以原点O为重心的等边三角形，则 $\frac{c d}{a b^{4}}$ 的值为.

查看试题解析

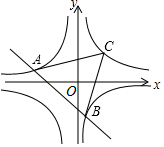
三、三.解答题（本大题共8小题，共66分.）

17. 计算：（﹣2）³×4﹣（﹣5）÷ $\frac{1}{2}$ ．

查看试题解析
18. 解方程： $\frac{x - 3}{x - 2} + 1 = \frac{3}{2 - x}$ ．

查看试题解析
19. 已知抛物线y＝a（x﹣3）²+2经过点（1，﹣2）.

(1)、求a的值.

(2)、若点A（m，y₁），（n，y₂）（m＜n＜3）都在该抛物线上，试比较y₁与y₂的大小.

查看试题解析
20. 绵阳某公司销售部统计了每个销售员在某月的销售额，绘制了如下折线统计图和扇形统计图：

设销售员的月销售额为x（单位：万元）.销售部规定：当x＜16时为“不称职”，当16≤x＜20时为“基本称职”，当20≤x＜25时为“称职”，当x≥25时为“优秀”.根据以上信息，解答下列问题：

(1)、补全折线统计图和扇形统计图；

(2)、求所有“称职”和“优秀”的销售员月销售额的中位数和众数；

(3)、为了调动销售员的积极性，销售部决定制定一个月销售额奖励标准，凡月销售额达到或超过这个标准的销售员将获得奖励.如果要使得所有“称职”和“优秀”的销售员的一半人员能获奖，月销售额奖励标准应定为多少万元（结果取整数）？并简述其理由.

查看试题解析
21. 如图，AB是⊙O的直径，CD是⊙O的弦，且CD⊥AB于点E.

(1)、求证：∠BCO＝∠D；

(2)、若CD＝2 $\sqrt{3}$ ，AE＝1，求劣弧BD的长.

查看试题解析
22. 小明从家去李宁体育馆游泳，同时，妈妈从李宁体育馆以50米/分的速度回家，小明到体育馆后发现要下雨，立即返回，追上妈妈后，小明以250米/分的速度回家取伞，立即又以250米/分的速度折回接妈妈，并一同回家.如图是两人离家的距离y（米）与小明出发的时间x（分）之间的函数图象.

（注：小明和妈妈始终在同一条笔直的公路上行走，图象上A、C、D、F四点在一条直线上）

(1)、求线段OB及线段AF的函数表达式；

(2)、求C点的坐标及线段BC的函数表达式；

(3)、当x为时，小明与妈妈相距1500米；

(4)、求点D坐标，并说明点D的实际意义.

查看试题解析
23. △ABC和△DEF是两个全等的等腰直角三角形，∠BAC＝∠EDF＝90°，△EDF的顶点E与△ABC的斜边BC的中点重合，将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q.

(1)、如图①，当点Q在线段AC上，且AP＝AQ时，求证：△BPE≌△CQE；

(2)、如图②，当点Q在线段CA的延长线上时，求证：△BPE∽△CEQ；

(3)、在（2）的条件下，BP＝2，CQ＝9，则BC的长为.

查看试题解析
24. 如图，已知抛物线y＝ax²+bx+3（a≠0）经过点A（1，0）和点B（3，0），与y轴交于点C.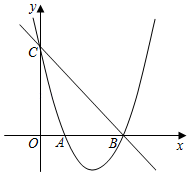

(1)、求此抛物线的解析式；

(2)、若点P是直线BC下方的抛物线上一动点（不点B，C重合），过点P作y轴的平行线交直线BC于点D，设点P的横坐标为m.
①用含m的代数式表示线段PD的长.

②连接PB，PC，求△PBC的面积最大时点P的坐标.

(3)、设抛物线的对称轴与BC交于点E，点M是抛物线的对称轴上一点，N为y轴上一点，是否存在这样的点M和点N，使得以点C、E、M、N为顶点的四边形是菱形？如果存在，请直接写出点M的坐标；如果不存在，请说明理由.

查看试题解析

身高	176	178	180	182	186	188
人数	1	2	3	2	1	1