浙江省丽水市中考数学2020年数学中考仿真模拟卷
试卷更新日期:2020-06-18 类型:中考模拟
一、一.选择题(共10小题,满分30分,每小题3分)
-
1. 四个有理数﹣1,2,0,﹣3,其中最小的是( )A、﹣1 B、2 C、0 D、﹣32. 计算a6÷a2的结果是( )A、a2 B、a3 C、a4 D、a53. 下列几何体中,主视图和俯视图都是长方形的是( )A、
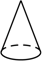 B、
B、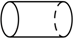 C、
C、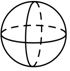 D、
D、 4. 在一周内,小明坚持自测体温,每天3次.测量结果统计如下表:
4. 在一周内,小明坚持自测体温,每天3次.测量结果统计如下表:体温(℃)
36.1
36.2
36.3
36.4
36.5
36.6
36.7
次数
2
3
4
6
3
1
2
则这些体温的中位数是( )
A、36.2℃ B、36.3℃ C、36.4℃ D、36.5℃5. 化简 + 的结果是( )A、x B、x﹣1 C、﹣x D、x+16. 已知关于x的方程2x﹣a=x﹣1的解是非负数,则a的取值范围为( )A、a≥1 B、a>1 C、a≤1 D、a<17. 如图,在▱ABCD中,若∠A+∠C=130°,则∠D的大小为( ) A、100° B、105° C、110° D、115°8. 将抛物线y=2x2向左平移3个单位得到的抛物线的解析式是( )A、y=2x2+3 B、y=2x2﹣3 C、y=2(x+3)2 D、y=2(x﹣3)29. 如图,将直角三角形ABC(∠BAC=90°)绕点A逆时针旋转一定角度得到直角三角形ADE,若∠CAE=65°,若∠AFB=90°,则∠D的度数为( )
A、100° B、105° C、110° D、115°8. 将抛物线y=2x2向左平移3个单位得到的抛物线的解析式是( )A、y=2x2+3 B、y=2x2﹣3 C、y=2(x+3)2 D、y=2(x﹣3)29. 如图,将直角三角形ABC(∠BAC=90°)绕点A逆时针旋转一定角度得到直角三角形ADE,若∠CAE=65°,若∠AFB=90°,则∠D的度数为( )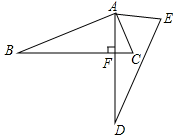 A、60° B、35° C、25° D、15°10. 从甲地到乙地的铁路路程约为615千米,高铁速度为300千米/小时,直达;动车速度为200千米/小时,行驶180千米后,中途要停靠徐州10分钟,若动车先出发半小时,两车与甲地之间的距离y(千米)与动车行驶时间x(小时)之间的函数图象为( )A、
A、60° B、35° C、25° D、15°10. 从甲地到乙地的铁路路程约为615千米,高铁速度为300千米/小时,直达;动车速度为200千米/小时,行驶180千米后,中途要停靠徐州10分钟,若动车先出发半小时,两车与甲地之间的距离y(千米)与动车行驶时间x(小时)之间的函数图象为( )A、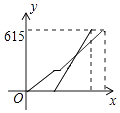 B、
B、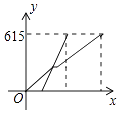 C、
C、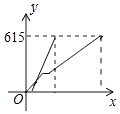 D、
D、
二、二.填空题(共6小题,满分24分,每小题4分)
-
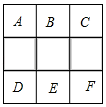
11. 不等式 <x的解是.12. 分解因式:ab﹣ab2=.13. 已知a2+a=1,则代数式3﹣a﹣a2的值为.14. 如图,现将方格内空白的小正方形(A,B,C,D,E,F)中任取2个涂黑,得到新图案.请用列表或画树状图的方法求新图案是轴对称图形的概率是.
 15. 如图2,小靓用边长为16的七巧板(如图1)拼成一幅装饰图,放入长方形ABCD内拼成一个“木马”形状(如图2),图中的三角形顶点E在边CD上,三角形的边AM、GF分别在边AD、BC上,则AB的长是.
15. 如图2,小靓用边长为16的七巧板(如图1)拼成一幅装饰图,放入长方形ABCD内拼成一个“木马”形状(如图2),图中的三角形顶点E在边CD上,三角形的边AM、GF分别在边AD、BC上,则AB的长是.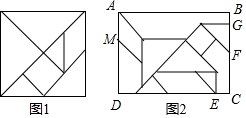 16. 港珠澳大桥是中国境内一座连接香港、珠海和澳门的桥隧工程,因其超大的建筑规模、空前的施工难度以及顶尖的建造技术而闻名世界.其主体工程青州航道桥是一座双塔双索面钢箱梁斜拉桥,两座索塔及索塔两侧的斜拉索对称分布,塔高AB为163米,大桥主跨BD的中点为E,记斜拉索与大桥主梁所夹锐角为α,那么用塔高和α的三角函数表示主跨BD的长为米.
16. 港珠澳大桥是中国境内一座连接香港、珠海和澳门的桥隧工程,因其超大的建筑规模、空前的施工难度以及顶尖的建造技术而闻名世界.其主体工程青州航道桥是一座双塔双索面钢箱梁斜拉桥,两座索塔及索塔两侧的斜拉索对称分布,塔高AB为163米,大桥主跨BD的中点为E,记斜拉索与大桥主梁所夹锐角为α,那么用塔高和α的三角函数表示主跨BD的长为米.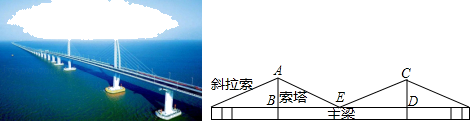
三、三.解答题(共8小题)
-
17. 计算: ×( )﹣2﹣|1﹣ |+3tan30°
18. 解方程组:19. 如图,在5×5的正方形网格,每个小正方形的边长都为1,线段AB的端点落在格点上,要求画一个四边形,所作的四边形为中心对称图形,同时满足下列要求: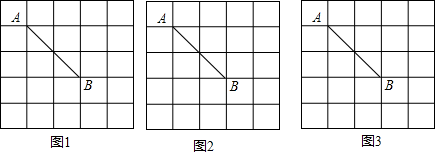 (1)、在图1中画出以AB为一边的四边形;(2)、分别在图2和图3中各画出一个以AB为一条对角线的四边形.20. 随着生活水平的日益提高,人们越来越喜欢过节,节日的仪式感日渐浓烈,某校举行了“母亲节暖心特别行动”,从中随机调查了部分同学的暖心行动,并将其分为A,B,C,D四种类型(分别对应送服务、送鲜花、送红包、送话语).现根据调查的数据绘制成如下的条形统计图和扇形统计图.
(1)、在图1中画出以AB为一边的四边形;(2)、分别在图2和图3中各画出一个以AB为一条对角线的四边形.20. 随着生活水平的日益提高,人们越来越喜欢过节,节日的仪式感日渐浓烈,某校举行了“母亲节暖心特别行动”,从中随机调查了部分同学的暖心行动,并将其分为A,B,C,D四种类型(分别对应送服务、送鲜花、送红包、送话语).现根据调查的数据绘制成如下的条形统计图和扇形统计图.请根据以上不完整的统计图提供的信息,解答下列问题:
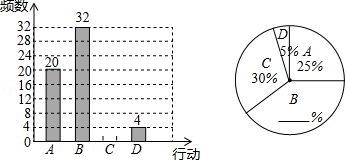 (1)、该校共抽查了多少名同学的暖心行动?(2)、求出扇形统计图中扇形B的圆心角度数?(3)、若该校共有2400名同学,请估计该校进行送鲜花行动的同学约有多少名?21. 如图,点O在△ABC的BC边上,⊙O经过点A、C,且与BC相交于点 D.点E是下半圆弧的中点,连接AE交BC于点F,已知AB=BF.
(1)、该校共抽查了多少名同学的暖心行动?(2)、求出扇形统计图中扇形B的圆心角度数?(3)、若该校共有2400名同学,请估计该校进行送鲜花行动的同学约有多少名?21. 如图,点O在△ABC的BC边上,⊙O经过点A、C,且与BC相交于点 D.点E是下半圆弧的中点,连接AE交BC于点F,已知AB=BF.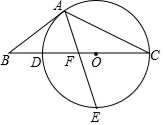 (1)、求证:AB是⊙O的切线;(2)、若OC=3,OF=1,求cosB的值.22. 如图所示,M、N、P在第二象限,横坐标分别是﹣4、﹣2、﹣1,双曲线y= 过M、N、P三点,且MN=NP.
(1)、求证:AB是⊙O的切线;(2)、若OC=3,OF=1,求cosB的值.22. 如图所示,M、N、P在第二象限,横坐标分别是﹣4、﹣2、﹣1,双曲线y= 过M、N、P三点,且MN=NP.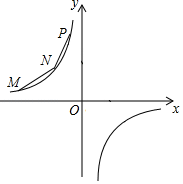 (1)、求双曲线的解析式;(2)、过P点的直线l交x轴于A,交y轴于B,且PA=4AB,且交y= 于另一点Q,求Q点坐标;(3)、以PN为边(顺时针方向)作正方形PNEF,平移正方形使N落在x轴上,点P、E对应的点P′、E'正好落在反比例函数y= 上,求F对应点F′的坐标.23. 如图,矩形ABCD中,AD=3,AB=4,点P是对角线AC上一动点(不与A,C重合),连结BP,作PE⊥PB,交射线DC于点E,以线段PE,PB为邻边作矩形BPEF.过点P作GH⊥CD,分别交AB、CD于点G、H.
(1)、求双曲线的解析式;(2)、过P点的直线l交x轴于A,交y轴于B,且PA=4AB,且交y= 于另一点Q,求Q点坐标;(3)、以PN为边(顺时针方向)作正方形PNEF,平移正方形使N落在x轴上,点P、E对应的点P′、E'正好落在反比例函数y= 上,求F对应点F′的坐标.23. 如图,矩形ABCD中,AD=3,AB=4,点P是对角线AC上一动点(不与A,C重合),连结BP,作PE⊥PB,交射线DC于点E,以线段PE,PB为邻边作矩形BPEF.过点P作GH⊥CD,分别交AB、CD于点G、H.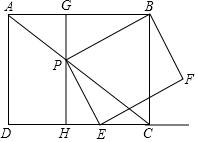 (1)、求证:△PGB∽△EHP;(2)、求 的值;(3)、求矩形BPEF的面积的最小值.24. 在平面直角坐标系中,抛物线y=﹣ax2+2ax+c与x轴相交于A(﹣1,0)、B两点(A点在B点左侧),与y轴相交于点C(0,3 ),点D是抛物线的顶点.
(1)、求证:△PGB∽△EHP;(2)、求 的值;(3)、求矩形BPEF的面积的最小值.24. 在平面直角坐标系中,抛物线y=﹣ax2+2ax+c与x轴相交于A(﹣1,0)、B两点(A点在B点左侧),与y轴相交于点C(0,3 ),点D是抛物线的顶点.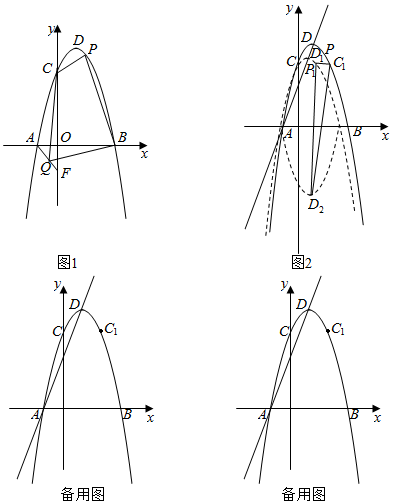 (1)、如图1,求抛物线的解析式;(2)、如图1,点F(0,b)在y轴上,连接AF,点Q是线段AF上的一个动点,P是第一象限抛物线上的一个动点,当b=﹣ 时,求四边形CQBP面积的最大值与点P的坐标;(3)、如图2,点C1与点C关于抛物线对称轴对称.将抛物线y沿直线AD平移,平移后的抛物线记为y1 , y1的顶点为D1 , 将抛物线y1沿x轴翻折,翻折后的抛物线记为y2 , y2的顶点为D2.在(2)的条件下,点P平移后的对应点为P1 , 在平移过程中,是否存在以P1D2为腰的等腰△C1P1D2 , 若存在请直接写出点D2的横坐标,若不存在请说明理由.
(1)、如图1,求抛物线的解析式;(2)、如图1,点F(0,b)在y轴上,连接AF,点Q是线段AF上的一个动点,P是第一象限抛物线上的一个动点,当b=﹣ 时,求四边形CQBP面积的最大值与点P的坐标;(3)、如图2,点C1与点C关于抛物线对称轴对称.将抛物线y沿直线AD平移,平移后的抛物线记为y1 , y1的顶点为D1 , 将抛物线y1沿x轴翻折,翻折后的抛物线记为y2 , y2的顶点为D2.在(2)的条件下,点P平移后的对应点为P1 , 在平移过程中,是否存在以P1D2为腰的等腰△C1P1D2 , 若存在请直接写出点D2的横坐标,若不存在请说明理由.