浙江省金华市金东区2020年数学中考一模试卷
试卷更新日期:2020-06-18 类型:中考模拟
一、仔细选一选(本大题有10小题,每小题3分,共30分。)
-
1. 下列四个几何体中,主视图与左视图相同的几何体有( )
 A、1个 B、2个 C、3个 D、4个2. 下列调查中,须用普查的是( )A、了解我区初三同学的视力情况 B、了解我区初三同学课外阅读的情况 C、了解我区初三同学今年4月12日回校报到时的校园健康“入学码”情况 D、了解我区初三同学疫情期间参加晨练的情况3. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
A、1个 B、2个 C、3个 D、4个2. 下列调查中,须用普查的是( )A、了解我区初三同学的视力情况 B、了解我区初三同学课外阅读的情况 C、了解我区初三同学今年4月12日回校报到时的校园健康“入学码”情况 D、了解我区初三同学疫情期间参加晨练的情况3. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 已知 则a+b等于( )A、 B、3 C、2 D、15. 如图是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为8cm,水面最深地方的高度为2cm,则该输水管的半径为( )
4. 已知 则a+b等于( )A、 B、3 C、2 D、15. 如图是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为8cm,水面最深地方的高度为2cm,则该输水管的半径为( )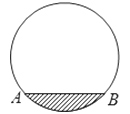 A、3cm B、4cm C、5cm D、6cm6. 下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )
A、3cm B、4cm C、5cm D、6cm6. 下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )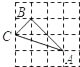 A、
A、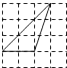 B、
B、 C、
C、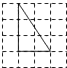 D、
D、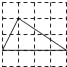 7. 分解因式 的结果是( )A、 B、 C、 D、8. 下列计算错误的是( )A、 B、 C、 D、9. 求1+2+22+23+…+22020的值,可令S=1+2+22+23+…+22020 , 则2S=2+22+23+24+…+22021 , 因此2S-S=22021-1.仿照以上推理,计算出1+2020+20202+20203+…+20202020的值为( )A、 B、 C、 D、10. 如图,在菱形纸片ABCD中,∠A=60°,将纸片折叠,点A,D分别落在点A',D'处,且A'D'经过点B,EF为折痕,当D'F⊥CD时, 的值为( )
7. 分解因式 的结果是( )A、 B、 C、 D、8. 下列计算错误的是( )A、 B、 C、 D、9. 求1+2+22+23+…+22020的值,可令S=1+2+22+23+…+22020 , 则2S=2+22+23+24+…+22021 , 因此2S-S=22021-1.仿照以上推理,计算出1+2020+20202+20203+…+20202020的值为( )A、 B、 C、 D、10. 如图,在菱形纸片ABCD中,∠A=60°,将纸片折叠,点A,D分别落在点A',D'处,且A'D'经过点B,EF为折痕,当D'F⊥CD时, 的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题有6小题,每小题4分,共24分)
-
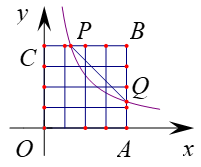
11. 已知∠α的补角是130°,则∠α的度数为.12. 太阳的半径为696000千米,把这个数据696000用科学记数法表示为.13. 从2,-2,-1这三数中任取两个不同数作为点坐标,则该点在第二象限的概率为.14. 已知y=x-1,则 的值为.15. 已知平面直角坐标系xOy,正方形OABC,点B(4,4),过边BC上动点P(不含端点C)的反比例函数 的图象交AB边于Q点,连结PQ,若把横、纵坐标均为整数的点叫做好点,则反比例函数图象与线段PQ围成的图形(含边界)中好点个数为三个时,k的取值范围为.
 16. 已知如图1,圆柱体铅笔插入卷笔刀充分卷削,得到底面直径BC为2的圆锥,∠BAC=30°. 底面边长为1的正六棱柱铅笔插入卷削,得到如图2所示铅笔和锯齿状木屑(木屑厚度忽略不计),木屑锯齿齿锋点G相邻凹陷最低点为H,则AG= , GH=.
16. 已知如图1,圆柱体铅笔插入卷笔刀充分卷削,得到底面直径BC为2的圆锥,∠BAC=30°. 底面边长为1的正六棱柱铅笔插入卷削,得到如图2所示铅笔和锯齿状木屑(木屑厚度忽略不计),木屑锯齿齿锋点G相邻凹陷最低点为H,则AG= , GH=.
三、解答题(本题有8小题,共66分。)
-
17. 计算: .18. 如图,E,F是四边形ABCD的对角线BD上的两点,AE∥CF,AE=CF,BE=DF.
求证:ΔADE≌ΔCBF.
 19. 一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,沿同一条道路匀速行驶.设行驶时间为t小时,两车之间的距离为s千米,图中折线A-B-C-D表示s与t之间的函数关系.
19. 一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,沿同一条道路匀速行驶.设行驶时间为t小时,两车之间的距离为s千米,图中折线A-B-C-D表示s与t之间的函数关系. (1)、求快车速度.(2)、当快车到达乙地时,慢车还要多少时间才能到达甲地。20. 某市教育局为了了解线上教学对视力影响,对参加2020年中考的50000名初中毕业生回校后立即进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:
(1)、求快车速度.(2)、当快车到达乙地时,慢车还要多少时间才能到达甲地。20. 某市教育局为了了解线上教学对视力影响,对参加2020年中考的50000名初中毕业生回校后立即进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题: (1)、在频数分布表中,a的值为 , b的值为 , 并将频数分布直方图补充完整.(2)、甲同学说“我的视力情况是此次抽样调查所得数据的中位数”,问甲同学的视力情况应在什么范围内?(3)、若视力在4.9以上(含4.9)均属正常,求视力正常的人数占被统计人数的百分比,并根据上述信息估计全市初中毕业生中视力正常的学生人数.21. 如图,AB为半圆O的直径,AC是⊙O的一条弦,D为 的中点,作DE⊥AC于点E,交AB的延长线于点F,连结AD.
(1)、在频数分布表中,a的值为 , b的值为 , 并将频数分布直方图补充完整.(2)、甲同学说“我的视力情况是此次抽样调查所得数据的中位数”,问甲同学的视力情况应在什么范围内?(3)、若视力在4.9以上(含4.9)均属正常,求视力正常的人数占被统计人数的百分比,并根据上述信息估计全市初中毕业生中视力正常的学生人数.21. 如图,AB为半圆O的直径,AC是⊙O的一条弦,D为 的中点,作DE⊥AC于点E,交AB的延长线于点F,连结AD. (1)、求证:EF为半圆O的切线.(2)、若AO=BF=2,求阴影区域的面积.22. 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC和△DEF(顶点为网格线的交点)以及格点P.
(1)、求证:EF为半圆O的切线.(2)、若AO=BF=2,求阴影区域的面积.22. 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC和△DEF(顶点为网格线的交点)以及格点P. (1)、①将△ABC向右平移五个单位长度,再向上平移一个单位长度,画出平移后的三角形.
(1)、①将△ABC向右平移五个单位长度,再向上平移一个单位长度,画出平移后的三角形.
②画出△DEF关于点P的中心对称三角形.(2)、求∠A+∠F的度数.23. 已知抛物线 , , ,…, (n为正整数),点A(0,1).

 (1)、如图1,过点A作y轴垂线,分别交抛物线 , , ,…, 于点 , , ,
(1)、如图1,过点A作y轴垂线,分别交抛物线 , , ,…, 于点 , , ,, ( 和点A不重合).
①求 的长.
②求 的长.
(2)、如图2,点P从点A出发,沿y轴向上运动,过点P作y轴的垂线,交抛物线 于点 , ,交抛物线 于点 , ,交抛物线 于点 , ,……,交抛物线 于点 , ( 在第二象限).①求 的值.
②求 的值.
(3)、过x轴上的点Q(原点除外),作x轴的垂线分别交抛物线 , , ,…, 于点 , , ,……, ,是否存在线段 (i,j为正整数),使 ,若存在,求出i + j的最小值;若不存在,说明理由.24. 如图,在等腰Rt△ABC中,∠ACB=90°,AB= . 点D,E分别在边AB,AC上,将线段ED绕点E按逆时针方向旋转90°得到EF,连结BF,BF的中点为G. (1)、当点E与点C重合时.
(1)、当点E与点C重合时.①如图1,若AD=BD,求BF的长.
②当点D从点A运动到点B时,求点G的运动路径长.
(2)、当AE=3,点G在△DEF一边所在直线上时,求AD的长.