辽宁省沈阳市沈北新区2020年数学中考一模试卷
试卷更新日期:2020-06-18 类型:中考模拟
一、选择题
-
1. 下列各数中最大的数是( )A、5 B、 C、π D、-82. 随着“一带一路”建设的不断发展,我国已与多个国家建立了经贸合作关系,去年中哈铁路(中国至哈萨克斯坦)运输量达8200000吨,将8200000用科学记数法表示为( )A、 B、 C、 D、3. 如图是某几何体的三视图,该几何体是( )
 A、三棱柱 B、三棱锥 C、圆锥 D、圆柱4. 不等式x+1≥2的解集在数轴上表示正确的是( )A、
A、三棱柱 B、三棱锥 C、圆锥 D、圆柱4. 不等式x+1≥2的解集在数轴上表示正确的是( )A、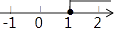 B、
B、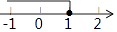 C、
C、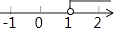 D、
D、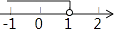 5. 下列计算正确的是( )
5. 下列计算正确的是( )
A、x4+x4=2x8 B、x3·x2=x6 C、(x2y)3=x6y3 D、(x-y)(y-x)=x2-y26. 点P(4,3)关于y轴的对称点所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 已知点A(﹣2,y1),B(﹣4,y2)都在反比例函数y= (k>0)的图象上,则y1 , y2的大小关系( )A、y1>y2 B、y1<y2 C、y1=y2 D、无法确定8. 如图,分别过矩形ABCD的顶点A,D作直线l1、l2 , 使l1∥l2 , l2与边BC交于点P,若∠1=38°,则∠BPD为( )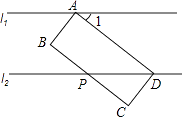 A、162° B、152° C、142° D、128°9. 某同学5次数学小测验的成绩分别为(单位:分):90,85,90,95,100,则该同学这5次成绩的众数是( )A、90 分 B、85 分 C、95 分 D、100 分10. 已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论正确的是( )
A、162° B、152° C、142° D、128°9. 某同学5次数学小测验的成绩分别为(单位:分):90,85,90,95,100,则该同学这5次成绩的众数是( )A、90 分 B、85 分 C、95 分 D、100 分10. 已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论正确的是( ) A、当x<2时,y随x增大而增大 B、a-b+c<0 C、拋物线过点(-4,0) D、4a+b=0
A、当x<2时,y随x增大而增大 B、a-b+c<0 C、拋物线过点(-4,0) D、4a+b=0二、填空题
-
11. 分解因式:x4﹣2x2y2+y4=.12. 如图,每个小正方形边长为1,则△ABC边AC上的高BD的长为.
 13. 如图,正方形ABCD中,点E为对角线AC上一点,且AE=AB,则∠BEA的度数是度.
13. 如图,正方形ABCD中,点E为对角线AC上一点,且AE=AB,则∠BEA的度数是度.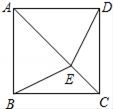 14. 口袋内装有一些除颜色外完全相同的红球、白球和黑球,从中摸出一球,摸出红球的概率是0.2,摸出白球的概率是0.5,那么摸出黑球的概率是 .
14. 口袋内装有一些除颜色外完全相同的红球、白球和黑球,从中摸出一球,摸出红球的概率是0.2,摸出白球的概率是0.5,那么摸出黑球的概率是 .
15. 如图:AB是⊙O的直径,C是⊙O上的一点,∠BAC的平分线交⊙O于D,若∠ABC = 400 , 则∠ABD = °. 16. 如图,在矩形ABCD中,AB=4,BC=6,将△ABE沿着AE折叠至△AB'E,若BE=CE,连接B'C,则B′C的长为.
16. 如图,在矩形ABCD中,AB=4,BC=6,将△ABE沿着AE折叠至△AB'E,若BE=CE,连接B'C,则B′C的长为.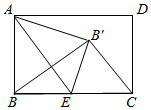
三、解答题
-
17. (π﹣3.14)0+|tan60°﹣3|﹣( )﹣2+ .18. 对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境.为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的A,B,C,D四个小区进行检查,并且每个小区不重复检查.(1)、甲组抽到A小区的概率是多少(2)、请用列表或画树状图的方法求甲组抽到A小区,同时乙组抽到C小区的概率.19. 某中学为了提高学生的综合素质,成立了以下社团A:机器人,B:围棋,C:羽毛球,D:电影配音.每人只能加入一个社团.为了解学生参加社团的情况,从参加社团的学生中随机抽取了部分学生进行调查,并将调查结果绘制成如图两幅不完整的统计图,其中图(1)中A所占扇形的圆心角为36°.
根据以上信息,解答下列问题:
 (1)、这次被调查的学生共有人;(2)、请你将条形统计图补充完整;(3)、若该校共有1000学生加入了社团,请你估计这1000名学生中有多少人参加了羽毛球社团.20. 如图,已知点E、F在四边形ABCD的对角线延长线上,AE=CF,DE∥BF,∠1=∠2.
(1)、这次被调查的学生共有人;(2)、请你将条形统计图补充完整;(3)、若该校共有1000学生加入了社团,请你估计这1000名学生中有多少人参加了羽毛球社团.20. 如图,已知点E、F在四边形ABCD的对角线延长线上,AE=CF,DE∥BF,∠1=∠2. (1)、求证:△AED≌△CFB;(2)、若AD⊥CD,四边形ABCD是什么特殊四边形?请说明理由.21. 九年级(1)班学生周末从学校出发到某实践基地,实践基地距学校150千米,一部分学生乘慢车先行,出发30分钟后,另一部分学生乘快车前往,结果他们同时到达实践基地.已知快车的速度是慢车速度的1.2倍.求慢车与快车的速度各是多少?22. 如图,在⊙O中,点D是⊙O上的一点,点C是直径AB延长线上一点,连接BD,CD,且∠A=∠BDC.
(1)、求证:△AED≌△CFB;(2)、若AD⊥CD,四边形ABCD是什么特殊四边形?请说明理由.21. 九年级(1)班学生周末从学校出发到某实践基地,实践基地距学校150千米,一部分学生乘慢车先行,出发30分钟后,另一部分学生乘快车前往,结果他们同时到达实践基地.已知快车的速度是慢车速度的1.2倍.求慢车与快车的速度各是多少?22. 如图,在⊙O中,点D是⊙O上的一点,点C是直径AB延长线上一点,连接BD,CD,且∠A=∠BDC. (1)、求证:直线CD是⊙O的切线;(2)、若CM平分∠ACD,且分别交AD,BD于点M,N,当DM=2时,求MN的长.23. 如图,平面直角坐标系中,直线y=﹣ x+ 与坐标轴交与点A、B.点C在x轴的负半轴上,且AB:AC=1:2.
(1)、求证:直线CD是⊙O的切线;(2)、若CM平分∠ACD,且分别交AD,BD于点M,N,当DM=2时,求MN的长.23. 如图,平面直角坐标系中,直线y=﹣ x+ 与坐标轴交与点A、B.点C在x轴的负半轴上,且AB:AC=1:2. (1)、求A、C两点的坐标;(2)、若点M从点C出发,以每秒1个单位的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,写出S关于t的函数关系式,并写出自变量的取值范围;(3)、点P是y轴上的点,在坐标平面内是否存在点Q,使以A、B、P、Q为顶点,且以AB为边的四边形是菱形,若存在,请直接写出点Q的坐标;若不存在,请说明理由.24. 如图
(1)、求A、C两点的坐标;(2)、若点M从点C出发,以每秒1个单位的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,写出S关于t的函数关系式,并写出自变量的取值范围;(3)、点P是y轴上的点,在坐标平面内是否存在点Q,使以A、B、P、Q为顶点,且以AB为边的四边形是菱形,若存在,请直接写出点Q的坐标;若不存在,请说明理由.24. 如图

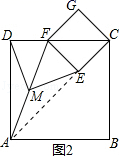
猜想与证明:
(1)、如图1,摆放矩形纸片ABCD与矩形纸片ECGF,使B、C、G三点在一条直线上,CE在边CD上,连接AF,若M为AF的中点,连接DM、ME,试猜想DM与ME的关系,并证明你的结论.(2)、若将”猜想与证明“中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为.(3)、如图2摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF的中点,试证明(1)中的结论仍然成立.25.已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
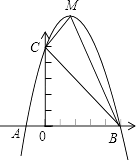 (1)、求抛物线的解析式;(2)、求△MCB的面积S△MCB .(3)、在坐标轴上,是否存在点N,满足△BCN为直角三角形?如存在,请直接写出所有满足条件的点N.
(1)、求抛物线的解析式;(2)、求△MCB的面积S△MCB .(3)、在坐标轴上,是否存在点N,满足△BCN为直角三角形?如存在,请直接写出所有满足条件的点N.