甘肃省临洮县2020年数学中考一模试卷
试卷更新日期:2020-06-18 类型:中考模拟
一、选择题
-
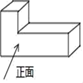
1. 9的算术平方根是( )A、 3 B、9 C、±3 D、±92. 如图所示的几何体左视图是( )
 A、
A、 B、
B、 C、
C、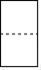 D、
D、 3. 在正数范围内定义一种运算☆,其规则为a☆b= ,根据这个规则x☆(x+1)= 的解为( )A、x= B、x=1 C、x=﹣ 或1 D、x= 或﹣14. 若一个多边形的内角和是1080度,则这个多边形的边数为( )A、6 B、7 C、8 D、105. 下列一元二次方程中,没有实数根的是( )A、 B、 C、 D、6. 在“朗读者”节目的影响下,某中学开展了“好书伴我成长”读书活动,为了解5月份八年级300名学生读书情况,随机调查了八年级50名学生读书的册数,统计数据如下表所示:
3. 在正数范围内定义一种运算☆,其规则为a☆b= ,根据这个规则x☆(x+1)= 的解为( )A、x= B、x=1 C、x=﹣ 或1 D、x= 或﹣14. 若一个多边形的内角和是1080度,则这个多边形的边数为( )A、6 B、7 C、8 D、105. 下列一元二次方程中,没有实数根的是( )A、 B、 C、 D、6. 在“朗读者”节目的影响下,某中学开展了“好书伴我成长”读书活动,为了解5月份八年级300名学生读书情况,随机调查了八年级50名学生读书的册数,统计数据如下表所示:册数
0
1
2
3
4
人数
4
12
16
17
1
关于这组数据,下列说法正确的是( )
A、中位数是2 B、众数是17 C、平均数是2 D、方差是27. 反比例函数y= (k>0)在第一象限内的图象如图,点M是图象上一点,MP垂直x轴于点P,如果△MOP的面积为1,那么k的值是( )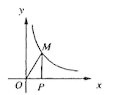 A、1 B、2 C、4 D、8. 如图,⊙C过原点,且与两坐标轴分别交于点A,点B,点A的坐标为(0,3),M是第三象限内 上一点,∠BMO=120°,则⊙C的半径长为( )
A、1 B、2 C、4 D、8. 如图,⊙C过原点,且与两坐标轴分别交于点A,点B,点A的坐标为(0,3),M是第三象限内 上一点,∠BMO=120°,则⊙C的半径长为( )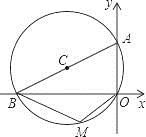 A、6 B、5 C、3 D、9. 甲车行驶30千米与乙车行驶40千米所用时间相同,已知乙车每小时比甲车多行驶15千米,设甲车的速度为x千米/小时,依据题意列方程正确的是( )A、 B、 C、 D、10. 如图抛物线y=ax2+bx+c的对称轴为直线x=1,且过点(3,0),下列结论:①abc>0;②a﹣b+c<0;③2a+b>0;④b2﹣4ac>0;正确的有( )个.
A、6 B、5 C、3 D、9. 甲车行驶30千米与乙车行驶40千米所用时间相同,已知乙车每小时比甲车多行驶15千米,设甲车的速度为x千米/小时,依据题意列方程正确的是( )A、 B、 C、 D、10. 如图抛物线y=ax2+bx+c的对称轴为直线x=1,且过点(3,0),下列结论:①abc>0;②a﹣b+c<0;③2a+b>0;④b2﹣4ac>0;正确的有( )个.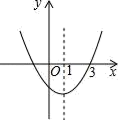 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 分解因式:a3﹣a= .12. 若3x=4,3y=6,则3x﹣2y的值是.13. 不等式组 的整数解是x= .
14. 在函数 的图象上有三个点(﹣2,y1),(﹣1,y2),( ,y3),则y1 , y2 , y3的大小关系为.15. 如图,已知:△ABC中,DE∥BC,AD=3,DB=6,AE=2,则EC=.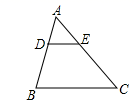 16. 如图,在扇形AOB中,∠AOB=90°,正方形CDEF的顶点C在弧AB上,使得弧BC=2弧AC,点D在OB上,点E在OB的延长线上,当CF=2 时,阴影部分的面积为.
16. 如图,在扇形AOB中,∠AOB=90°,正方形CDEF的顶点C在弧AB上,使得弧BC=2弧AC,点D在OB上,点E在OB的延长线上,当CF=2 时,阴影部分的面积为.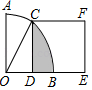 17. 如图,在矩形ABCD中,AB=2,BC=4,把矩形折叠,使点D与点B重合,点C落在点E处,则折痕FG的长为.
17. 如图,在矩形ABCD中,AB=2,BC=4,把矩形折叠,使点D与点B重合,点C落在点E处,则折痕FG的长为.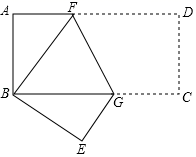 18. 如图所示,图①是一个三角形,分别连接三边中点得图②,再分别连接图②中的小三角形三边中点,得图③……按此方法继续下去.
18. 如图所示,图①是一个三角形,分别连接三边中点得图②,再分别连接图②中的小三角形三边中点,得图③……按此方法继续下去.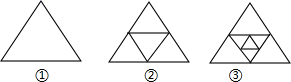
在第 个图形中有个三角形(用含 的式子表示)
三、解答题
-
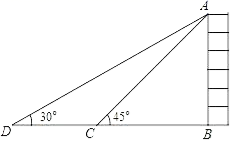
19. 计算:20. 先化简,再求值: ,其中 .21. 某校为迎接县中学生篮球比赛,计划购买A、B两种篮球共20个供学生训练使用.若购买A种篮球6个,则购买两种篮球共需费用720元;若购买A种篮球12个,则购实两种篮球共需费用840元.(1)、A、B两种篮球共需单价各多少元?(2)、设购买A种篮球x个且A种篮球不少于8个,所需费用为y元,试确定y与x的关系式.22. 如图所示,初三数学兴趣小组同学为了测量垂直于水平地面的一座大厦AB的高度,一测量人员在大厦附近C处,测得建筑物顶端A处的仰角大小为45°,随后沿直线BC向前走了60米后到达D处,在D处测得A处的仰角大小为30°,则大厦AB的高度约为多少米?(注:不计测量人员的身高,结果按四舍五入保留整数,参考数据: ≈1.41, ≈1.73)
 23. 有两个口袋,A口袋中装有两个分别标有数字2 、3的小球;B口袋中装有三个分别标有数字-1,4,-5的小球.小明先从A口袋中随机取出—个小球,用m表示所取球上的数字,再从B口袋中随机取出两个小球,用n表示所取球上的数字之和.(1)、用树状图法表示小明所取出的三个小球的所有可能结果;(2)、求 的值是整数的概率.24. 甘肃省注重建设“书香校园”.为了了解学生们的课外阅读情况,张老师调查了全班50名学生在一周内的课外阅读时间,并将统计的时间(单位:小时)分成5组:A.0.5≤x<1;B.1≤x<1.5;C.1.5≤x<2;D.2≤x<2.5;E.2.5≤x<3;并制成两幅不完整的统计图表如下:
23. 有两个口袋,A口袋中装有两个分别标有数字2 、3的小球;B口袋中装有三个分别标有数字-1,4,-5的小球.小明先从A口袋中随机取出—个小球,用m表示所取球上的数字,再从B口袋中随机取出两个小球,用n表示所取球上的数字之和.(1)、用树状图法表示小明所取出的三个小球的所有可能结果;(2)、求 的值是整数的概率.24. 甘肃省注重建设“书香校园”.为了了解学生们的课外阅读情况,张老师调查了全班50名学生在一周内的课外阅读时间,并将统计的时间(单位:小时)分成5组:A.0.5≤x<1;B.1≤x<1.5;C.1.5≤x<2;D.2≤x<2.5;E.2.5≤x<3;并制成两幅不完整的统计图表如下:组别
人数
占总数的百分比
A
3
B
C
40%
D
9
E
1
总计
50
100%
请根据图表中提供的信息,解答下列问题:
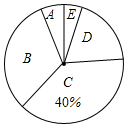 (1)、这次调查中学生课外阅读时间的中位数所在的组是;(2)、扇形统计图中,B组的圆心角为 ▲ , 并补全统计图表;(3)、请根据以上调查情况估计:全校1500名学生中有多少名学生每周阅读时间不低于2小时?25. 如图,直线y=kx+2与x轴,y轴分别交于点A(﹣1,0)和点B,与反比例函数y= 的图象在第一象限内交于点C(1,n).
(1)、这次调查中学生课外阅读时间的中位数所在的组是;(2)、扇形统计图中,B组的圆心角为 ▲ , 并补全统计图表;(3)、请根据以上调查情况估计:全校1500名学生中有多少名学生每周阅读时间不低于2小时?25. 如图,直线y=kx+2与x轴,y轴分别交于点A(﹣1,0)和点B,与反比例函数y= 的图象在第一象限内交于点C(1,n).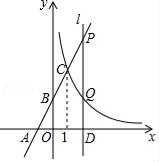 (1)、求一次函数y=kx+2与反比例函数y= 的表达式;(2)、过x轴上的点D(a,0)作平行于y轴的直线l(a>1),分别与直线y=kx+2和双曲线y= 交于P、Q两点,且PQ=2QD,求点D的坐标.26. 已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)、求一次函数y=kx+2与反比例函数y= 的表达式;(2)、过x轴上的点D(a,0)作平行于y轴的直线l(a>1),分别与直线y=kx+2和双曲线y= 交于P、Q两点,且PQ=2QD,求点D的坐标.26. 已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.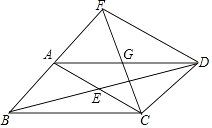 (1)、求证:AB=AF;(2)、若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.
(1)、求证:AB=AF;(2)、若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.
27. 如图,AB为⊙O直径,C、D为⊙O上的点,∠ACD=2∠A,CE⊥DB交DB的延长线于点E. (1)、求证:直线CE与⊙O相切;(2)、若AC=8,AB=10,求CE的长.28. 如图抛物线y=x2+bx+c(c<0)与x轴交于A、B两点,(点A在点B的左侧),与y轴交于点C,顶点为D,且OB=OC=3,点E为线段BD上的一个动点,EF⊥x轴于F.
(1)、求证:直线CE与⊙O相切;(2)、若AC=8,AB=10,求CE的长.28. 如图抛物线y=x2+bx+c(c<0)与x轴交于A、B两点,(点A在点B的左侧),与y轴交于点C,顶点为D,且OB=OC=3,点E为线段BD上的一个动点,EF⊥x轴于F.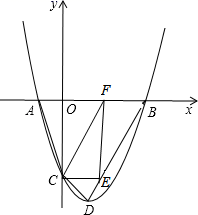 (1)、求抛物线的解析式;(2)、是否存在点E,使△ECF为直角三角形?若存在,求点E的坐标;不存在,请说明理由;(3)、连接AC、BC,若点P是抛物线上的一个动点,当P运动到什么位置时,∠PCB=∠ACO,请直接写出点P的坐标.
(1)、求抛物线的解析式;(2)、是否存在点E,使△ECF为直角三角形?若存在,求点E的坐标;不存在,请说明理由;(3)、连接AC、BC,若点P是抛物线上的一个动点,当P运动到什么位置时,∠PCB=∠ACO,请直接写出点P的坐标.