江苏省无锡市锡北片2019-2020学年七年级下学期数学期中考试试卷
试卷更新日期:2020-06-18 类型:期中考试
一、选择题
-
1. 把图形(1)进行平移,得到的图形是( )
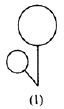 A、
A、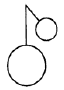 B、
B、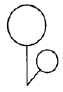 C、
C、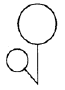 D、
D、 2. 下列等式从左到右的变形,属于因式分解的是( )A、 B、 C、 D、3. 已知某三角形的两边长是6和4,则此三角形的第三边长的取值可以是( )A、2 B、9 C、10 D、114. 下列计算正确的是( )A、 B、 C、 D、5. 如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=70°,则∠AED度数为( )
2. 下列等式从左到右的变形,属于因式分解的是( )A、 B、 C、 D、3. 已知某三角形的两边长是6和4,则此三角形的第三边长的取值可以是( )A、2 B、9 C、10 D、114. 下列计算正确的是( )A、 B、 C、 D、5. 如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=70°,则∠AED度数为( )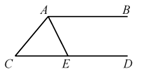 A、110° B、125° C、135° D、140°6. 若 ,则 等于( )A、 B、 C、 D、7. 下列说法中,正确的个数有( )
A、110° B、125° C、135° D、140°6. 若 ,则 等于( )A、 B、 C、 D、7. 下列说法中,正确的个数有( )①同位角相等; ②三角形的高相交于三角形的内部;③三角形的一个外角大于任意一个内角;④一个多边形的边数每增加一条,这个多边形的内角和就增加180°;⑤两个角的两边分别平行,则这两个角相等.
A、0个 B、1个 C、2个 D、3个8. 已知 ,则比较a、b、c、d的大小结果是( )A、 B、 C、 D、9. 将一副三角板如图摆放,∠OAB=∠OCD=90°,∠AOB=60°,∠COD=45°,OM平分∠AOD,ON平分∠COB,则∠MON的度数为( ) A、60° B、45° C、65.5° D、52.5°10. 如图,若平行四边形AFPE、BGPF、EPHD的面积分别为15、6、25,则阴影部分的面积是( )
A、60° B、45° C、65.5° D、52.5°10. 如图,若平行四边形AFPE、BGPF、EPHD的面积分别为15、6、25,则阴影部分的面积是( ) A、20 B、15.5 C、23 D、25
A、20 B、15.5 C、23 D、25二、填空题
-
11. 2019年末,新型冠状病毒引发的肺炎在我国爆发,被命名为2019-nCoV的新型冠状病毒直径最小约0.00000006厘米,用科学记数法表示为厘米.12. 若 是一个完全平方式,则m的值是.13. 若4x=2,4y=3,则14. 计算 的结果不含 的项,那么m=.15. 将长方形ABCD折叠,折痕为EF,BC的对应边为 与CD交于点M,若∠ =50°,则∠BEF的度数为°.
 16. 计算: =.17. 如图所示,过正五边形 的顶点 作一条射线与其内角 的角平分线相交于点 ,且 ,则 度.
16. 计算: =.17. 如图所示,过正五边形 的顶点 作一条射线与其内角 的角平分线相交于点 ,且 ,则 度.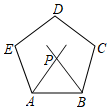 18. 无锡市旅游局为了亮化某景点,在两条笔直且互相平行的景观道MN、QP上分别放置A、B两盏激光灯,如图所示.A灯发出的光束自AM逆时针旋转至AN便立即回转;B灯发出的光束自BP逆时针旋转至BQ便立即回转,两灯不间断照射,A灯每秒转动30°,B灯每秒转动10°.B灯先转动2秒,A灯才开始转动.当B灯光束第一次到达BQ之前,两灯的光束互相平行时A灯旋转的时间是秒.
18. 无锡市旅游局为了亮化某景点,在两条笔直且互相平行的景观道MN、QP上分别放置A、B两盏激光灯,如图所示.A灯发出的光束自AM逆时针旋转至AN便立即回转;B灯发出的光束自BP逆时针旋转至BQ便立即回转,两灯不间断照射,A灯每秒转动30°,B灯每秒转动10°.B灯先转动2秒,A灯才开始转动.当B灯光束第一次到达BQ之前,两灯的光束互相平行时A灯旋转的时间是秒.
三、解答题
-
19. 计算:(1)、 ;(2)、 ;(3)、 ;(4)、 .20. 因式分解:(1)、 ;(2)、 ;(3)、 .21. 先化简,再求值:6x2-(2x+1)(3x-2)+(x+3)(x-3),其中22. 如图,在10×10的正方形网格中,每个小正方形的边长为1个单位长度.△ABC的顶点都在正方形网格的格点上,且通过两次平移(沿网格线方向作上下或左右平移)后得到△ ,点C的对应点是直线上的格点 .
 (1)、画出△ .(2)、若连接 、 ,则这两条线段之间的关系是.(3)、试在直线 上画出所有符合题意的格点P,使得由点 、 、 、P四点围成的四边形的面积为9.23. 如图,AD⊥BC,垂足为D,点E、F分别在线段AB、BC上,∠CAD=∠DEF,∠C+∠ADE=90°.
(1)、画出△ .(2)、若连接 、 ,则这两条线段之间的关系是.(3)、试在直线 上画出所有符合题意的格点P,使得由点 、 、 、P四点围成的四边形的面积为9.23. 如图,AD⊥BC,垂足为D,点E、F分别在线段AB、BC上,∠CAD=∠DEF,∠C+∠ADE=90°. (1)、求证:DE∥AC;(2)、判断EF与AD的位置关系,并证明你的猜想.24. 如图, 平分 , .
(1)、求证:DE∥AC;(2)、判断EF与AD的位置关系,并证明你的猜想.24. 如图, 平分 , . (1)、 与 相等吗?为什么?(2)、若 , ,求 的度数.25. 完全平方公式:(a±b)2=a2±2ab+b2适当的变形,可以解决很多的数学问题.
(1)、 与 相等吗?为什么?(2)、若 , ,求 的度数.25. 完全平方公式:(a±b)2=a2±2ab+b2适当的变形,可以解决很多的数学问题.例如:若a+b=3,ab=1,求a2+b2的值.
解:因为a+b=3,ab=1
所以(a+b)2=9,2ab=2
所以a2+b2+2ab=9,2ab=2
得a2+b2=7

根据上面的解题思路与方法,解决下列问题:
(1)、若(7﹣x)(x﹣4)=1,求(7﹣x)2+(x﹣4)2的值;(2)、如图,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设AB=5,两正方形的面积和S1+S2=17,求图中阴影部分面积.26. 在△ABC中,∠BAC=90°,点D是BC上一点,将△ABD沿AD翻折后得到△AED,边AE交射线BC于点F.(友情提醒:翻折前后的两个三角形的对应边相等,对应角相等.)

 (1)、如图①,当AE⊥BC时,求证:DE∥AC.(2)、若 ,∠BAD=x° .
(1)、如图①,当AE⊥BC时,求证:DE∥AC.(2)、若 ,∠BAD=x° .①如图②,当DE⊥BC时,求x的值;
②是否存在这样的x的值,使得△DEF中有两个角相等.若存在,并求x的值;若不存在,请说明理由.