陕西省延安市洛川县2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2020-06-18 类型：期末考试

进入出卷网下载

一、选择题

1. 下列调查中，最适合采用全面调查（普查）方式的是（）

A、对周末来信誉楼的顾客满意度的调查 B、对我校某班学生数学作业量的调查 C、对全国中学生手机使用时间情况的调查 D、环保部门对护城河水质情况的调查

查看试题解析
2. 下列运算中，正确的是（）

A、 $\sqrt{25^{2} - 1}$ ＝24 B、 $\sqrt{9 \frac{1}{4}}$ ＝3 $\frac{1}{2}$ C、 $\sqrt{81}$ ＝±9 D、－ $\sqrt{{(- \frac{1}{3})}^{2}}$ ＝－ $\frac{1}{3}$

查看试题解析
3. 不等式 $2 x + 2 \leq 6$ 的解集在数轴上表示正确的是 $($ 　　 $)$

A、 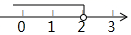B、 C、 D、

查看试题解析
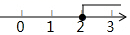4. 点A（m﹣4，1﹣2m）在第四象限，则m的取值范围是（）

A、m＞ $\frac{1}{2}$ B、m＞4 C、m＜4 D、 $\frac{1}{2}$ ＜m＜4

查看试题解析
5. 若二元一次方程组 ${\begin{array}{l} x + y = 3, \\ 3 x - 5 y = 4 \end{array}$ 的解为 ${\begin{array}{l} x = a, \\ y = b, \end{array}$ 则a-b的值为（）

A、1 B、3 C、 $- \frac{1}{4}$ D、 $\frac{7}{4}$

查看试题解析
6. 如果三角形有两边长分别为2和3，那么周长可能是下列哪个数（）

A、6 B、8 C、10 D、12

查看试题解析
7. 如图，在△ABC中，AB=AC，∠A=40°，∠ABC与外角∠ACE的平分线相交于点D，则∠D=（）

A、20° B、25° C、30° D、35°

查看试题解析
8. 如图，在△ABC和△DEF中，AB=DE，∠B=∠DEF，添加下列哪一个条件无法证明△ABC≌△DEF（）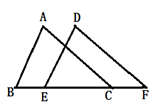

A、AC//DF B、∠A=∠D C、AC=DF D、BE=CF

查看试题解析
9. 一辆汽车从A地出发，向东行驶，途中要经过十字路口B，在规定的某一段时间内，若车速为每小时60千米，就能驶过B处2千米；若每小时行驶50千米，就差3千米才能到达B处，设A、B间的距离为x千米，规定的时间为y小时，则可列出方程组是（）

A、 ${\begin{array}{l} 60 y - x = 2 \\ x = 3 - 50 y \end{array}$ B、 ${\begin{array}{l} 60 y - x = 2 \\ 50 y - x = 3 \end{array}$ C、 ${\begin{array}{l} 60 y = x + 2 \\ 50 y = x - 3 \end{array}$ D、 ${\begin{array}{l} 60 y = x - 2 \\ 50 y = x - 3 \end{array}$

查看试题解析
10. 在下列一组图形中，能全等的三角形是（）

A、（1）和（6） B、（2）和（4），（3）和（5） C、（3）和（5） D、（2）和（4）

查看试题解析
11. 如图，DE⊥AB于E，DF⊥AC于F，若BD=CD，BE=CF，则下列结论：①DE=DF；①AD平分∠BAC；③AE=AD；④AB+AC=2AE.其中正确的有（）.

A、1个 B、2个 C、3个 D、4个

查看试题解析
12. 将一组数 $\sqrt{3}$ ， $\sqrt{6}$ ，3， $\sqrt{12}$ ， $\sqrt{15}$ ，…， $\sqrt{90}$ ，按下面的方法进行排列：
$\sqrt{3}$ ，   $\sqrt{6}$ ，    3，    $\sqrt{12}$ ，   $\sqrt{15}$ ；

$\sqrt{18}$ ， $\sqrt{21}$ ， $\sqrt{24}$ ， $\sqrt{27}$ ，   $\sqrt{30}$ ；

… …

若 $\sqrt{12}$ 的位置记为（1，4）， $\sqrt{21}$ 的位置记为（2，2），则这组数中最大的有理数的位置记为（   ）

A、（5，2） B、（5，3） C、（6，2） D、（6，5）

查看试题解析

二、填空题

13. 一个正数 $x$ 的两个平方根分别为 $2 a - 1$ 和 $- a + 2$ ，则正数 $x =$ .

查看试题解析
14. 如图，将一个三角形中含60°的角剪去，得到一个四边形，则∠1+∠2=.

查看试题解析
15. 如图，在象棋盘上建立平面直角坐标系，使“马”位于点（2，2），“炮”位于点（-1，2），则“兵”位于点 .

查看试题解析
16. 已知∠AOB，以点O为圆心，适当的长为半径画弧，交OA于点M，交OB于点N；分别以点M，N为圆心，大于 $\frac{1}{2}$ MN的长为半径画弧，两弧在∠AOB的内部相交于点C；则射线OC为∠AOB的平分线.依据是

查看试题解析
17. 若关于x的不等式组 ${\begin{matrix} x - m < 0 \\ 7 - 2 x \leq 1 \end{matrix}$ 的整数解共有4个，则m的取值范围是．

查看试题解析
18. 如图，在△ABC中，AD、AE分别是边BC上的中线与高，AE＝4，△ABC的面积为12，则CD的长为．

查看试题解析
19. 已知一次函数y＝kx＋b，当x＝2时，y＝－1；当x＝－1时，y＝5，则k＝， b＝.

查看试题解析
20. 如图，△ABC中，∠C=90°，AC=10cm，BC=5cm，线段PQ=AB，点P、Q分别在AC和与AC垂直的射线AM上移动，当AP= 时，△ABC和△QPA全等.

查看试题解析

三、解答题

21.

(1)、计算下列各式的值
① $\sqrt{{(- 3)}^{2}} - \sqrt[3]{- 8} + \sqrt{2} (\sqrt{2} - \frac{1}{\sqrt{2}})$ ； ② $\sqrt[3]{0.125} - \sqrt{2 \frac{1}{4}} \times \sqrt{{(- \frac{1}{3})}^{2}} - | 1 - \sqrt{2} |$ .

(2)、实数 $a ， b$ 在数轴上的位置如图所示，化简 $\sqrt{a^{2}} - \sqrt{b^{2}} - | a - b |$

查看试题解析
22. 解下列方程(组)和不等式组，并在数轴上表示不等式组的解集

(1)、 ${(x - 1)}^{2} = 9$

(2)、 ${\begin{array}{l} 4 (x - y - 1) = 3 (1 - y) - 2 \\ \frac{x}{2} + \frac{y}{3} = 2 \end{array}$

(3)、 ${\begin{array}{l} x - 3 (x - 2) \geq 4 \\ \frac{2 x - 1}{5} > \frac{x + 1}{2} - 1 \end{array}$

查看试题解析

23. “绿水青山就是金山银山”，为保护生态环境，某地准备开荒种树，两次参加活动的人数及开支如下表：

	开荒（人）	种树（人）	总支出（元）
第一次	15	9	57000
第二次	10	16	68000

(1)、若两次开荒种树活动的人均支出费用一样，求开荒和种树的人均支出费用各是多少？

(2)、在人均支出费用不变的情况下，为节约开支，施工单位准备抽调40人参加此活动，要使得总支出不超过102 000元，且开荒人数小于种树人数，则有哪几种分配人员方案？

查看试题解析

24. 如图，在△ABC中，∠ACB=90°，CD是AB边上的高，AB=13cm，BC=12cm，AC=5cm.

(1)、求△ABC的面积；

(2)、求CD的长；

(3)、作出△ABC的边AC上的中线BE，并求出△ABE的面积；

(4)、作出△BCD的边BC上的高DF，当BD= $m$ 时，试求出DF的长（用 $m$ 表示）.

查看试题解析
25. 某社区组织“献爱心手拉手”捐款活动.对社区部分捐款户数进行调查和分组统计后，将数据整理成如图所示的统计图和统计表（图中信息不完整）.已知A、B两组捐款户数的比为1：5.请结合以上信息解答下列问题.捐款户数分组统计表

(1)、本次调查了户；

(2)、补全“捐款户数分组统计表”和“捐款户数分组统计图1”；

(3)、若该社区有2000户住户，请根据以上信息，估计全社区捐款不少于150元的户数.

查看试题解析
26. 如图，在△ABC中，点D在线段BC上，∠1＝∠2，AE＝AC.

(1)、在不添加任何字母的情况下，请再补充一个条件，使得△ABC≌△ADE，你补充的条件是（至少写出两个可行的条件）；

(2)、请你从所给条件中选一个，使△ABC≌△ADE，并证明.

查看试题解析
27. 已知∠ABC=90°，D是直线AB边上的点，AD=BC

(1)、如图1，点D在线段AB上，过点A作AF⊥AB，且AF=BD，连接DC、DF、CF，试判断△CDF的形状并说明理由；

(2)、如图2，点D在线段AB的延长线上，点F在点A的左侧，其他条件不变，以上结论是否仍然成立？请说明理由.

查看试题解析