陕西省咸阳市永寿县2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期：2020-06-18 类型：期末考试
一、选择题
-
1. 下列图形中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 原子的一般直径是0.00000001cm，这个数据可以用科学记数法表示为（ ）A、1×10﹣8 B、1﹣8 C、1×108 D、183. 下列事件中，属于随机事件的是（ ）A、抛出的篮球往下落 B、在只有白球的袋子里摸出一个红球 C、购买 张彩票，中一等奖 D、地球绕太阳公转4. 若三角形的三边长分别为3，x，5，则x的值可以是（ ）A、2 B、5 C、8 D、115. 如图，已知AB∥CD，BC平分∠ABE，∠C=32°，则∠BED的度数是（ ）
A、32° B、16° C、49° D、64°6. 下列运算中，正确的是（ ）A、a2+a2=2a4 B、（a-b）2=a2-b2 C、（-x6）•（-x）2=x8 D、（-2a2b）3÷4a5=-2ab37. 正方形地板由9块边长均相等的小正方形组成，米粒随机地撒在如图所示的正方形地板上，那么米粒最终停留在黑色区城的概率是（ ）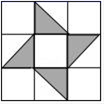
A、 B、 C、 D、8. 某同学带100元钱去买书，已知每册定价8.2元，买书后余下的钱y元和买的册数x之间的函数关系式是（ ）A、y=8.2x B、y=100-8.2x C、y=8.2x-100 D、y=100+8.2x9. 如图，已知AB⊥BC于B，CD⊥BC于C，BC=13，AB=5，且E为BC上一点，∠AED=90°，AE=DE，则BE=（ ）
A、13 B、8 C、6 D、510. 小明出校门后先加速行驶一段距离，然后以大小不变的速度行驶，在距家门不远的地方开始减速，最后停下，下面可以近似地刻画出以上情况的是 （ ）.A、
B、
C、
D、
二、填空题
-
11. 直角三角形中,一个锐角等于另一个锐角的2倍,则较小的锐角是.12. 如图， ，请你添加一个条件，使 ≌ ，你添加的条件是 写出一种情况即可 .
13. 已知x+y=5，xy=3，则x2+y2的值是 .14. 如图，△ABC中，AB=14，AC=12，沿过B点的直线折叠这个三角形，使点A落在BC边上的点E处，△CDE的周长为15，则BC长为.
三、解答题
-
15. 计算：(1)、1102-109×111(2)、（-2）2+30-（- ）-116. 先化简，再求值： ，其中 ， .17. 已知：如图，AD是△ABC的平分线，点E在BC上，点G在CA的延长线上，EG交AB于点F，且∠AFG＝∠G.
求证：GE∥AD.
18. 如图，在某住房小区的建设中，为了提高业主的直居环境，小区准备在一个长为（4a+3b）米，宽为（2a+3b）米的长方形草坪上修建两条宽为b米的通道.问剩余草坪的面积是多少平方米？
19. 小华在做关于弹簧的试验过程中，把一根弹簧的上端固定，在其下端悬挂物体，验证所挂物体重量与弹簧长度的关系，记录数据如表：所挂物体质量（千克）
0
1
2
3
4
5
弹簧长度（厘米）
12
15
18
21
24
27
据此回答下列问题：
(1)、上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？(2)、当所挂物体质量为5千克时，弹簧为多长？不挂重物时呢？(3)、当所挂重物为7千克（在允许范围内）时，你能说出此时的弹簧长度吗？20. 如图，已知网格上小正方形的边长为1个单位长度，点A、B、C在格点上.
(1)、画出△ABC关于直线l对称的△A'B'C'；(2)、求出△ABC的面积.21. 已知：如图，BC∥EF，点C，点F在AD上，AF＝DC，BC＝EF.求证：△ABC≌△DEF.
22. 在不透明的袋子中装有5个红球和8个黄球，每个球除颜色外都相同.(1)、从中任意摸出一个球，摸到球的可能性大.(2)、如果再放入若干个黄球并摇匀，随机摸出一个球是红球的概率是 ，请问放入了多少个黄球？23. 如图，两条射线AM∥BN，线段CD的两个端点C、D分别在射线BN、AM上，且∠A=∠BCD=108°.E是线段AD上一点（不与点A、D重合），且BD平分∠EBC.
(1)、求∠ABC的度数.(2)、请在图中找出与∠ABC相等的角，并说明理由.(3)、若平行移动CD，且AD＞CD，则∠ADB与∠AEB的度数之比是否随着CD位置的变化而发生变化？若变化，找出变化规律；若不变，求出这个比值.