陕西省城固县2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期：2020-06-18 类型：期末考试
一、选择题
-
1. 澳大利亚昆士兰大学的科学家在海底深处，发现了一种世界上最小的神秘生物，这种比细菌还要小的生物，身体非常小，计算单位要用0.000000001米.将数字0.000000001用科学记数法表示应为（ ）A、10×10-10 B、1×10-9 C、0.1×10-8 D、1×10-102. 低碳环保理念深入人心，共享单车已成为出行新方式 下列共享单车图标（不考虑外围方框），是轴对称图形的是A、
B、
C、
D、
3. 已知三角形两边长分别为3和8，则该三角形第三边的长可能是（ ）A、3 B、5 C、8 D、114. 如图，AB∥CD，EF⊥AB于E，EF交CD于F，已知∠2=20°，则∠1等于（ ）
A、30° B、50° C、70° D、45°5. 下列事件中，属于不确定事件的是（ ）A、抛掷一枚硬币，正面朝上 B、在空中抛掷石块，石块终将落下 C、小明的跑步速度是100米/秒 D、在一个标准大气压下，水到 就沸腾6. 某烤鸭店在确定烤鸭的烤制时间时，主要依据的是下表的数据：鸭的质量/千克
0.5
1
1.5
2
2.5
3
3.5
4
烤制时间/分
40
60
80
100
120
140
160
180
设鸭的质量为x千克，烤制时间为t分钟，估计当 时， 的值为（ ）
A、140 B、200 C、240 D、2607. 如图，ΔABC与ΔA’B’C’关于直线l对称，则∠B的度数为 （ ）
A、30° B、50° C、90° D、100°8. 如图，在 和 中， ，还需再添加两个条件才能使 ，则不能添加的一组条件是（ ）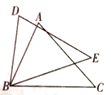
A、AC=DE，∠C=∠E B、BD=AB，AC=DE C、AB=DB，∠A=∠D D、∠C=∠E，∠A=∠D9. 某林业部门要考察某种幼树在一定条件下的移植成活率，下图是这种幼树在移植过程中成活情况的一组数据统计结果.下面三个推断：①当移植棵数是1500时，该幼树移植成活的棵数是1356，所以“移植成活”的概率是0.904；②随着移植棵数的增加，“移植成活”的频率总在0.880附近摆动，显示出一定的稳定性，可以估计这种幼树“移植成活”的概率是0.880；③若这种幼树“移植成活”的频率的平均值是0.875，则“移植成活”的概率是0.875.其中合理的是（ ）
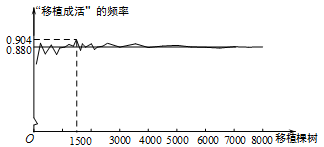A、①③ B、②③ C、① D、②10. 如图，AF∥CD，CB平分∠ACD，BD平分∠EBF，且BC⊥BD，下列结论：① BC平分∠ABE；② AC∥BE；③ ∠CBE+∠D＝90°；④ ∠DEB＝2∠ABC.其中正确结论的个数有（ ）
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 计算： .12. 如图，在△ABC中，AE是∠BAC的角平分线，AD是BC边上的高，且∠B=40°，∠C=60°，则∠EAD度数是.
13. 如图，△ABC中，∠C＝90°，AC＝BC，AD平分∠CAB交BC于D，DE⊥AB于点E，且AB＝6cm，则△DEB的周长是；
14. 二十四节气列入联合国教科文组织人类非物质文化遗产代表作名录.太阳运行的轨道是一个圆形，古人将之称作“黄道”，并把黄道分为24份，每15度就是一个节气，统称“二十四节气”.这一时间认知体系被誉为“中国的第五大发明”.如图，指针落在惊蛰、春分、清明区域的概率是.
三、解答题
-
15. 计算：[（a+2b）2-（a+2b）（a-2b）]÷4b.16. 如图，已知在 中，用直尺和圆规作 的平分线BD交AC于点D.（保留作图痕迹，不要求写作法）
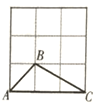
17. 如图，在 的正方形网格中，有格点 和 ，且 和 关于某条直线成轴对称，请在下面给出的图中，画出3个不同位置的 及其对称轴MN.
18. 一盘蚊香长105cm，点燃时每小时缩短10cm.(1)、请求出点燃后蚊香的长y（cm）与蚊香燃烧时间t（h）之间的关系式；(2)、该蚊香可点燃多长时间？19. 如图，操场上有两根旗杆间相距12m，小强同学从B点沿BA走向A，一定时间后他到达M点，此时他测得CM和DM的夹角为90°，且 ，已知旗杆AC的高为3m，求另一旗杆BD的高度.
20. 某批乒乓球的质量检验结果如下：
(1)、a= ， b=；(2)、在图中画出这批乒乓球“优等品”频率的折线统计图；
(3)、这批乒乓球“优等品”的概率的估计值是.21. 如图，已知 ， ， ， .AB与DE平行吗？为什么？
22. 用4个长7厘米、宽2厘米的长方形拼成一个大长方形(如图，左下角和右上角重叠)，大长方形的周长是多少厘米?图中阴影部分的面积是多少平方厘米?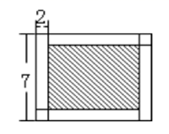
23. 甲袋里装有红球5个，白球2个和黑球12个，乙袋里装有红球20个，白球20个和黑球10个.(1)、如果你想取出1个黑球，选哪个袋子成功的机会大？请说明理由.(2)、某同学说“从乙袋取出10个红球后，乙袋中的红球个数仍比甲袋中红球个数多，所以此时想取出1个红球，选乙袋成功的机会大.”你认为此说法正确吗？为什么？24. 甲、乙两城市之间开通了动车组高速列车。已知每隔2h有一列速度相同的动车组列车从甲城开往乙城。如图，OA是第一列动车组列车离开甲城的路程s(km)与运行时间t(h)的函数图象，BC是一列从乙城开往甲城的普通快车距甲城的路程s(km)与运行时间t(h)的函数图象。请根据图中的信息，解答下列问题：
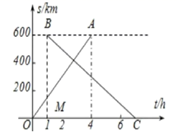(1)、从图象看，普通快车发车时间比第一列动车组列车发车时间1h(填“早”或“晚”)，点B的纵坐标600的实际意义是；(2)、请直接在图中画出第二列动车组列车离开甲城的路程s(km)与时间t(h)的函数图象；(3)、若普通快车的速度为100km/h，①求BC的表达式，并写出自变量的取值范围；
②第二列动车组列车出发多长时间后与普通快车相遇?
③请直接写出这列普通快车在行驶途中与迎面而来的相邻两列动车组列车相遇的时间间隔.
25. 如图①，△ABC是正三角形，△BDC是顶角∠BDC=120°的等腰三角形，以D为顶点作一个60°角，角两边分别交AB，AC边于M，N两点，连接MN.
(1)、探究：线段BM，MN，NC之间的关系，并加以证明.(2)、若点M是AB的延长线上的一点，N是CA的延长线上的点，其它条件不变，请你再探线段BM，MN，NC之间的关系，在图②中画出图形，并说明理由.