陕西省宝鸡市岐山县2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2020-06-18 类型:期末考试
一、选择题
-
1. 下面四个图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 花粉的质量很小,一粒某种植物花粉的质量约为 ,那么 用科学记数法表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 在一个不透明的布袋中,红球、黑球、白球共有若干个,除颜色外,形状、大小、质地等完全相同.小新从布袋中随机摸出一球,记下颜色后放回布袋中,摇匀后再随机摸出一球,记下颜色,……,如此大量摸球实验后,小新发出其中摸出红球的频率稳定于20%,摸出黑球的频率稳定于50%.对此实验,他总结出下列结论:①若进行大量摸球实验,摸出白球的频率应稳定于30%;②若从布袋中任意摸出一个球,该球是黑球的概率最大;③若再摸球100次,必有20次摸出的球是红球.其中说法正确的是( )A、①②③ B、①② C、①③ D、②③5. 如图,直线a∥b,∠2=35°,∠3=40°,则∠1的度数是( )
2. 花粉的质量很小,一粒某种植物花粉的质量约为 ,那么 用科学记数法表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 在一个不透明的布袋中,红球、黑球、白球共有若干个,除颜色外,形状、大小、质地等完全相同.小新从布袋中随机摸出一球,记下颜色后放回布袋中,摇匀后再随机摸出一球,记下颜色,……,如此大量摸球实验后,小新发出其中摸出红球的频率稳定于20%,摸出黑球的频率稳定于50%.对此实验,他总结出下列结论:①若进行大量摸球实验,摸出白球的频率应稳定于30%;②若从布袋中任意摸出一个球,该球是黑球的概率最大;③若再摸球100次,必有20次摸出的球是红球.其中说法正确的是( )A、①②③ B、①② C、①③ D、②③5. 如图,直线a∥b,∠2=35°,∠3=40°,则∠1的度数是( ) A、75° B、105° C、140° D、145°6. 如图,把一张长方形纸片 沿 折叠后, 与 相交于点G,点D、C分别落在点M、N的位置上,若 ,则 的度数为( )
A、75° B、105° C、140° D、145°6. 如图,把一张长方形纸片 沿 折叠后, 与 相交于点G,点D、C分别落在点M、N的位置上,若 ,则 的度数为( ) A、 B、 C、 D、7. 下列事件是随机事件的是( )A、随意掷一块质地均匀的骰子,掷出的点数是奇数 B、在一个标准大气压下,把水加热到100℃,水就会沸腾 C、有一名运动员奔跑的速度是80米/秒 D、在一个仅装着白球和黑球的袋中摸球,摸出红球8. 如图,点D,E分别在AC,AB上,BD与CE相交于点O,已知∠B=∠C,现添加下面的哪一个条件后,仍不能判定△ABD≌△ACE的是( )
A、 B、 C、 D、7. 下列事件是随机事件的是( )A、随意掷一块质地均匀的骰子,掷出的点数是奇数 B、在一个标准大气压下,把水加热到100℃,水就会沸腾 C、有一名运动员奔跑的速度是80米/秒 D、在一个仅装着白球和黑球的袋中摸球,摸出红球8. 如图,点D,E分别在AC,AB上,BD与CE相交于点O,已知∠B=∠C,现添加下面的哪一个条件后,仍不能判定△ABD≌△ACE的是( ) A、AD=AE B、AB=AC C、BD=CE D、∠ADB=∠AEC9. 下表是摄氏温度和华氏温度之间的对应表,则字母a的值是( )
A、AD=AE B、AB=AC C、BD=CE D、∠ADB=∠AEC9. 下表是摄氏温度和华氏温度之间的对应表,则字母a的值是( )华氏°F
23
32
41
a
59
摄氏℃
﹣5
0
5
10
15
A、45 B、50 C、53 D、6810. 如图, 是 的高, ,则 度数是( )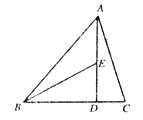 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 在一个不透明的袋子中有1个红球,2个绿球和3个白球,这些球除了颜色外完全一样,摇匀后,从袋子中任意摸出1个球,则摸到红球的概率是;你认为摸出颜色的球的可能性最大.12. 已知三角形的两边长分别为2和6,第三边的长是偶数,则此三角形的第三边长是.13. 如图,在△ABC中,∠A=36°,∠B=60°,EF∥BC,FG平分∠AFE,则∠AFG的度数为.
 14. 某剧院的观众席的座位为扇形,且按下列方式设置:
14. 某剧院的观众席的座位为扇形,且按下列方式设置:排数(x)
1
2
3
4
…
座位数(y)
50
53
56
59
…
写出座位数y与排数x之间的关系式
三、解答题
-
15. 计算:16. 王老师给学生出了一道题:
先化简,再求值: ,其中 , 。同学们看了题目后发表不同的看法.小张说:“条件 是多余的.”小李说:“不给这个条件,就不能求出结果,所以不多余.”
(1)、你认为他们谁说的有道理?为什么?(2)、若 的值等于此题计算的结果,试求 的值.17. 按要求作图.已知 ,点C是 上一点.
( 1 )过点C作直线 ;
( 2 )请在(1)中的直线 上求作一点 ,使点 到 , 的距离相等.(不写作法,保留作图痕迹)
18. 由16个相同的小正方形拼成的正方形网格,现将其中的两个小正方形涂黑(如图)。请你用两种不同的方法分别在上图中再将两个空白的小正方形涂黑,使它成为轴对称图形。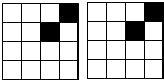 19. 如图,已知 ,直线 与 、 分别相交于点E、F, 与 的平分线相交于P,问: 吗?请说明理由.
19. 如图,已知 ,直线 与 、 分别相交于点E、F, 与 的平分线相交于P,问: 吗?请说明理由. 20. 乐乐家附近的商场为了吸引顾客,设立了一个可以自由转动的转盘, 为转盘直径,如图所示,并规定:顾客消费50元(含50元)以上,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准9折、8折、7折区域,则顾客就可以获得相应区域的优惠.
20. 乐乐家附近的商场为了吸引顾客,设立了一个可以自由转动的转盘, 为转盘直径,如图所示,并规定:顾客消费50元(含50元)以上,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准9折、8折、7折区域,则顾客就可以获得相应区域的优惠. (1)、某顾客在该商场消费40元,是否可以获得转动转盘的机会?(2)、某顾客在该商场正好消费66元,则他转动一次转盘,获得三种打折优惠的概率分别是多少?21. 小王周末骑电动车从家里出发去商场买东西,当他骑了一段路时,想起要买一本书,于是原路返回到刚经过的新华书店,买到书后继续前往商场,如图是他离家的距离(米)与时间(分钟)之间的关系示意图,请根据图中提供的信息回答下列问题:
(1)、某顾客在该商场消费40元,是否可以获得转动转盘的机会?(2)、某顾客在该商场正好消费66元,则他转动一次转盘,获得三种打折优惠的概率分别是多少?21. 小王周末骑电动车从家里出发去商场买东西,当他骑了一段路时,想起要买一本书,于是原路返回到刚经过的新华书店,买到书后继续前往商场,如图是他离家的距离(米)与时间(分钟)之间的关系示意图,请根据图中提供的信息回答下列问题: (1)、在此变化过程中,自变量是 , 因变量是.(2)、小王在新华书店停留了多长时间?(3)、买到书后,小王从新华书店到商场的骑车速度是多少?
(1)、在此变化过程中,自变量是 , 因变量是.(2)、小王在新华书店停留了多长时间?(3)、买到书后,小王从新华书店到商场的骑车速度是多少?