湖州市吴兴区2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2020-06-18 类型：期末考试

进入出卷网下载

一、选择题

1. 分式 $\frac{3}{x - 1}$ 有意义，则x的取值范围是（）

A、 $x \neq 1$ B、 $x \neq - 1$ C、 $x = 1$ D、 $x = - 1$

查看试题解析
2. 已知：如图，直线a，b被直线c所截，且a∥b.若∠1=70°，则∠2的度数是（）

A、 $130^{\circ}$ B、 $110^{\circ}$ C、 $80^{\circ}$ D、 $70^{\circ}$

查看试题解析
3. 下列计算结果正确的是（）

A、 $a^{3} \cdot a^{4} = a^{12}$ B、 $a^{5} \div a = a^{5}$ C、 ${(a b^{2})}^{3} = a b^{6}$ D、 ${(a^{3})}^{2} = a^{6}$

查看试题解析
4. 世界上最小的开花结果植物是澳大利亚的出水浮萍，它的果实像一粒微小的无花果，质量只有0.00000007g的，这个数值用科学记数法表示为（）

A、 $7 \times 10^{- 7}$ B、 $7 \times 10^{- 8}$ C、 $7 \times 10^{- 9}$ D、 $7 \times 10^{- 10}$

查看试题解析
5. 下列因式分解正确的是（　　）

A、a²+8ab+16b²=（a+4b）² B、a⁴﹣16=（a²+4）（a²﹣4） C、4a²+2ab+b²=（2a+b）² D、a²+2ab﹣b²=（a﹣b）²

查看试题解析
6. 端午节放假后，赵老师从七年级650名学生中随机抽查了其中50名学生的数学作业，发现有5名学生的作业不合格，下面判断正确的是（）

A、赵老师采用全面调查方式 B、个体是每名学生 C、样本容量是650 D、该七年级学生约有65名学生的作业不合格

查看试题解析
7. 若x²+2（2p﹣3）x+4是完全平方式，则p的值等于（）

A、 $\frac{5}{2}$ B、2 C、2或1 D、 $\frac{5}{2}$ 或 $\frac{1}{2}$

查看试题解析
8. 使得分式 $\frac{x}{x - 3} + \frac{2}{3 - x} - 2$ 的值为零时，x的值是（）

A、x=4 B、x=-4 C、x=4或x=-4 D、以上都不对

查看试题解析
9. 如图，直线 $l_{1}$ ， $l_{2}$ 表示一条河的两岸，且 $l_{1}$ ∥ $l_{2}$ 现要在这条河上建一座桥（桥与河的两岸相互垂直），使得从村庄A经桥过河到村庄B的路程最短，应该选择路线（）

A、 B、 C、 D、

查看试题解析
10. 已知关于x，y的方程组 ${\begin{matrix} x + 2 y = k + 2 \\ 2 x - 3 y = 3 k - 1 \end{matrix}$ 以下结论：①当x=1，y=2时，k=3；②当k=0，方程组的解也是y-x= $\frac{1}{7}$ 的解；③存在实数k，使x+y=0；④不论k取什么实数，x+9y的值始终不变，其中正确的是（）

A、②③ B、①②③ C、②③④ D、①②③④

查看试题解析

二、填空题

11. 因式分解：a²﹣3a=

查看试题解析
12. 对某班组织的一次考试成绩进行统计，已知80.5～90.5分这一组的频数是7，频率是0.2，那么该班级的人数是人．

查看试题解析
13. $3 x^{2} y \cdot$ = $18 x^{4} y^{3}$

查看试题解析
14. 若多项式x²-mx+n（m、n是常数）分解因式后，有一个因式是x-3，则3m-n的值为.

查看试题解析
15. 如图，将一条两边平行的纸带折叠，当∠2=80°，则∠1=.

查看试题解析
16. 六张形状大小完全相同的小长方形卡片，分两种不同形式不重叠的放在一个底面长为m，宽为n的长方形盒子底部（如图①、图②），盒子底面未被卡片覆盖的部分用阴影表示，设图①中阴影图形的周长为 $l_{1}$ ，图②中两个阴影部分图形的周长和为 $l_{2}$ 则用含m、n的代数式 $l_{1}$ = ， $l_{2}$ = ，若 $l_{1} = \frac{5}{3} l_{2}$ ，则m=（用含n的代数式表示）

查看试题解析

三、解答题

17. 计算：

(1)、 ${(- 1)}^{2019} + {(- 3)}^{- 1} + {(π - 0.1)}^{0}$

(2)、 $(2 a + 3) (3 - 2 a)$

查看试题解析
18.

(1)、解分式方程： $\frac{x}{x - 3} - 4 = \frac{3}{x - 3}$ ；

(2)、解二元一次方程组 ${\begin{array}{l} 2 x + y = 3 \\ 4 x - 3 y = 11 \end{array}$

查看试题解析
19. 化简，再求值： $\frac{a - 1}{a^{2} - 4} \div (1 - \frac{3}{a + 2})$ ，再从-2，-1，0，1，2选择一个你喜欢的数代入求值.

查看试题解析
20. 已知：如图，AB∥CD，DE∥BC.

(1)、判断∠B与∠D的数量关系，并说明理由.

(2)、若∠B=（105-2x）°，∠D=（5x+15）°，求∠B的度数.

查看试题解析
21. 某校5月组织了学生参加“学习强国”知识竞赛，从中抽取了部分学生成绩（满分为100分）进行统计，绘制如下不完整的频数直方图，若将频数直方图划分的五组从左至右依次记为A、B、C、D、E，绘制如下扇形统计图，请你根据图形提供的信息，解答下列问题：

(1)、频数分布直方图中，求A组的频数a，并补全频数直方图；

(2)、扇形统计图中，D部分所占的圆心角n=度；

(3)、若成绩在80分以上为优秀，全校共有2000名学生，估计成绩优秀的学生有多少名？

查看试题解析
22. 湖州奥体中心是一座多功能的体育场，目前体育场内有一块长80m，宽60m的长方形空地，体育局希望将其改建成花园小广场，设计方案如图，阴影区域是面积为192平方米的绿化区（四块相同的直角三角形），空白区域为活动区，且四周出口宽度一样.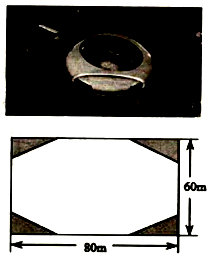

(1)、体育局先对四个绿化区域进行绿化，在完成工作量的 $\frac{1}{3}$ 后，施工方进行了技术改进，每天的绿化面积是原计划的两倍，结果提前四天完成四个绿化区域的改造，问原计划每天绿化多少平方米？

(2)、老师提出了一个问题：你能不能求出活动区的出口宽度是多少呢？

请你根据小丽的方法求出活动区的出口宽度，并把过程写下来.

查看试题解析
23. （阅读理解）
我们知道，1+2+3+…+n= $\frac{n (n + 1)}{2}$ ，那么1²+2²+3²+…+n²结果等于多少呢？

在图1所示三角形数阵中，第1行圆圈中的数为1，即1² ，第2行两个圆圈中数的和为2+2，即2² ， …；第n行n个圆圈中数的和为 $\underset{n 个 n}{\underset{�}{n + n + n + \dots + n}}$ ，即n² ，这样，该三角形数阵中共有 $\frac{n (n + 1)}{2}$ 个圆圈，所有圆圈中数的和为1²+2²+3²+…+n².

(1)、（规律探究）
将三角形数阵经两次旋转可得如图2所示的三角形数阵，观察这三个三角形数阵各行同一位置圆圈中的数（如第n﹣1行的第一个圆圈中的数分别为n﹣1，2，n），发现每个位置上三个圆圈中数的和均为，由此可得，这三个三角形数阵所有圆圈中数的总和为：3（1²+2²+3²+…+n²）= ，因此，1²+2²+3²+…+n²=.

(2)、（解决问题）
根据以上发现，计算： $\frac{1^{2} + 2^{2} + 3^{2} + \dots + 2017^{2}}{1 + 2 + 3 + \dots + 2017}$ 的结果为.

查看试题解析
24. 阅读下面材料：

(1)、小亮遇到这样问题：如图1，已知AB∥CD，EOF是直线AB、CD间的一条折线.判断∠O、∠BEO、∠DFO三个角之间的数量关系.小亮通过思考发现：过点O作OP∥AB，通过构造内错角，可使问题得到解决.
请回答：∠O、∠BEO、∠DFO三个角之间的数量关系是.

(2)、如图2，将△ABC沿BA方向平移到△DEF（B、D、E共线），∠B=50°，AC与DF相交于点G，GP、EP分别平分∠CGF、∠DEF相交于点P，求∠P的度数；

(3)、如图3，直线m∥n，点B、F在直线m上，点E、C在直线n上，连接FE并延长至点A，连接BA、BC和CA，做∠CBF和∠CEF的平分线交于点M，若∠ADC=α，则∠M=（直接用含α的式子表示）.

查看试题解析