广西壮族自治区北海市2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2020-06-18 类型:期末考试
一、选择题
-
1. 计算: =( )A、 B、 C、 D、2. 为丰富国民精神文化生活,提升文化素养,全国各地陆续开展全民阅读活动. 现在的图书馆不单是人们学习知识的地方,更是成为人们休闲的好去处. 下列图书馆标志的图形中不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 如图,已知 ,若 ,则 的度数为( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 如图,已知 ,若 ,则 的度数为( ) A、 B、 C、 D、5. 如图,下列条件中能判定 的是( )
A、 B、 C、 D、5. 如图,下列条件中能判定 的是( ) A、 B、 C、 D、6. 某校九年级(1)班全体学生2015年初中毕业体育考试的成绩统计如下表:
A、 B、 C、 D、6. 某校九年级(1)班全体学生2015年初中毕业体育考试的成绩统计如下表:成绩(分)
35
39
42
44
45
48
50
人数(人)
2
5
6
6
8
7
6
根据上表中的信息判断,下列结论中错误的是( )
A、该班一共有40名同学 B、该班学生这次考试成绩的众数是45分 C、该班学生这次考试成绩的中位数是45分 D、该班学生这次考试成绩的平均数是45分7. 已知 , ,则 的值为( )A、-3 B、-1 C、1 D、58. 下面是四位同学所作的 关于直线 对称的图形,其中正确的是( )A、 B、
B、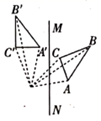 C、
C、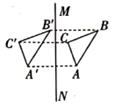 D、
D、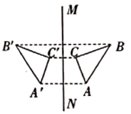 9. 如果方程组 的解是二元一次方程 的一个解,则m的值为( )A、2 B、 C、 D、10. 小强是一位密码编译爱好者,在他的密码手册中,有这样一条信息: ,a-b, , , , ,分别对应下列六个字:海、爱、我、美、游、北,现将 因式分解,结果呈现的密码信息可能是( )A、我爱游 B、北海游 C、我爱北海 D、美我北海
9. 如果方程组 的解是二元一次方程 的一个解,则m的值为( )A、2 B、 C、 D、10. 小强是一位密码编译爱好者,在他的密码手册中,有这样一条信息: ,a-b, , , , ,分别对应下列六个字:海、爱、我、美、游、北,现将 因式分解,结果呈现的密码信息可能是( )A、我爱游 B、北海游 C、我爱北海 D、美我北海二、填空题
-
11. 因式分解:a2﹣a=.12. 如图,将△AOB绕点O按逆时针方向旋转45°后得到△COD,若∠AOB=15°,则∠AOD=度.
 13. 如图,一张宽度相等的纸条,折叠后,若∠ABC=110°,则∠1的度数为.
13. 如图,一张宽度相等的纸条,折叠后,若∠ABC=110°,则∠1的度数为. 14. 已知 是完全平方式,则m的值为.15. 《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?设有x匹大马,y匹小马,根据题意可列方程组为 .
14. 已知 是完全平方式,则m的值为.15. 《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?设有x匹大马,y匹小马,根据题意可列方程组为 .
三、解答题
-
16. 计算: .17. 解方程组: .18. 先化简,再求值: ,其中 , .19. 如图,已知直线 , 相交于点O, , 平分 ,且 ,求 的度数.
 20. 如图,某市有一块长为 米,宽为 米的长方形地块,规划部门计划将阴影部分进行绿化,中间修建一座雕像,求绿化的面积是多少平方米?并求出当 时的绿化面积?
20. 如图,某市有一块长为 米,宽为 米的长方形地块,规划部门计划将阴影部分进行绿化,中间修建一座雕像,求绿化的面积是多少平方米?并求出当 时的绿化面积? 21. 如图,AB∥CD,∠B=70°,∠BCE=20°,∠CEF=130°,请判断AB与EF的位置关系,并说明理由.
21. 如图,AB∥CD,∠B=70°,∠BCE=20°,∠CEF=130°,请判断AB与EF的位置关系,并说明理由. 22. 小明到某服装专卖店去做社会调查,了解到该专卖店为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法计算薪资,并获得如下信息:
22. 小明到某服装专卖店去做社会调查,了解到该专卖店为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法计算薪资,并获得如下信息:营业员
小张
小王
月销售件数
200
150
月总收入/元
1400
1250
假设月销售件数为x,月总收入为y元,销售每件奖励a元,营业员月基本工资为b元.
(1)、求a、b的值.(2)、若营业员小张上个月总收入是1700元,则小张上个月卖了多少件服装?23. 如图 ,已知 , 在 的右侧, 平分 , 平分 , , 所在直线交于点 . (1)、求 的度数.(2)、若 ,求 的度数(用含 的代数式表示).(3)、将线段 沿 方向平移,使得点 在点 的右侧,其他条件不变,在图 中画出平移后的图形,并判断 的度数是否发生改变?若改变,求出它的度数(用含 的式子表示);若不改变,请说明理由.
(1)、求 的度数.(2)、若 ,求 的度数(用含 的代数式表示).(3)、将线段 沿 方向平移,使得点 在点 的右侧,其他条件不变,在图 中画出平移后的图形,并判断 的度数是否发生改变?若改变,求出它的度数(用含 的式子表示);若不改变,请说明理由.