吉林省四平市公主岭市2019-2020学年七年级下学期数学期中考试试卷
试卷更新日期:2020-06-17 类型:期中考试
一、单选题
-
1. 4的算术平方根是( )A、-2 B、2 C、 D、2. 在实数 , , , 中,无理数有( )A、1个 B、2个 C、3个 D、4个3. 如图,数轴上点P表示的数一定不可能是( )
 A、 B、 C、 D、4. 如图,在一次活动中,位于 处的七年一班准备前往相距 的 处与七年二班会合,若用方向和距离描述七年二班相对于七年一班的位置,可以描述为( )
A、 B、 C、 D、4. 如图,在一次活动中,位于 处的七年一班准备前往相距 的 处与七年二班会合,若用方向和距离描述七年二班相对于七年一班的位置,可以描述为( ) A、南偏西40°,3km B、南偏西50°,3km C、北偏东40°,3km D、北偏东50°,3km5. 下列各图中,∠1和∠2是对顶角的是( )A、
A、南偏西40°,3km B、南偏西50°,3km C、北偏东40°,3km D、北偏东50°,3km5. 下列各图中,∠1和∠2是对顶角的是( )A、 B、
B、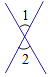 C、
C、 D、
D、 6. 下列命题中,是真命题的是( )A、互补的角是邻补角 B、相等的角是对顶角 C、同旁内角互补 D、两直线平行,内错角相等7. 如图,若在象棋盘上建立直角坐标系xOy,使“帥”位于点(-1,-2),“馬”位于点(2,-2),则“兵”位于点( )
6. 下列命题中,是真命题的是( )A、互补的角是邻补角 B、相等的角是对顶角 C、同旁内角互补 D、两直线平行,内错角相等7. 如图,若在象棋盘上建立直角坐标系xOy,使“帥”位于点(-1,-2),“馬”位于点(2,-2),则“兵”位于点( )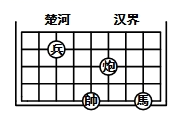 A、(-2,3) B、(-2,1) C、(-3,1) D、(-3,3)8. 已知a,b,c是三条直线,下列结论正确的是( )A、若a∥b,b∥c,则a∥c B、若a⊥b,b⊥c,则a⊥c C、若a∥b,b⊥c,则a∥c D、若a⊥b,b∥c,则a∥c
A、(-2,3) B、(-2,1) C、(-3,1) D、(-3,3)8. 已知a,b,c是三条直线,下列结论正确的是( )A、若a∥b,b∥c,则a∥c B、若a⊥b,b⊥c,则a⊥c C、若a∥b,b⊥c,则a∥c D、若a⊥b,b∥c,则a∥c二、填空题
-
9. 若 有意义,则a的值为(写出一个即可).10. 若一个正数的两个平方根分别为 和 ,则x的值为 .11. 如图,要在河的两岸搭建一座桥,在PA,PB,PC三种搭建方式中,最短的是PB,其理由是 .
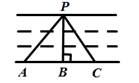 12. 如图,直线AB,CD被直线EF所截,如果∠2=100°,那么∠1的同位角等于度.
12. 如图,直线AB,CD被直线EF所截,如果∠2=100°,那么∠1的同位角等于度. 13. 若点P(x+1,x-3)在x轴上,则x的值为 .14. 如图,三角形ABC中任意一点P(x,y),经过平移后对应点为P1(x+5,y-1),将三角形ABC作同样的平移得到三角形A1B1C1 , 若点A的坐标为(-4,5),则点A1的坐标为 .
13. 若点P(x+1,x-3)在x轴上,则x的值为 .14. 如图,三角形ABC中任意一点P(x,y),经过平移后对应点为P1(x+5,y-1),将三角形ABC作同样的平移得到三角形A1B1C1 , 若点A的坐标为(-4,5),则点A1的坐标为 .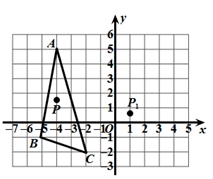 15. 请完成下面的解答过程.
15. 请完成下面的解答过程.如图,∠1=∠B,∠C=110°,求∠3的度数.
解:∵∠1=∠B,
∴AD∥()
∴∠C+=180°.(两直线平行,同旁内角互补)
∵∠C=110°,
∴∠2=°.
∴∠3==70°.()

三、解答题
-
16. 计算: .17. 计算: .18. 如图,将三角形ABC向下平移3个单位长度,可以得到三角形A1B1C1 .(1)、在坐标系中画出平移后的三角形A1B1C1;(2)、点B1的坐标为;(3)、线段AA1的长度为个单位长度.
 19. 如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.试说明:AC∥DF.
19. 如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.试说明:AC∥DF.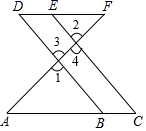 20. 如图①,将两个边长为1的小正方形分别沿对角线剪开,拼成正方形ABCD.
20. 如图①,将两个边长为1的小正方形分别沿对角线剪开,拼成正方形ABCD.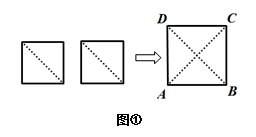
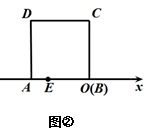 (1)、正方形ABCD的面积为 , 边长为 , 对角线BD=;(2)、求证: ;(3)、如图②,将正方形ABCD放在数轴上,使点B与原点O重合,边AB落在x轴的负半轴上,则点A所表示的数为 , 若点E所表示的数为整数,则点E所表示的数为21. 如图,直线AB,CD相交于点O,OM⊥AB.
(1)、正方形ABCD的面积为 , 边长为 , 对角线BD=;(2)、求证: ;(3)、如图②,将正方形ABCD放在数轴上,使点B与原点O重合,边AB落在x轴的负半轴上,则点A所表示的数为 , 若点E所表示的数为整数,则点E所表示的数为21. 如图,直线AB,CD相交于点O,OM⊥AB. (1)、∠AOC的邻补角为(写出一个即可);(2)、若∠1=∠2,判断ON与CD的位置关系,并说明理由;(3)、若∠1= ∠BOC,求∠MOD的度数.22. 如图,在长方形OABC中,O为平面直角坐标系的原点,点A,点C分别在x轴,y轴上,点B坐标为(4,6),点P从点O出发,以每秒2个单位长度的速度沿O→C→B方向运动,到点B停止.设点P运动的时间为t(秒).
(1)、∠AOC的邻补角为(写出一个即可);(2)、若∠1=∠2,判断ON与CD的位置关系,并说明理由;(3)、若∠1= ∠BOC,求∠MOD的度数.22. 如图,在长方形OABC中,O为平面直角坐标系的原点,点A,点C分别在x轴,y轴上,点B坐标为(4,6),点P从点O出发,以每秒2个单位长度的速度沿O→C→B方向运动,到点B停止.设点P运动的时间为t(秒). (1)、点A的坐标为;(2)、当t=1秒时,点P的坐标;(3)、当点P在OC上运动,请直接写出点P的坐标(用含有t的式子表示);(4)、在移动过程中,当点P到y轴的距离为1个单位长度时,求t的值.23. 如图,将三角形ABC沿射线BA方向平移到三角形A'B'C'的位置,连接AC'.
(1)、点A的坐标为;(2)、当t=1秒时,点P的坐标;(3)、当点P在OC上运动,请直接写出点P的坐标(用含有t的式子表示);(4)、在移动过程中,当点P到y轴的距离为1个单位长度时,求t的值.23. 如图,将三角形ABC沿射线BA方向平移到三角形A'B'C'的位置,连接AC'. (1)、AA'与CC'的位置关系为;(2)、求证:∠A'+∠CAC'+∠AC'C=180°;(3)、设 ∠ACB=y,试探索∠CAC'与x,y之间的数量关系,并证明你的结论.24. 问题情境:
(1)、AA'与CC'的位置关系为;(2)、求证:∠A'+∠CAC'+∠AC'C=180°;(3)、设 ∠ACB=y,试探索∠CAC'与x,y之间的数量关系,并证明你的结论.24. 问题情境:如图,在平面直角坐标系中有三点A(x1 , y1),B(x2 , y2),C(x3 , y3),小明在学习中发现,当x1=x2 , AB∥y轴,线段AB的长度为|y1﹣y2|;当y1=y3 , AC∥x轴,线段AC的长度为|x1﹣x3|.
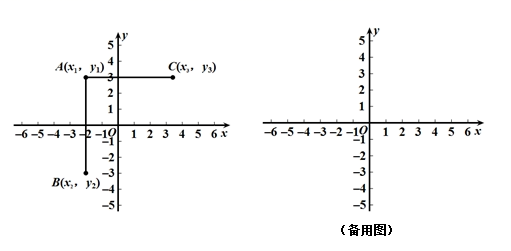 (1)、初步应用
(1)、初步应用若点A(﹣1,1)、B(2,1),则AB∥轴(填“x”或“y”);
(2)、若点C(1,﹣2),CD∥y轴,且点D在x轴上,则CD=;(3)、若点E(﹣3,2),点F(t,﹣4),且EF∥y轴,t=;(4)、拓展探索:已知P(3,﹣3),PQ∥y轴.
若三角形OPQ的面积为3,求满足条件的点Q的坐标.
(5)、若PQ=a,将点Q向右平移b个单位长度到达点M,已知点M在第一象限角平分线上,请直接写出a,b之间满足的关系.