上海市宝山区2019-2020学年九年级下学期数学期中考试试卷
试卷更新日期:2020-06-17 类型:期中考试
一、单选题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 关于 的方程 有实数根,则 的值的范围是( )A、 B、 C、 D、3. 为备战奥运会,甲、乙、丙、丁四位优秀短跑选手参加训练,近期的10次百米测试平均成绩都是10.3秒,但他们成绩的方差分别是0.020、0.019、0.021、0.022(单位:秒²)则这四人中发挥最稳定的是( )A、甲 B、乙 C、丙 D、丁4. 下列图形中,是中心对称但不是轴对称图形的是( )A、菱形 B、矩形 C、等腰梯形 D、平行四边形5. 如右图,矩形EFGH内接于△ABC,且边FG落在BC上,如果AD⊥BC,BC=3,AD=2,EF:EH=2:3,那么EH的长为( )
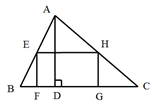 A、 B、 C、 D、26. 如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,如果点B的横坐标为x,点C的纵坐标为y,那么表示y与x的函数关系的图像大致是( )
A、 B、 C、 D、26. 如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,如果点B的横坐标为x,点C的纵坐标为y,那么表示y与x的函数关系的图像大致是( ) A、
A、 B、
B、 C、
C、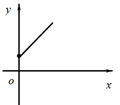 D、
D、
二、填空题
-
7. 2020的相反数是.8. 计算: .9. 分解因式: .10. 方程 的解是 .11. 一组数据3、12、8、12、20、9的众数为 .12. 一个不透明的盒子中装有9个大小相同的乒乓球,其中3个是黄球,6个是白球,从该盒子中任意摸出一个球,摸到白球的概率是 .13. 若抛物线y=(x﹣m)2+(m+1)的顶点在第二象限,则m的取值范围为 .14. 如图,点A的坐标是(2,0),△ABO是等边三角形,点B在第一象限,若反比例函数 的图象经过点B,则k的值是 .
 15. 在平行四边形 中,如果 , ,那么 , . (用 、 表示)16. 如图,点D是△ABC的边AB上一点,如果∠ACD=∠B,并且 ,那么 .
15. 在平行四边形 中,如果 , ,那么 , . (用 、 表示)16. 如图,点D是△ABC的边AB上一点,如果∠ACD=∠B,并且 ,那么 .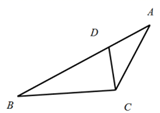 17. 如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,若AB=4,BC=2,那么线段EF的长为 .
17. 如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,若AB=4,BC=2,那么线段EF的长为 .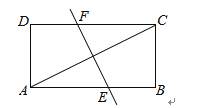 18. 如图,在△ABC中,AB=AC=5, ,将△ABC绕点B逆时针旋转,得到 ,当点 在线段CA延长线上时 的面积为 .
18. 如图,在△ABC中,AB=AC=5, ,将△ABC绕点B逆时针旋转,得到 ,当点 在线段CA延长线上时 的面积为 .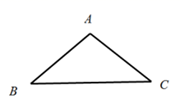
三、解答题
-
19. 计算:20. 解方程:21. 已知:如图,⊙O与⊙P相切于点 ,如果过点 的直线 交⊙O于点 ,交⊙P点 , ⊥ 于点 , ⊥ 于点 .
 (1)、求 的值:(2)、如果⊙O和⊙P的半径比为 ,求 的值.22. 在抗击新冠状病毒战斗中,有152箱公共卫生防护用品要运到 、 两城镇,若用大小货车共15辆,则恰好能一次性运完这批防护用品,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其中用大货车运往 、 两城镇的运费分别为每辆800元和900元,用小货车运往 、 两城镇的运费分别为每辆400元和600元.(1)、求这15辆车中大小货车各多少辆?(2)、现安排其中10辆货车前往 城镇,其余货车前往 城镇,设前往 城镇的大货车为 辆,前往 、 两城镇总费用为 元,试求出 与 的函数解析式.若运往 城镇的防护用品不能少于100箱,请你写出符合要求的最少费用.23. 如图, 分别是正方形 的边 的中点,以 为边作正方形 , 与 交于点 ,联结 .
(1)、求 的值:(2)、如果⊙O和⊙P的半径比为 ,求 的值.22. 在抗击新冠状病毒战斗中,有152箱公共卫生防护用品要运到 、 两城镇,若用大小货车共15辆,则恰好能一次性运完这批防护用品,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其中用大货车运往 、 两城镇的运费分别为每辆800元和900元,用小货车运往 、 两城镇的运费分别为每辆400元和600元.(1)、求这15辆车中大小货车各多少辆?(2)、现安排其中10辆货车前往 城镇,其余货车前往 城镇,设前往 城镇的大货车为 辆,前往 、 两城镇总费用为 元,试求出 与 的函数解析式.若运往 城镇的防护用品不能少于100箱,请你写出符合要求的最少费用.23. 如图, 分别是正方形 的边 的中点,以 为边作正方形 , 与 交于点 ,联结 .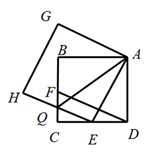 (1)、求证: ;(2)、设 ,求证 .24. 如图,在平面直角坐标系中,抛物线 与x轴交于A、B两点(点A在点B左侧),经过点A的直线 : 与 轴交于点C,与抛物线的另一个交点为D,且 .
(1)、求证: ;(2)、设 ,求证 .24. 如图,在平面直角坐标系中,抛物线 与x轴交于A、B两点(点A在点B左侧),经过点A的直线 : 与 轴交于点C,与抛物线的另一个交点为D,且 .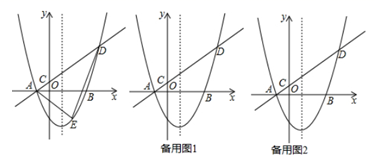 (1)、直接写出点A的坐标,并用含a的式子表示直线l的函数表达式(其中k、b用含a的式子表示).(2)、点E为直线l下方抛物线上一点,当 的面积的最大值为 时,求抛物线的函数表达式;(3)、设点P是抛物线对称轴上的一点,点Q在抛物线上,以点A、D、P、Q为顶点的四边形能否为矩形?若能,求出点P的坐标;若不能,请说明理由.25. 如图,已知:在直角 中, ,点 在边 上,且 如果将 沿 所在的直线翻折,点 恰好落在边 上的点 处,点 为 边上的一个动点,联结 ,以 圆心, 为半径作⊙ ,交线段 于点 和点 ,作 交⊙ 于点 , 交线段 于点 .
(1)、直接写出点A的坐标,并用含a的式子表示直线l的函数表达式(其中k、b用含a的式子表示).(2)、点E为直线l下方抛物线上一点,当 的面积的最大值为 时,求抛物线的函数表达式;(3)、设点P是抛物线对称轴上的一点,点Q在抛物线上,以点A、D、P、Q为顶点的四边形能否为矩形?若能,求出点P的坐标;若不能,请说明理由.25. 如图,已知:在直角 中, ,点 在边 上,且 如果将 沿 所在的直线翻折,点 恰好落在边 上的点 处,点 为 边上的一个动点,联结 ,以 圆心, 为半径作⊙ ,交线段 于点 和点 ,作 交⊙ 于点 , 交线段 于点 . (1)、求点 到点 和直线 的距离(2)、如果点 平分劣弧 ,求此时线段 的长度(3)、如果 为等腰三角形,以 为圆心的⊙ 与此时的⊙ 相切,求⊙ 的半径
(1)、求点 到点 和直线 的距离(2)、如果点 平分劣弧 ,求此时线段 的长度(3)、如果 为等腰三角形,以 为圆心的⊙ 与此时的⊙ 相切,求⊙ 的半径