黑龙江省齐齐哈尔市2019-2020学年九年级下学期数学期中考试试卷
试卷更新日期:2020-06-17 类型:期中考试
一、单选题
-
1. ﹣3的绝对值是( )A、﹣3 B、3 C、- D、2. 下列“组织的有关图标”图片中,不是轴对称图形的是( ).A、
 B、
B、 C、
C、 D、
D、 3. 关于反比例函数y=
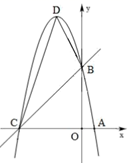
3. 关于反比例函数y= 图象,下列说法正确的是( ) A、必经过点(1,1) B、两个分支分布在第二、四象限 C、两个分支关于x轴成轴对称 D、两个分支关于原点成中心对称4. 如图,A,B,C三点在数轴上所表示的数分别为a、b、c.根据图中各点的位置,下列各式正确的为( ).
图象,下列说法正确的是( ) A、必经过点(1,1) B、两个分支分布在第二、四象限 C、两个分支关于x轴成轴对称 D、两个分支关于原点成中心对称4. 如图,A,B,C三点在数轴上所表示的数分别为a、b、c.根据图中各点的位置,下列各式正确的为( ). A、 B、 C、 D、5. 如图, 为 的内接三角形,AB为 的直径,点D在 上, ,则 的度数为( ).
A、 B、 C、 D、5. 如图, 为 的内接三角形,AB为 的直径,点D在 上, ,则 的度数为( ). A、 B、 C、 D、6. 下列调查,比较适用普查而不适用抽样调查方式的是( ).A、调查全省市场上的“N95口罩”是否符合国家标准 B、调查一批灯泡的使用寿命 C、调查你所在班级全体学生的身高 D、调查我市初中生每人每周的零花钱数7. 下列四个命题中,错误的命题是( ).A、四条边都相等的四边形是菱形; B、对角线互相垂直平分的四边形是正方形; C、有三个角是直角的四边形是矩形; D、一组对边平行且相等,对角线垂直且相等的四边形是正方形.8. 今年体育学业考试增加了跳绳测试项目,下面是测试时记录员记录的一组(10名)同学的测试成绩(单位:个/分钟).
A、 B、 C、 D、6. 下列调查,比较适用普查而不适用抽样调查方式的是( ).A、调查全省市场上的“N95口罩”是否符合国家标准 B、调查一批灯泡的使用寿命 C、调查你所在班级全体学生的身高 D、调查我市初中生每人每周的零花钱数7. 下列四个命题中,错误的命题是( ).A、四条边都相等的四边形是菱形; B、对角线互相垂直平分的四边形是正方形; C、有三个角是直角的四边形是矩形; D、一组对边平行且相等,对角线垂直且相等的四边形是正方形.8. 今年体育学业考试增加了跳绳测试项目,下面是测试时记录员记录的一组(10名)同学的测试成绩(单位:个/分钟).176 180 184 180 170 176 172 164 186 180
该组数据的众数、中位数、平均数分别为( )
A、180,180,178 B、180,178,178 C、180,178,176.8 D、178,180,176.89. 为了建设社会主义新农村,我市积极推进“行政村通畅工程”,对甲村和乙村之间的道路需要进行改造,施工队在工作了一段时间后,因暴雨被迫停工几天,不过施工队随后加快了施工进度,按时完成了两村之间道路的改造.下面能反映该工程改造道路里程 (公里)与时间 (天)的函数关系大致的图像是( ).A、 B、
B、 C、
C、 D、
D、 10. 如图,二次函数 的图象与y轴正半轴相交,其顶点坐标为 ,下列结论:① ;② ;③ ;④ .其中正确的个数是( ).
10. 如图,二次函数 的图象与y轴正半轴相交,其顶点坐标为 ,下列结论:① ;② ;③ ;④ .其中正确的个数是( ).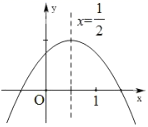 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 中国是严重缺水的国家之一,人均淡水资源为世界人均量的四分之一,所以我们要为中国节水,为世界节水.若每人每天浪费水0.32升,那么100万人每天浪费的水,用科学记数法表示为升.12. 在一个不透明的口袋中,装有5个红球3个白球,它们除颜色外都相同,从中任意摸出一个球,摸到红球的概率为13. 已知 ,且 为锐角,则m的取值范围是 .14. 一个等腰三角形的两边长分别为5cm和6cm,则该等腰三角形的周长为cm.15. 如图,P为线段AB上一点,AD与BC交于E, ,BC交PD于F,AD交PC于G,则图中相似三角形有对.
 16. 矩形 中, , ,点E、点F在直线AD上,且四边形BCFE为菱形,若点M为线段EF的中点,则线段AM的长为 .17. 如图,在 中, , , ,以 为边作 ,使 , ;再以 为边作 ,使 , ;再以 为边作 ,使 , ,…,如此继续,可以依次得到 , , ,…, ,则 .
16. 矩形 中, , ,点E、点F在直线AD上,且四边形BCFE为菱形,若点M为线段EF的中点,则线段AM的长为 .17. 如图,在 中, , , ,以 为边作 ,使 , ;再以 为边作 ,使 , ;再以 为边作 ,使 , ,…,如此继续,可以依次得到 , , ,…, ,则 .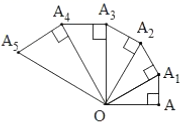
三、解答题
-
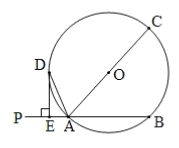
18. 计算: .19. 分解因式: .20. 解方程: .21. 如图,直线PAB交 于A、B两点,AC是 的直径, 的平分线交 于点D,过点D作 于点D.(1)、求证:DE为 的切线;(2)、若 , 的直径为10,求AB的长度.
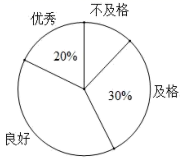
 22. 新冠肺炎疫情发生以来,专家给出了很多预防建议.为普及预防措施,某校组织了由八年级800名学生参加的“防新冠”知识竞赛.李老师为了了解学生的答题情况,从中随机抽取了部分同学的成绩作为样本,把成绩按优秀、良好、及格、不及格4个级别进行统计,并绘制成了如图的条形统计图和扇形统计图(部分信息未给出).
22. 新冠肺炎疫情发生以来,专家给出了很多预防建议.为普及预防措施,某校组织了由八年级800名学生参加的“防新冠”知识竞赛.李老师为了了解学生的答题情况,从中随机抽取了部分同学的成绩作为样本,把成绩按优秀、良好、及格、不及格4个级别进行统计,并绘制成了如图的条形统计图和扇形统计图(部分信息未给出).请根据以上提供的信息,解答下列问题:
(1)、求被抽取的部分学生的人数;(2)、请补全条形统计图;(3)、求出扇形统计图中表示良好级别的扇形的圆心角度数;(4)、请估计八年级的800名学生中达到良好和优秀的总人数.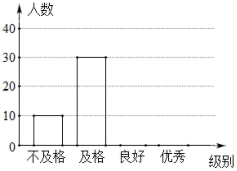
 23. 某地区在同一直线上依次有甲、乙、丙三座城市一列快车从甲市出发匀速行驶开往丙市,一列动车从丙市出发匀速行驶往返于乙、丙两座城市,两列火车同时出发.如图是两列火车距甲市的路程y(千米)与行驶时间x(小时)之间的函数图象,请你结合图像信息解决下列问题:(1)、直接写出:甲、乙两市相距千米,图像中a的值为 , b的值;(2)、求动车从乙地返回多长时间时与快车相遇?(3)、请直接写出快车出发多长时间两列火车(都在行驶时)相距30千米?
23. 某地区在同一直线上依次有甲、乙、丙三座城市一列快车从甲市出发匀速行驶开往丙市,一列动车从丙市出发匀速行驶往返于乙、丙两座城市,两列火车同时出发.如图是两列火车距甲市的路程y(千米)与行驶时间x(小时)之间的函数图象,请你结合图像信息解决下列问题:(1)、直接写出:甲、乙两市相距千米,图像中a的值为 , b的值;(2)、求动车从乙地返回多长时间时与快车相遇?(3)、请直接写出快车出发多长时间两列火车(都在行驶时)相距30千米?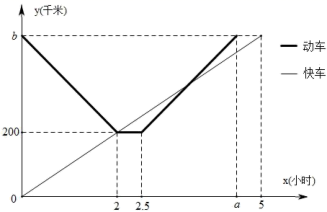 24. 综合与实践
24. 综合与实践动手实践:数学课上老师让学生们折矩形纸片下面几幅图是学生们折出的一部分图形(沿直线l折叠)由于折痕所在的直线不同,折出的图形也不同,各个图形中所“隐含的”基本图形也不同.我们可以通过发现基本图形研究这些图形中几何问题.
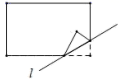

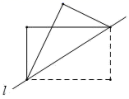
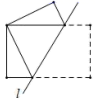 (1)、问题解决:
(1)、问题解决:
如图1,将矩形纸片ABCD沿直线MN折叠,使得点C与点A重合,点D落在点 的位置,连接MC,AN,AC,线段AC交MN于点O,则 与 的关系为 , 线段AC与线段MN的关系为 . 小强量得 ,则 .小丽说:“四边形 是菱形”,请你帮她证明.
 (2)、拓展延伸:
(2)、拓展延伸:
如图2,矩形纸片ABCD中, , ,小明将矩形纸片ABCD沿直线AM折叠,点B落在点 的位置, 交AD于点N,请你直接写出线段ND的长: .
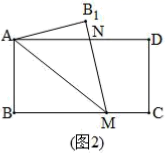 (3)、综合探究:
(3)、综合探究:
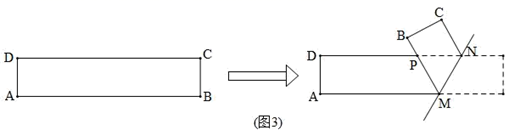
如图3,ABCD是一张矩形纸片, , .在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使线段MB与线段DN交于点P,得到 .请你确定 面积的取值范围。
 25. 综合与探究
25. 综合与探究已知:p、q是方程 的两个实数根,且 ,抛物线 的图像经过点 、 .
(1)、求这个抛物线的解析式;(2)、设(1)中抛物线与 轴的另一交点为C,抛物线的顶点为D,试求出点C、D的坐标和 的面积;(3)、P是线段OC上的一点,过点P作 轴,与抛物线交于H点,若直线BC把 分成面积之比为 的两部分,请直接写出P点的坐标;(4)、若点M在直线CB上,点N在平面上,直线CB上是否存在点M,使以点C、点D、点M、点N为顶点的四边形为菱形?若存在,请直接写出点M的坐标;若不存在,请说明理由.