广东省汕头市潮南区2020年中考数学模拟试卷
试卷更新日期:2020-06-16 类型:中考模拟
一、选择题
-
1. 2020的相反数是( )A、 B、﹣ C、|2020| D、﹣20202. 下列四个图形中,既是轴对称图形又是中心对称图形的是( )A、等边三角形 B、菱形 C、平行四边形 D、正五边形3. 下列各式中,计算结果为a6的是( )A、a2+a4 B、a8﹣a2 C、a2•a3 D、a7÷a4. 港珠澳大桥于2018年10月24日正式通车,该工程总投资额为1269亿元,将1269亿用科学记数法表示为( )A、1.269×1011 B、12.69×1010 C、1.269×1012 D、0.1269×10135. 化简 的结果是( )A、 B、
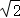 C、
D、
6. 某校为了丰富校园文化,举行初中生书法大赛,决赛设置了7个获奖名额,共有13名选手进入决赛,选手决赛得分均不相同,小颖知道自己的比赛分数后,要判断自己能否获奖,需要知道这13名同学成绩的( )A、众数 B、中位数 C、平均数 D、方差7. 下列四个图形中,不是正方体展开图的( )A、
C、
D、
6. 某校为了丰富校园文化,举行初中生书法大赛,决赛设置了7个获奖名额,共有13名选手进入决赛,选手决赛得分均不相同,小颖知道自己的比赛分数后,要判断自己能否获奖,需要知道这13名同学成绩的( )A、众数 B、中位数 C、平均数 D、方差7. 下列四个图形中,不是正方体展开图的( )A、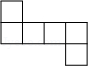 B、
B、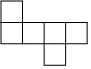 C、
C、 D、
D、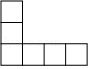 8. 关于x的一元二次方程kx2+2x+1=0有实数根,则实数k的取值范围是( )A、k≤1 B、k<1 C、k≤1且k≠0 D、k<1且k≠09. 如图是一组有规律的图案,它们是由边长相同的正方形和正三角形拼接而成,第①个图案有4个三角形,第②个图案有7个三角形,第③个图案有10个三角形,…依此规律,第2019个图案有多少个三角形( )
8. 关于x的一元二次方程kx2+2x+1=0有实数根,则实数k的取值范围是( )A、k≤1 B、k<1 C、k≤1且k≠0 D、k<1且k≠09. 如图是一组有规律的图案,它们是由边长相同的正方形和正三角形拼接而成,第①个图案有4个三角形,第②个图案有7个三角形,第③个图案有10个三角形,…依此规律,第2019个图案有多少个三角形( )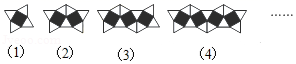 A、6068 B、6058 C、6048 D、705810. 如图,已知D、E、F分别是等边△ABC的边AB、BC、AC上的点,且DE⊥BC、EF⊥AC、FD⊥AB , 则下列结论不成立的是( )
A、6068 B、6058 C、6048 D、705810. 如图,已知D、E、F分别是等边△ABC的边AB、BC、AC上的点,且DE⊥BC、EF⊥AC、FD⊥AB , 则下列结论不成立的是( )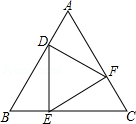 A、△DEF是等边三角形 B、△ADF≌△BED≌△CFE C、DE=
A、△DEF是等边三角形 B、△ADF≌△BED≌△CFE C、DE=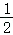 AB
D、S△ABC=3S△DEF
AB
D、S△ABC=3S△DEF
二、填空题
-
11. 分解因式:2x3﹣8x .12. 若
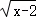 +(3﹣y)2=0,那么yx= .
13. 如果正多边形的一个内角等于135°,那么这个正多边形的边数是.14. 若代数式x2+x+3的值的值为7,则代数式 的值为 .15. △ABC与△DEF相似,其面积比为1:4,则它们的相似比为.16. 解不等式组
+(3﹣y)2=0,那么yx= .
13. 如果正多边形的一个内角等于135°,那么这个正多边形的边数是.14. 若代数式x2+x+3的值的值为7,则代数式 的值为 .15. △ABC与△DEF相似,其面积比为1:4,则它们的相似比为.16. 解不等式组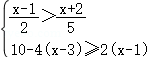 ,它的解集为.
17. 如图,AB是半圆O的直径,且AB=12,点C为半圆上的一点.将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O , 则图中阴影部分的面积是 . (结果保留π)
,它的解集为.
17. 如图,AB是半圆O的直径,且AB=12,点C为半圆上的一点.将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O , 则图中阴影部分的面积是 . (结果保留π)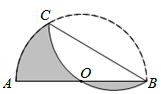
三、解答题
-
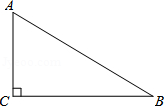
18. 计算:19.20. 如图,在Rt△ABC中,∠ACB=90°.(1)、用尺在边AB上求作一点P , 使PC=PB , 并连接PC;(不写作法,保留作图痕迹)(2)、当AC=3,BC=4时,△ACP的周长=;
四、解答题
-
21. 中国的数字支付正在引领未来世界的支付方式变革。某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
30
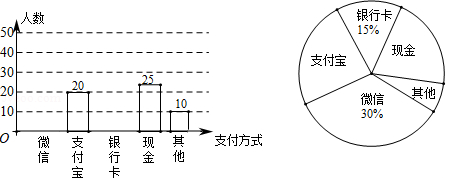 (1)、这次活动共调查了人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为;(2)、将条形统计图补充完整 . 观察此图,将各种支付方式调查人数组成一组数据,求这组数据的“中位数”是;(3)、在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表的方法,求两人选同种支付方式的概率.22. 如图,在线段BC上有两点E , F , 在线段CB的异侧有两点A , D , 满足AB=CD , AE=DF , CE=BF , 连接AF;
(1)、这次活动共调查了人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为;(2)、将条形统计图补充完整 . 观察此图,将各种支付方式调查人数组成一组数据,求这组数据的“中位数”是;(3)、在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表的方法,求两人选同种支付方式的概率.22. 如图,在线段BC上有两点E , F , 在线段CB的异侧有两点A , D , 满足AB=CD , AE=DF , CE=BF , 连接AF;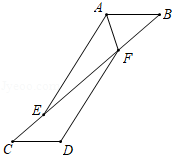 (1)、连接DE,求证:四边形AEDF是平行四边形;(2)、若∠B=40°,∠DFC=30°,当AF平分∠BAE时,求∠BAF .23. “六一”儿童节前,玩具商店根据市场调查,用2500元购进一批儿童玩具,上市后很快脱销,接着又用4500元购进第二批这种玩具,所购数量是第一批数量的1.5倍,但每套进价多了10元.第一、二批玩具每套的进价分别是多少元?
(1)、连接DE,求证:四边形AEDF是平行四边形;(2)、若∠B=40°,∠DFC=30°,当AF平分∠BAE时,求∠BAF .23. “六一”儿童节前,玩具商店根据市场调查,用2500元购进一批儿童玩具,上市后很快脱销,接着又用4500元购进第二批这种玩具,所购数量是第一批数量的1.5倍,但每套进价多了10元.第一、二批玩具每套的进价分别是多少元?五、解答题
-
24. 如图,在Rt△ABC中,∠ABC=90°,AB=CB , 以AB为直径的⊙O交AC于点D , 点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G , DF⊥DG , 且交BC于点F .
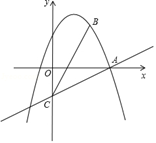
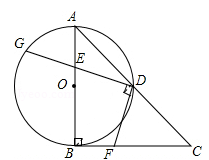 (1)、求证:AE=BF;(2)、连接EF , 求证:∠FEB=∠GDA;(3)、连接GF , 若AE=2,EB=4,求△GFD的面积.25. 如图,在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c经过点A(3,0)和点B(2,3),过点A的直线与y轴的负半轴相交于点C , 且tan∠CAO=
(1)、求证:AE=BF;(2)、连接EF , 求证:∠FEB=∠GDA;(3)、连接GF , 若AE=2,EB=4,求△GFD的面积.25. 如图,在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c经过点A(3,0)和点B(2,3),过点A的直线与y轴的负半轴相交于点C , 且tan∠CAO=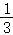 .
. 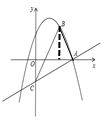 (1)、求这条抛物线的表达式及对称轴;(2)、连接AB、BC , 求∠ABC的正切值;(3)、若点D在x轴下方的对称轴上,当S△DBC=S△ADC时,求点D的坐标.
(1)、求这条抛物线的表达式及对称轴;(2)、连接AB、BC , 求∠ABC的正切值;(3)、若点D在x轴下方的对称轴上,当S△DBC=S△ADC时,求点D的坐标.