浙江省温州市乐清市2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-06-15 类型:期末考试
一、选择题
-
1. 下列视力表的部分图案中,既是轴对称图形亦是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若二次根式 有意义,则x的取值范围为( )A、x≥3 B、x≠3 C、x>3 D、x≤33. 五边形的内角和是( )A、180° B、360° C、540° D、720°4. 某班18名男生参加中考体育模拟测试,1000m跑步项目成绩如下表:
2. 若二次根式 有意义,则x的取值范围为( )A、x≥3 B、x≠3 C、x>3 D、x≤33. 五边形的内角和是( )A、180° B、360° C、540° D、720°4. 某班18名男生参加中考体育模拟测试,1000m跑步项目成绩如下表:成绩(分)
人数
则该班男生成绩的中位数是( )
A、7 B、7.5 C、8 D、95. 用配方法解方程 ,下列配方正确的是( )A、 B、 C、 D、6. 用反证法证明命题“若 ,则 ”时,第一步应假设( )A、 B、 C、 D、7. 下列命题是真命题的是( )A、对角线互相垂直的四边形是菱形 B、对角线相等的菱形是正方形 C、对角线互相垂直且相等的四边形是正方形 D、对角线相等的四边形是矩形8. 反比例函数 的图象如图所示,则k的值可能是( )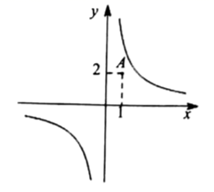 A、 B、 C、 D、9. 如图,在正方形 中,E为边 上一点,将 沿 折叠至 处, 与 交于点F,若 ,则 的大小为( )
A、 B、 C、 D、9. 如图,在正方形 中,E为边 上一点,将 沿 折叠至 处, 与 交于点F,若 ,则 的大小为( )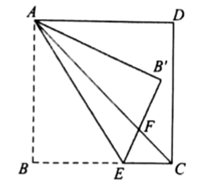 A、 B、 C、 D、10. 在平面直角坐标系中,反比例函数 的图象上有三点 ,若 且 ,则B的取值范围为( )A、 B、 C、 D、
A、 B、 C、 D、10. 在平面直角坐标系中,反比例函数 的图象上有三点 ,若 且 ,则B的取值范围为( )A、 B、 C、 D、二、填空题
-
11. 当 时,二次根式 的值是 .12. 甲,乙,丙三位同学近5次快速阅读模拟比赛成绩平均分均为86分,且甲,乙,丙的方差是 ,则发挥最稳定的同学是.13. 若关于x的方程 有实数根,则m的值可以是(写出一个即可)14. 如图,在矩形ABCD中,E、F分别是边AD和CD的中点,EF=3,则BD的长为.
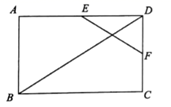 15. 如图,在平行四边形 中, , 的平分线 交 于点E,连接 ,若 ,则平行四边形 的面积为.
15. 如图,在平行四边形 中, , 的平分线 交 于点E,连接 ,若 ,则平行四边形 的面积为. 16. 如图,正方形 面积为1,延长 至点G,使得 ,以 为边在正方形另一侧作菱形 ,其中 ,依次延长 类似以上操作再作三个形状大小都相同的菱形,形成风车状图形,依次连结点 则四边形 的面积为.
16. 如图,正方形 面积为1,延长 至点G,使得 ,以 为边在正方形另一侧作菱形 ,其中 ,依次延长 类似以上操作再作三个形状大小都相同的菱形,形成风车状图形,依次连结点 则四边形 的面积为.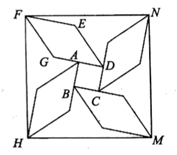
三、解答题
-
17.(1)、计算:(2)、解方程:18. 某校举办的八年级学生数学素养大赛共设 个项目:七巧板拼图,趣题巧解,数学应用,每个项目得分都按一定百分比折算后计入总分,总分高的获胜,下表为小米和小麦两位同学的得分情况(单位:分):
七巧板拼图
趣题巧解
数学应用
小米
80
90
88
小麦
90
86
85
(1)、若七巧板拼图,趣题巧解,数学应用三项得分分别 按折算计入总分,最终谁能获胜?(2)、若七巧板拼图按 折算,小麦 (填“可能”或“不可能”)获胜.19. 如图,在平行四边形ABCD中,AC是它的一条对角线,BE⊥AC于点E,DF⊥AC于点F,求证:四边形BEDF是平行四边形.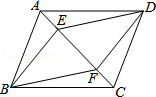 20. 如图,在 的方格纸中,每一个小正方形的边长均为1,点 在格点上,用无刻度直尺按下列要求作图,保留必要的作图痕迹.
20. 如图,在 的方格纸中,每一个小正方形的边长均为1,点 在格点上,用无刻度直尺按下列要求作图,保留必要的作图痕迹. (1)、在图1中,以 为边画一个正方形 ;(2)、在图2中,以 为边画一个面积为5的矩形 ( 可以不在格点上).21. 如图,在平面直角坐标系中,菱形 的顶点 在反比例函数 图象上,直线 交 于点 ,交 正半轴于点 ,且
(1)、在图1中,以 为边画一个正方形 ;(2)、在图2中,以 为边画一个面积为5的矩形 ( 可以不在格点上).21. 如图,在平面直角坐标系中,菱形 的顶点 在反比例函数 图象上,直线 交 于点 ,交 正半轴于点 ,且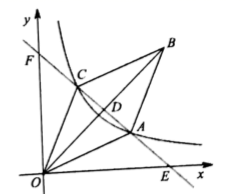 (1)、求 的长:(2)、若 ,求k的值.22. 市政规划出一块矩形土地用于某项目开发,其中 ,设计分区如图所示,E为矩形内一点,作 于点 交 于点F,H过点 作 交 于点I,其中丙区域用于主建筑区,其余各区域均用于不同种类绿化.
(1)、求 的长:(2)、若 ,求k的值.22. 市政规划出一块矩形土地用于某项目开发,其中 ,设计分区如图所示,E为矩形内一点,作 于点 交 于点F,H过点 作 交 于点I,其中丙区域用于主建筑区,其余各区域均用于不同种类绿化. (1)、若点G是 的中点,求 的长;(2)、要求绿化占地面积不小于 ,规定乙区域面积为
(1)、若点G是 的中点,求 的长;(2)、要求绿化占地面积不小于 ,规定乙区域面积为①若将甲区域设计成正方形形状,能否达到设计绿化要求?请说明理由;
②若主建筑丙区域不低于乙区域面积的 ,则 的最大值为 ▲ m (请直接写出答案)
23. 如图, , 点 分别在线段 上,且 (1)、求证:(2)、已知 分别是 的中点,连结
(1)、求证:(2)、已知 分别是 的中点,连结①若 ,求 的度数:
②连结 当 的长为何值时,四边形 是矩形?