浙江省绍兴市柯桥区2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2020-06-15 类型：期末考试

进入出卷网下载

一、选择题

1. 若二次根式 $\sqrt{x - 3}$ 有意义，则x的取值范围为（）

A、x≥3 B、x≠3 C、x>3 D、x≤3

查看试题解析
2. 下列图形中，是中心对称图形但不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 某农科院对甲、乙两种甜玉米各用10块相同条件的试验田进行试验，得到两个品种每公顷产量的两组数据，其方差分别为s_甲²＝0.002、s_乙²＝0.03，则（）

A、甲比乙的产量稳定 B、乙比甲的产量稳定 C、甲、乙的产量一样稳定 D、无法确定哪一品种的产量更稳定

查看试题解析
4. 用配方法解一元二次方程x²-8x+2=0，此方程可化为的正确形式是（）.

A、（x-4）²=14 B、（x-4）²=18 C、（x+4）²=14 D、（x+4）²=18

查看试题解析
5. 如图，小明在作线段AB的垂直平分线时，他是这样操作的：分别以A和B为圆心，大于 $\frac{1}{2} A B$ 的长为半径画弧，两弧相交于C，D两点，直线CD即为所求.根据他的作图方法可知四边形 $A B C D$ 一定是（）

A、矩形 B、菱形 C、正方形 D、无法确定

查看试题解析
6. 如图，四边形ABCD是正方形，延长AB到点E，使AE=AC，则∠BCE的度数是（）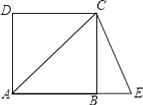

A、22.5° B、25° C、23° D、20°

查看试题解析
7. 用反证法证明命题：“四边形中至少有一个角是钝角或直角”时，首先应该假设这个四边形中（）

A、有一个角是钝角或直角 B、每一个角都是钝角 C、每一个角都是直角 D、每一个角都是锐角

查看试题解析
8. 如图，在长为32m ，宽为20m的矩形空地上修建同样宽的道路（图中阴影部分），剩余的空地上种植草坪，使草坪的面积为540m² ．设道路的宽为xm ，根据题意，下面列出的方程正确的是（）

A、32x+20x﹣2x²＝540 B、32x+20x＝32×20﹣540 C、（32﹣x）（20﹣x）＝540 D、（32﹣x）（20﹣x）＝32×20﹣540

查看试题解析
9. 如图，在Rt△ABC中，AC＝6，BC＝8，D为斜边AB上一动点，DE⊥BC，DF⊥AC，垂足分别为E、F.则线段EF的最小值为（）

A、6 B、 $\frac{12}{5}$ C、5 D、 $\frac{24}{5}$

查看试题解析
10. 如图，在直角坐标系中，正方形OABC的顶点O与原点重合，顶点A，C分别在x轴、y轴上，反比例函数y= $\frac{k}{x}$ (k≠0，x>0)的图象与正方形的两边AB、BC分别交于点E、F，FD⊥x轴，垂足为D，连接OE，OF，EF，FD与OE相交于点G.下列结论：①OF=OE；②∠EOF=60^°；③四边形AEGD与△FOG面积相等；④EF=CF+AE；⑤若∠EOF=45^° ， EF=4，则直线FE的函数解析式为 $y = - x + 4 + 2 \sqrt{2}$ .其中正确结论的个数是（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

11. 计算 $\sqrt{32}$ - $\sqrt{8}$ =.

查看试题解析
12. 我市某一周每天的最低气温统计如下（单位：℃）：﹣1，﹣4，6，0，﹣1，1，﹣1，则这组数据的众数为.

查看试题解析
13. 一个多边形的内角和与外角和的比是4：1，则它的边数是．

查看试题解析
14. 如图，若菱形ABCD的顶点A，B的坐标分别为（3，0），（﹣2，0），点D在y轴上，则点C的坐标是．

查看试题解析
15. 如果关于x的一元二次方程x²﹣6x+c=0（c是常数）没有实根，那么c的取值范围是.

查看试题解析
16. 如图，在矩形ABCD中，AB=6cm，BC=8cm，现将其沿EF对折，使得点C与点A重合，点D落在 $D^{'}$ 处，AF的长为.

查看试题解析
17. 如图，在平行四边形ABCD中，BE、CE分别平分∠ABC、∠BCD，E在AD上，BE=12cm，CE=5cm，则平行四边形ABCD的周长.

查看试题解析
18. 对于实数a，b，定义运算“*”，a*b＝ ${\begin{cases} a^{2} - a b (a > b) \\ a b - b^{2} (a \leq b) \end{cases}$ 例如4*2．因为4＞2，所以4*2＝4²－4×2＝8，若x₁、x₂是一元二次方程x²－9x＋20＝0的两个根，则x₁*x₂＝．

查看试题解析
19. 如图，在直角坐标系中，有菱形OABC，A点的坐标是（5，0），双曲线 $y = \frac{k}{x} (k > 0)$ 经过点C，且OB•AC=40，则k的值为 .

查看试题解析
20. 如图，四边形 $A B C P$ 是边长为4的正方形，点E在边 $C P$ 上，PE=1；作EF∥BC，分别交AC、AB于点G、F，M、N分别是AG、BE的中点，则MN的长是.

查看试题解析

三、解答题

21. 计算：

(1)、 $\sqrt{48} - 3 \sqrt{27} + \sqrt{\frac{1}{3}}$ ；

(2)、 $\sqrt{49}$ +（3﹣2 $\sqrt{3}$ ）（3+2 $\sqrt{3}$ ）

查看试题解析
22. 解方程：

(1)、 $y^{2} - 4 y = 12$

(2)、 $3 x (2 x + 1) = 2 (2 x + 1)$

查看试题解析

23. 随着我国经济社会的发展，人民对于美好生活的追求越来越高，外出旅游已成为时尚.某社区为了了解家庭旅游消费情况，随机抽取部分家庭，对每户家庭的年旅游消费金额进行问卷调査，根据调查结果绘制成两幅不完整的统计图表.请你根据统计图表提供的信息，解答下列问题：

组别	家庭年旅游消费金额x(元)	户数
A	x≤4000	27
B	4000< x≤8000	a
C	8000< x≤12000	24
D	12000< x≤16000	14
E	x>16000	6

(1)、本次被调査的家庭有户，表中 a=；

(2)、本次调查数据的中位数出现在组.扇形统计图中，E组所在扇形的圆心角是度；

(3)、若这个社区有2700户家庭，请你估计家庭年旅游消费8000元以上的家庭有多少户？

查看试题解析

24. 如图，E，F是正方形ABCD的对角线AC上的两点，且AE＝CF.

(1)、求证：四边形BEDF是菱形；

(2)、)若正方形ABCD的边长为4，AE＝ $\sqrt{2}$ ，求菱形BEDF的面积.

查看试题解析
25. 物美商场于今年年初以每件25元的进价购进一批商品．当商品售价为40元时，一月份销售256件．二、三月该商品十分畅销．销售量持续走高．在售价不变的基础上，三月底的销售量达到400件．设二、三这两个月月平均增长率不变．

(1)、求二、三这两个月的月平均增长率；

(2)、从四月份起，商场决定采用降价促销的方式回馈顾客，经调查发现，该商品每降价1元，销售量增加5件，当商品降价多少元时，商场获利4250元？

查看试题解析
26. 如图.已知A、B两点的坐标分别为A(0， $2 \sqrt{3}$ )，B(2，0).直线AB与反比例函数 $y = \frac{k}{x}$ 的图象交于点C和点D( $-$ 1，a).

(1)、求直线AB和反比例函数的解析式.

(2)、求∠ACO的度数.

查看试题解析
27. 类比等腰三角形的定义，我们定义：有三条边相等的凸四边形叫做“准等边四边形”.

(1)、已知：如图1，在“准等边四边形”ABCD中，BC≠AB，BD⊥CD，AB=3，BD=4，求BC的长；

(2)、在探究性质时，小明发现一个结论：对角线互相垂直的“准等边四边形”是菱形.请你判断此结论是否正确，若正确，请说明理由；若不正确，请举出反例；

(3)、如图2，在△ABC中，AB=AC= $\sqrt{2}$ ，∠BAC=90°.在AB的垂直平分线上是否存在点P，使得以A，B，C，P为顶点的四边形为“准等边四边形”. 若存在，请求出该“准等边四边形”的面积；若不存在，请说明理由.

查看试题解析