浙江省衢州地区2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-06-15 类型:期末考试
一、选择题
-
1. 中国传统扇文化有着深厚的底蕴,下列扇面图形是中心对称图形的是( )A、
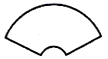 B、
B、 C、
C、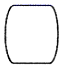 D、
D、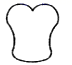 2. 根据《九章算术》的记载中国人最早使用负数,下列四个数中的负数是( )A、 B、 C、 D、3. 我市某一周每天的最高气温统计如下(单位:℃):27,28,29,28,29,30,29.这组数据的众数与中位数分别是( ).A、28,28 B、28,29 C、29,28 D、29,294. 矩形的边长是 ,一条对角线的长是 ,则矩形的面积是( )A、 B、 C、 . D、5. 若 的两根分别是 与5,则多项式 可以分解为( )A、 B、 C、 D、6. 如图,四边形ABCD的对角线AC,BD相交于点O,且AB∥CD,添加下列条件后仍不能判断四边形ABCD是平行四边形的是( )
2. 根据《九章算术》的记载中国人最早使用负数,下列四个数中的负数是( )A、 B、 C、 D、3. 我市某一周每天的最高气温统计如下(单位:℃):27,28,29,28,29,30,29.这组数据的众数与中位数分别是( ).A、28,28 B、28,29 C、29,28 D、29,294. 矩形的边长是 ,一条对角线的长是 ,则矩形的面积是( )A、 B、 C、 . D、5. 若 的两根分别是 与5,则多项式 可以分解为( )A、 B、 C、 D、6. 如图,四边形ABCD的对角线AC,BD相交于点O,且AB∥CD,添加下列条件后仍不能判断四边形ABCD是平行四边形的是( )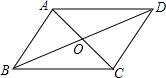 A、AB=CD B、AD∥BC C、OA=OC D、AD=BC7. 随着人民生活水平的提高,中国春节已经成为中国公民旅游黄金周.国家旅游局数据显示,2017年春节中国公民出境旅游约615万人次,2018,2019两年出境旅游人数持续增长,在2019年春节出境旅游达到700万人次,设2018年与2019年春节出境旅游总量较上一年春节的平均增长率为x,则下列方程正确的是( ).A、615(1+x)=700 B、615(1+2x)=700 C、 D、8. 如图,在六边形 中, , 分别平分 ,则 的度数为( )
A、AB=CD B、AD∥BC C、OA=OC D、AD=BC7. 随着人民生活水平的提高,中国春节已经成为中国公民旅游黄金周.国家旅游局数据显示,2017年春节中国公民出境旅游约615万人次,2018,2019两年出境旅游人数持续增长,在2019年春节出境旅游达到700万人次,设2018年与2019年春节出境旅游总量较上一年春节的平均增长率为x,则下列方程正确的是( ).A、615(1+x)=700 B、615(1+2x)=700 C、 D、8. 如图,在六边形 中, , 分别平分 ,则 的度数为( )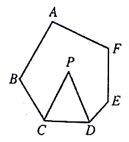 A、 B、 C、 D、9. 如图,将边长为 的正方形绕点B逆时针旋转30°,那么图中点M的坐标为( )
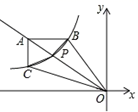
A、 B、 C、 D、9. 如图,将边长为 的正方形绕点B逆时针旋转30°,那么图中点M的坐标为( )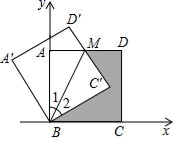 A、( ,1) B、(1, ) C、( , ) D、( , )10. 已知:如图在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线 ( x >0)经过D点,交AB于E点,且OB∙AC=160,则点E的坐标为( ).
A、( ,1) B、(1, ) C、( , ) D、( , )10. 已知:如图在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线 ( x >0)经过D点,交AB于E点,且OB∙AC=160,则点E的坐标为( ).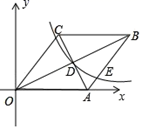 A、(3,8) B、(12, ) C、(4,8) D、(12,4)
A、(3,8) B、(12, ) C、(4,8) D、(12,4)二、填空题
-
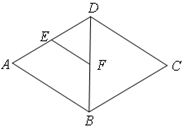
11. 计算: .12. 用反证法证明“等腰三角形的底角是锐角”时,首先应假设13. 如图,在菱形ABCD中,点E是AD的中点,对角线AC,BD交于点F,若菱形ABCD的周长是24,则EF=.
 14. 如果关于x的方程kx2﹣6x+9=0有两个相等的实数根,那么k的值为.15. 若 是李华同学在求一组数据的方差时,写出的计算过程,则其中的 =.16. 已知点A(a,b)是一次函数 的图象与反比例函数 的图象的一个交点,则 =.17. 如图,平行四边形ABCD的对角线AC,BD交于O,EF过点O与AD,BC分别交于E,F,若AB=4,BC=5,OE=1.5,则四边形EFCD的周长.
14. 如果关于x的方程kx2﹣6x+9=0有两个相等的实数根,那么k的值为.15. 若 是李华同学在求一组数据的方差时,写出的计算过程,则其中的 =.16. 已知点A(a,b)是一次函数 的图象与反比例函数 的图象的一个交点,则 =.17. 如图,平行四边形ABCD的对角线AC,BD交于O,EF过点O与AD,BC分别交于E,F,若AB=4,BC=5,OE=1.5,则四边形EFCD的周长.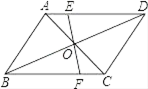 18. 如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y= (k≠0,x>0)的图象经过顶点C、D,若点C的横坐标为5,BE=3DE,则k的值为.
18. 如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y= (k≠0,x>0)的图象经过顶点C、D,若点C的横坐标为5,BE=3DE,则k的值为.
三、解答题
-
19.(1)、 - - ;(2)、20. 解方程:(1)、(2)、21. 如图,在四边形ABCD中,AC、BD相交于点O,O是AC的中点,AB//DC,AC=10,BD=8.
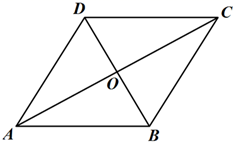 (1)、求证:四边形ABCD是平行四边形;(2)、若AC⊥BD,求平行四边形ABCD的面积.22. 某学校八年级开展英语拼写大赛,一班和二班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示:
(1)、求证:四边形ABCD是平行四边形;(2)、若AC⊥BD,求平行四边形ABCD的面积.22. 某学校八年级开展英语拼写大赛,一班和二班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示: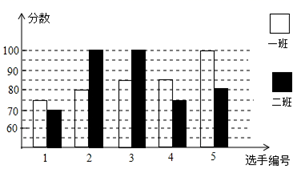 (1)、根据图示填写下表
(1)、根据图示填写下表班级
中位数(分)
众数(分)
平均数(分)
一班
85
二班
100
85
(2)、结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩比较好?(3)、已知一班的复赛成绩的方差是70,请求出二班复试成绩的方差,并说明哪个班成绩比较稳定?