浙江绍兴市越城区2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-06-15 类型:期末考试
一、选择题
-
1. 下列计算正确的是( )A、4 B、 C、2 = D、32. 下列各点中,在函数y=- 图象上的是( )A、 B、 C、 D、3. 一元二次方程 配方后可化为( )A、 B、 C、 D、4. 一个多边形的内角和比外角和的 倍多 ,则它的边数是( )A、八 B、九 C、十 D、十一5. 如图,在四边形 中,E是 边的中点,连接 并延长交 的延长线于点F,且 添加一个条件使四边形 是平行四边形,下面四个条件中可选择的是( )
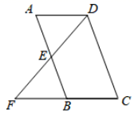 A、 B、 C、 D、6. 如图,点A在双曲线 上,点B在双曲线 , 轴,分别过点A,B向 轴作垂线,垂足分别为D,C.若矩形ABCD的面积是8,则k的值为( )
A、 B、 C、 D、6. 如图,点A在双曲线 上,点B在双曲线 , 轴,分别过点A,B向 轴作垂线,垂足分别为D,C.若矩形ABCD的面积是8,则k的值为( ) A、12 B、10 C、8 D、67. 甲、乙两人各射击6次,甲所中的环数是8,5,5,a,b,c,且甲所中的环数的平均数是6,众数是8;乙所中的环数的平均数是6,方差是4.根据以上数据,对甲,乙射击成绩的正确判断是( )A、甲射击成绩比乙稳定 B、乙射击成绩比甲稳定 C、甲,乙射击成绩稳定性相同 D、甲、乙射击成绩稳定性无法比较8. 如图,要在平行四边形 内作一个菱形.甲,乙两位同学的作法分别如下:
A、12 B、10 C、8 D、67. 甲、乙两人各射击6次,甲所中的环数是8,5,5,a,b,c,且甲所中的环数的平均数是6,众数是8;乙所中的环数的平均数是6,方差是4.根据以上数据,对甲,乙射击成绩的正确判断是( )A、甲射击成绩比乙稳定 B、乙射击成绩比甲稳定 C、甲,乙射击成绩稳定性相同 D、甲、乙射击成绩稳定性无法比较8. 如图,要在平行四边形 内作一个菱形.甲,乙两位同学的作法分别如下:
对于甲乙两人的作法,可判断( )
A、甲正确,乙错误 B、甲错误,乙正确 C、甲,乙均正确 D、甲、乙均错误9. 欧几里得的《原本》记载,形如 的方程的图解法是:画 ,使 , , ,再在斜边 上截取 .则该方程的一个正根是( )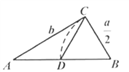 A、 的长 B、 的长 C、 的长 D、 的长10. 如图,在正方形 中, ,点 , 分别在 、 上, , , 相交于点 ,若图中阴影部分的面积与正方形 的面积之比为 ,则 的周长为( )
A、 的长 B、 的长 C、 的长 D、 的长10. 如图,在正方形 中, ,点 , 分别在 、 上, , , 相交于点 ,若图中阴影部分的面积与正方形 的面积之比为 ,则 的周长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如果一组数据的方差为9,那么这组数据的标准差是.12. 在▱ABCD中,如果∠A+∠C=140°,那么∠B=度.13. 已知关于x的一元二次方程mx2+5x+m2﹣2m=0有一个根为0,则m= .14. 如图,如果一次函数 与反比例函数 的图象交于 , 两点,那么不等式 的解为.
 15. 已知 是实数,且 和 都是整数,那么 的值是.16. 如图,Rt△ABC中,C= 90o , 以斜边AB为边向外作正方形 ABDE,且正方形对角线交于点D,连接OC,已知AC=5,OC=6 ,则另一直角边BC的长为.
15. 已知 是实数,且 和 都是整数,那么 的值是.16. 如图,Rt△ABC中,C= 90o , 以斜边AB为边向外作正方形 ABDE,且正方形对角线交于点D,连接OC,已知AC=5,OC=6 ,则另一直角边BC的长为.
三、解答题
-
17. 计算或化简:(1)、 ;(2)、18. 已知:关于 的方程 .(1)、求证:方程有两个不相等的实数根.(2)、若方程的一个根是 ,求另一个根及 值.19. 如图, 的对角线 , 相交于点 , 过点 且与 , 分别相交于点 , .求证: .
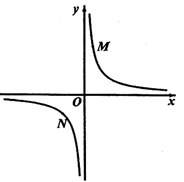
 20. 反比例函数 的图象如图所示, , 是该图象上的两点,
20. 反比例函数 的图象如图所示, , 是该图象上的两点,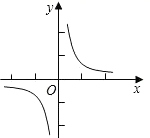 (1)、求m的取值范围;(2)、比较 与 的大小.21. 某地2015年为做好“精准扶贫”,投入资金1280万元用于异地安置,并规划投入资金逐年增加,2017年在2015年的基础上增加投入资金1600万元.(1)、从2015年到2017年,该地投入异地安置资金的年平均增长率为多少?(2)、在2017年异地安置的具体实施中,该地计划投入资金不低于500万元用于优先搬迁租房奖励,规定前1000户(含第1000户)每户每天奖励8元,1000户以后每户每天补助5元,按租房400天计算,试求今年该地至少有多少户享受到优先搬迁租房奖励?22.(1)、探究新知:如图1,已知 与 的面积相等,试判断 与 的位置关系,并说明理由.
(1)、求m的取值范围;(2)、比较 与 的大小.21. 某地2015年为做好“精准扶贫”,投入资金1280万元用于异地安置,并规划投入资金逐年增加,2017年在2015年的基础上增加投入资金1600万元.(1)、从2015年到2017年,该地投入异地安置资金的年平均增长率为多少?(2)、在2017年异地安置的具体实施中,该地计划投入资金不低于500万元用于优先搬迁租房奖励,规定前1000户(含第1000户)每户每天奖励8元,1000户以后每户每天补助5元,按租房400天计算,试求今年该地至少有多少户享受到优先搬迁租房奖励?22.(1)、探究新知:如图1,已知 与 的面积相等,试判断 与 的位置关系,并说明理由. (2)、结论应用:
(2)、结论应用:①如图2,点 , 在反比例函数 的图像上,过点 作 轴,过点 作 轴,垂足分别为 , ,连接 .试证明: .
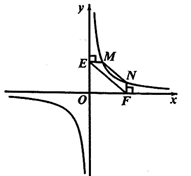
②若①中的其他条件不变,只改变点 , 的位置如图3所示,请画出图形,判断 与 的位置关系并说明理由.
 23. 在正方形 中,点P是直线 上一点.连接 ,将线段 绕点P顺时针旋转 ,得到线段 ,连接 .
23. 在正方形 中,点P是直线 上一点.连接 ,将线段 绕点P顺时针旋转 ,得到线段 ,连接 . (1)、如图1.若点P在线段CB的延长线上过点E作 于H.与对角线AC交于点F.
(1)、如图1.若点P在线段CB的延长线上过点E作 于H.与对角线AC交于点F.①请仔细阅读题目,根据题意在图上补全图形;②求证: .
(2)、若点P在射线 上,直接写出 , , 三条线段之间的数量关系(不必写过程).