陕西省延安市洛川县2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-06-15 类型:期末考试
一、选择题
-
1. 一个直角三角形斜边上的中线为5,斜边上的高为4,则此三角形的面积为( )A、25 B、16 C、20 D、102. 一个射手连续射靶10次,其中3次射中10环,3次射中9环,4次射中8环.则该射手射中环数的中位数和众数分别为( )A、8,9 B、9,8 C、8.5,8 D、8.5,93. 抛物线y=ax2+bx和直线y=ax+b在同一坐标系的图象可能是( )A、
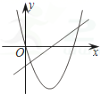 B、
B、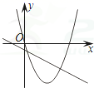 C、
C、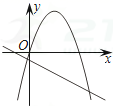 D、
D、 4. 矩形一个角的平分线分矩形一边为2cm和3cm两部分,则这个矩形的面积为( )A、10cm2 B、15cm2 C、12cm2 D、10cm2或15cm25. 某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1056张照片,如果全班有x名同学,根据题意,列出方程为( )A、x(x+1)=1056 B、x(x-1)=1056 C、x(x+1)=1056×2 D、x(x-1)=1056×26. 某商品降价 后欲恢复原价,则提价的百分数为( ).A、 B、 C、 D、7. 如图,将一个边长为4和8的长方形纸片ABCD折叠,使C点与A点重合,则折痕EF的长是( )
4. 矩形一个角的平分线分矩形一边为2cm和3cm两部分,则这个矩形的面积为( )A、10cm2 B、15cm2 C、12cm2 D、10cm2或15cm25. 某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1056张照片,如果全班有x名同学,根据题意,列出方程为( )A、x(x+1)=1056 B、x(x-1)=1056 C、x(x+1)=1056×2 D、x(x-1)=1056×26. 某商品降价 后欲恢复原价,则提价的百分数为( ).A、 B、 C、 D、7. 如图,将一个边长为4和8的长方形纸片ABCD折叠,使C点与A点重合,则折痕EF的长是( ) A、 B、 C、 D、8. 若y+1与x-2成正比例,当 时, ;则当 时, 的值是( )A、-2 B、-1 C、0 D、19. 关于函数y= -x-3的图象,有如下说法:
A、 B、 C、 D、8. 若y+1与x-2成正比例,当 时, ;则当 时, 的值是( )A、-2 B、-1 C、0 D、19. 关于函数y= -x-3的图象,有如下说法:①图象过点(0,-3);②图象与x轴的交点是(-3,0);③由图象可知y随x的增大而增大; ④图象不经过第一象限;⑤图象是与y= -x+4平行的直线.其中正确的说法有( )
A、5个 B、4个 C、3个 D、2个10. 已知直线y=kx-4(k<0)与两坐标轴所围成的三角形面积等于4,则该直线的表达式为( )A、y= -x-4 B、y= -2x-4 C、y= -3x+4 D、y= -3x-411. 已知二次函数y= 2x2+8x-1的图象上有点A(-2,y1),B(-5,y2),C(-1,y3),则y1、y2、y3的大小关系为( )A、 B、 C、 D、12. 已知二次函数y=ax2+bx+c (a≠0)的图象如图所示,则①abc>0,②b2-4ac>0,③2a+b>0,④a+b+c<0,这四个式子中正确的个数有( )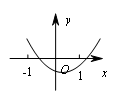 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
13. 一组数据1,2,a,4,5的平均数是3,则这组数据的方差为 .14. 关于x的一元二次方程(x+1)(x+7)= -5的根为.15. 如图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ,那么图中矩形AMKP的面积S1与矩形QCNK的面积S2的大小关系是S1S2;(填“>”或“<”或“=”)
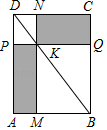 16. 关于x的方程(m﹣2)x2+2x+1=0有实数根,则偶数m的最大值为.17. 如图所示四个二次函数的图象中,分别对应的是①y=ax2;②y=bx2;③y=cx2;④y=dx2.则a、b、c、d的大小关系为.
16. 关于x的方程(m﹣2)x2+2x+1=0有实数根,则偶数m的最大值为.17. 如图所示四个二次函数的图象中,分别对应的是①y=ax2;②y=bx2;③y=cx2;④y=dx2.则a、b、c、d的大小关系为.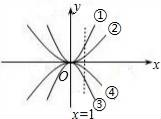 18. 已知菱形有一个锐角为60°,一条对角线长为4cm,则其面积为 cm2.19. 把二次函数y= -2x2-4x-1的图象向上平移3个单位长度,再向右平移4个单位长度,则两次平移后的图象的解析式是 ;20. 如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△AED;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CDE;⑤S△ABE=S△CEF . 其中正确的是 .
18. 已知菱形有一个锐角为60°,一条对角线长为4cm,则其面积为 cm2.19. 把二次函数y= -2x2-4x-1的图象向上平移3个单位长度,再向右平移4个单位长度,则两次平移后的图象的解析式是 ;20. 如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△AED;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CDE;⑤S△ABE=S△CEF . 其中正确的是 .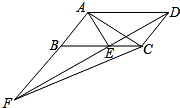
三、解答题
-
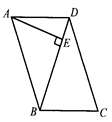
21. 如图,在平行四边形 中, , 于点 ,试求 的度数.
 22. 某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的测试成绩如下表所示:
22. 某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的测试成绩如下表所示:
根据录用程序,组织200名职工对三人利用投票推荐的方式进行民主评议,三人得票率(没有弃权票,每位职工只能推荐1人)如扇形图所示,每得一票记作1分.
(1)、如果根据三项测试的平均成绩确定录用人选,那么谁将被录用(精确到 0.01 )?(2)、根据实际需要,单位将笔试、面试、民主评议三项测试得分按5 : 2 : 3的比例确定个人成绩,那么谁将被录用?23. 如图,一次函数y= -3x+6的图象与 轴、 轴分别交于 、 两点. (1)、将直线 向左平移1个单位长度,求平移后直线的函数关系式;(2)、求出平移过程中,直线 在第一象限扫过的图形的面积.24. 如图,点 是ΔABC内一点,连接OB、OC,并将AB、OB、OC、AC的中点 、 、 、 依次连结,得到四边形 .
(1)、将直线 向左平移1个单位长度,求平移后直线的函数关系式;(2)、求出平移过程中,直线 在第一象限扫过的图形的面积.24. 如图,点 是ΔABC内一点,连接OB、OC,并将AB、OB、OC、AC的中点 、 、 、 依次连结,得到四边形 . (1)、求证:四边形 是平行四边形;(2)、若 为 的中点,OM=5,∠OBC与∠OCB互余,求DG的长度.25. 邻居张老汉养了一群鸡,现在要建一长方形鸡场,鸡场的一边靠墙(墙长18米),墙对面有一个2米宽的门,另三边(门除外)用竹篱笆围成,篱笆总长34米.请同学解决以下问题:
(1)、求证:四边形 是平行四边形;(2)、若 为 的中点,OM=5,∠OBC与∠OCB互余,求DG的长度.25. 邻居张老汉养了一群鸡,现在要建一长方形鸡场,鸡场的一边靠墙(墙长18米),墙对面有一个2米宽的门,另三边(门除外)用竹篱笆围成,篱笆总长34米.请同学解决以下问题: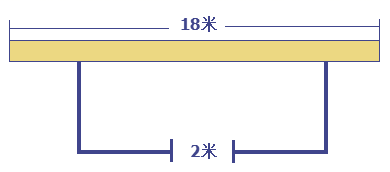 (1)、若设鸡场的面积为y平方米,鸡场与墙平行的一边长为x米,请写出y与x之间的函数关系式,并写出x的取值范围;(2)、当鸡场的面积为160平方米时,鸡场的长与宽分别是多少米?(3)、鸡场的最大面积是多少?并求出此时鸡场的长与宽分别是多少米?26. 如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与 轴交于 点.
(1)、若设鸡场的面积为y平方米,鸡场与墙平行的一边长为x米,请写出y与x之间的函数关系式,并写出x的取值范围;(2)、当鸡场的面积为160平方米时,鸡场的长与宽分别是多少米?(3)、鸡场的最大面积是多少?并求出此时鸡场的长与宽分别是多少米?26. 如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与 轴交于 点.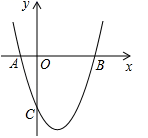 (1)、求该抛物线的解析式;(2)、P是y轴正半轴上一点,且△PAB是以AB为腰的等腰三角形,试求点P的坐标;(3)、作直线BC,若点Q是直线BC下方抛物线上的一动点,三角形QBC面积是否有最大值,若有,请求出此时Q点的坐标;若没有,请说明理由.
(1)、求该抛物线的解析式;(2)、P是y轴正半轴上一点,且△PAB是以AB为腰的等腰三角形,试求点P的坐标;(3)、作直线BC,若点Q是直线BC下方抛物线上的一动点,三角形QBC面积是否有最大值,若有,请求出此时Q点的坐标;若没有,请说明理由.