陕西省咸阳市兴平市2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-06-15 类型:期末考试
一、选择题
-
1. 已知 ,下列不等式中正确是( )A、 B、 C、 D、2. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、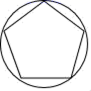 C、
C、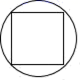 D、
D、 3. 分式 有意义的条件是( )A、 B、 C、 D、4. 经过多边形一个角的两边剪掉这个角,则得到的新多边形的外角和( )A、比原多边形多 B、比原多边形少 C、与原多边形外角和相等 D、不确定5. 若分式 □ 的运算结果为x(x≠0),则在“口”中添加的运算符号为( )A、+ B、﹣ C、+或÷ D、﹣或×6. 下列因式分解正确的是( )A、2x2﹣6x=2x(x﹣6) B、﹣a3+ab=﹣a (a2﹣b) C、﹣x2﹣y2=﹣(x+y)(x﹣y) D、m2﹣9n2=(m+9n)(m﹣9n)7. 把一些笔记本分给几个学生,如果每人分3本,那么余8本,如果每人分5本,则最后一个人分到的本数不足3本,则共有学生( )人.A、4 B、5 C、6 D、5或68. 已知四边形 ,对角线 与 交于点O,从下列条件中:① ;② ;③ ;④ .任取其中两个,以下组合能够判定四边形 是平行四边形的是( )A、①② B、②③ C、②④ D、①④9. 如果关于x的分式方程 有增根,则增根的值为( )A、0 B、-1 C、0或-1 D、不存在10. 如图, ABCD中,点E在边 上,以 为折痕,将 向上翻折,点B正好落在边 上的点F处,若 的周长为8, 的周长为18,则 的长为( )
3. 分式 有意义的条件是( )A、 B、 C、 D、4. 经过多边形一个角的两边剪掉这个角,则得到的新多边形的外角和( )A、比原多边形多 B、比原多边形少 C、与原多边形外角和相等 D、不确定5. 若分式 □ 的运算结果为x(x≠0),则在“口”中添加的运算符号为( )A、+ B、﹣ C、+或÷ D、﹣或×6. 下列因式分解正确的是( )A、2x2﹣6x=2x(x﹣6) B、﹣a3+ab=﹣a (a2﹣b) C、﹣x2﹣y2=﹣(x+y)(x﹣y) D、m2﹣9n2=(m+9n)(m﹣9n)7. 把一些笔记本分给几个学生,如果每人分3本,那么余8本,如果每人分5本,则最后一个人分到的本数不足3本,则共有学生( )人.A、4 B、5 C、6 D、5或68. 已知四边形 ,对角线 与 交于点O,从下列条件中:① ;② ;③ ;④ .任取其中两个,以下组合能够判定四边形 是平行四边形的是( )A、①② B、②③ C、②④ D、①④9. 如果关于x的分式方程 有增根,则增根的值为( )A、0 B、-1 C、0或-1 D、不存在10. 如图, ABCD中,点E在边 上,以 为折痕,将 向上翻折,点B正好落在边 上的点F处,若 的周长为8, 的周长为18,则 的长为( ) A、5 B、8 C、7 D、6
A、5 B、8 C、7 D、6二、填空题
-
11. 分式 的值为0,那么x的值为.12. 多项式 因式分解后有一个因式为 ,则k的值为.13. 如图,一次函数 与 的图象相交于点 ,则关于x的不等式 的解集是.
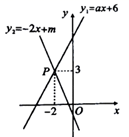 14. 如图,在 中, 平分 , ,垂足为点D,交 于点G,E为 的中点,连结 , , ,则 的长为 .
14. 如图,在 中, 平分 , ,垂足为点D,交 于点G,E为 的中点,连结 , , ,则 的长为 .
三、解答题
-
15. 分解因式:(1)、(2)、16. 解不等式组: ,并把解集在数轴上表示出来.17. 解分式方程: .18. 先化简,再求值: ,其中 .19. 如图,根据要求画图.

①把 向右平移5个方格,画出平移的图形.
②以点B为旋转中心,把 顺时针方向旋转 ,画出旋转后的图形.
20. 用圆规、直尺作图,不写作法,但要保留作图痕迹.已知:四边形ABCD
求作:点P,使∠PBC=∠PCB,且点P到AD和DC的距离相等.
 21. 如图,在等腰 中, ,D为底边BC延长线上任意一点,过点D作 ,与AC延长线交于点E.
21. 如图,在等腰 中, ,D为底边BC延长线上任意一点,过点D作 ,与AC延长线交于点E. (1)、则 的形状是;(2)、若在AC上截取 ,连接FB、FD,判断FB、FD的数量关系,并给出证明.22. 某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵10元,用350元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.(1)、求甲、乙两种商品每件的价格各是多少元?(2)、计划购买这两种商品共50件,且投入的经费不超过3200元,那么最多购买多少件甲种商品?23. 如图,平行四边形 中, ,点 、 分别在 、 的延长线上, , ,垂足为点 , .
(1)、则 的形状是;(2)、若在AC上截取 ,连接FB、FD,判断FB、FD的数量关系,并给出证明.22. 某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵10元,用350元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.(1)、求甲、乙两种商品每件的价格各是多少元?(2)、计划购买这两种商品共50件,且投入的经费不超过3200元,那么最多购买多少件甲种商品?23. 如图,平行四边形 中, ,点 、 分别在 、 的延长线上, , ,垂足为点 , . (1)、求证: 是 中点;(2)、求 的长.24. 如图,四边形 是面积为 的平行四边形,其中 .
(1)、求证: 是 中点;(2)、求 的长.24. 如图,四边形 是面积为 的平行四边形,其中 . (1)、如图①,点 为 边上任意一点,则 的面积 和 的面积 之和与 的面积 之间的数量关系是;(2)、如图②,设 交于点 ,则 的面积 和 的面积 之和与 的面积 之间的数量关系是;(3)、如图③,点 为 内任意一点时,试猜想 的面积 和 的面积 之和与 的面积 之间的数量关系,并加以证明;(4)、如图④,已知点 为 内任意一点, 的面积为 , 的面积为 ,连接 ,求 的面积.
(1)、如图①,点 为 边上任意一点,则 的面积 和 的面积 之和与 的面积 之间的数量关系是;(2)、如图②,设 交于点 ,则 的面积 和 的面积 之和与 的面积 之间的数量关系是;(3)、如图③,点 为 内任意一点时,试猜想 的面积 和 的面积 之和与 的面积 之间的数量关系,并加以证明;(4)、如图④,已知点 为 内任意一点, 的面积为 , 的面积为 ,连接 ,求 的面积.