陕西省咸阳市三原县2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-06-15 类型:期末考试
一、选择题
-
1. 下列平面图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 分式方程 的解为( )A、 B、 C、 D、3. 如图, 两地被池塘隔开,小明先在直线 外选一点C,然后测量出 , 的中点 ,并测出 的长为 .由此,他可以知道A、B间的距离为( )
2. 分式方程 的解为( )A、 B、 C、 D、3. 如图, 两地被池塘隔开,小明先在直线 外选一点C,然后测量出 , 的中点 ,并测出 的长为 .由此,他可以知道A、B间的距离为( ) A、 B、 C、 D、4. 如果一个正多边形的内角和是这个正多边形外角和的2倍,那么这个正多边形是( )A、等边三角形 B、正四边形 C、正六边形 D、正八边形5. 不等式5x﹣2>3(x+1)的最小整数解为( )A、3 B、2 C、1 D、﹣26. 已知 是完全平方式,则m的值为( )A、2 B、4 C、 D、7. 如图,在▱ABCD中, , 的平分线与DC交于点E, ,BF与AD的延长线交于点F,则BC等于( )
A、 B、 C、 D、4. 如果一个正多边形的内角和是这个正多边形外角和的2倍,那么这个正多边形是( )A、等边三角形 B、正四边形 C、正六边形 D、正八边形5. 不等式5x﹣2>3(x+1)的最小整数解为( )A、3 B、2 C、1 D、﹣26. 已知 是完全平方式,则m的值为( )A、2 B、4 C、 D、7. 如图,在▱ABCD中, , 的平分线与DC交于点E, ,BF与AD的延长线交于点F,则BC等于( ) A、2 B、 C、3 D、8. 如图,在 中, , , 是角平分线, ,垂足为点E.若 ,则 的长是( )
A、2 B、 C、3 D、8. 如图,在 中, , , 是角平分线, ,垂足为点E.若 ,则 的长是( ) A、 B、 C、 D、59. 一个无人超市仓库的货物搬运工作全部由机器人A和机器人B完成,工作记录显示机器人A比机器人B每小时多搬运50件货物.机器人A搬运2000件货物与机器人B搬运1600件货物所用的时间相等,则机器人A每小时搬运货物( )A、250件 B、200件 C、150件 D、100件10. 如图,在 中, , , ,延长 到点E,使 ,交 于点F,在 上取一点G,使 ,连接 .有以下结论:① 平分 ;② ;③ 是等边三角形;④ ,则正确的结论有( )
A、 B、 C、 D、59. 一个无人超市仓库的货物搬运工作全部由机器人A和机器人B完成,工作记录显示机器人A比机器人B每小时多搬运50件货物.机器人A搬运2000件货物与机器人B搬运1600件货物所用的时间相等,则机器人A每小时搬运货物( )A、250件 B、200件 C、150件 D、100件10. 如图,在 中, , , ,延长 到点E,使 ,交 于点F,在 上取一点G,使 ,连接 .有以下结论:① 平分 ;② ;③ 是等边三角形;④ ,则正确的结论有( )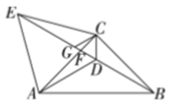 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 若代数式 在实数范围内有意义,则实数x的取值范围是.12. 因式分解: .13. 如图,已知一次函数 与一次函数 的图像相交于点P(-2,1),则关于不等式x+b≥mx-n的解集为.
 14. 如图,在平行四边形 中,连接 ,且 ,过点 作 于点 ,过点 作 于点 ,在 的延长线上取一点 , ,若 ,则 的度数为 .
14. 如图,在平行四边形 中,连接 ,且 ,过点 作 于点 ,过点 作 于点 ,在 的延长线上取一点 , ,若 ,则 的度数为 .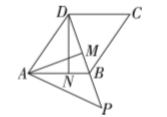
三、解答题
-
15. 化简: .16. 如图,已知直线 和 上一点 ,用尺规作 的垂线,使它经过点 .(保留作图痕迹,不写作法)
 17. 解不等式组: ,并把解集在数轴上表示出来.
17. 解不等式组: ,并把解集在数轴上表示出来.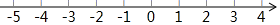 18. 如图,四边形ABCD是平行四边形,分别以AB,CD为边向外作等边△ABE和△CDF,连接AF,CE.求证:四边形AECF为平行四边形.
18. 如图,四边形ABCD是平行四边形,分别以AB,CD为边向外作等边△ABE和△CDF,连接AF,CE.求证:四边形AECF为平行四边形. 19. 如图,已知 各顶点的坐标分别为 , , .
19. 如图,已知 各顶点的坐标分别为 , , .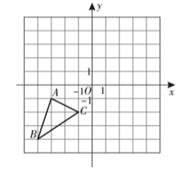 (1)、画出 以点 为旋转中心,按逆时针方向旋转 后得到的 ;
(1)、画出 以点 为旋转中心,按逆时针方向旋转 后得到的 ;和平移距离.
(2)、将 先向右平移4个单位长度,再向上平移5个单位长度,得到 .①在图中画出 ;
②如果将 看成是由 经过一次平移得到的,请指出这一平移的平移方向和平移距离.
20. 阅读材料,回答问题:材料:将一个多项式分组后,可提公因式或运用公式继续分解的方法是因式分解中的分组分解法,一般的分组分解法有四种形式,即“ ”分法、“ ”分法、“ ”分法及“ ”分法等.
如“ ”分法:
请你仿照以上方法,探索并解决下列问题:
分解因式:
(1)、 ;(2)、 .21. 如图,四边形ABCD的对角线AC⊥BD于点E,AB=BC,F为四边形ABCD外一点,且∠FCA=90°,∠CBF=∠DCB. (1)、求证:四边形DBFC是平行四边形;(2)、如果BC平分∠DBF,∠CDB=45°,BD=2,求AC的长.22. 某商店计划购进甲、乙两种商品,乙种商品的进价是甲种商品进价的九折,用3600元购买乙种商品要比购买甲种商品多买10件.(1)、求甲、乙两种商品的进价各是多少元?(2)、该商店计划购进甲、乙两种商品共80件,且乙种商品的数量不低于甲种商品数量的3倍.甲种商品的售价定为每件80元,乙种商品的售价定为每件70元,若甲、乙两种商品都能卖完,求该商店能获得的最大利润.
(1)、求证:四边形DBFC是平行四边形;(2)、如果BC平分∠DBF,∠CDB=45°,BD=2,求AC的长.22. 某商店计划购进甲、乙两种商品,乙种商品的进价是甲种商品进价的九折,用3600元购买乙种商品要比购买甲种商品多买10件.(1)、求甲、乙两种商品的进价各是多少元?(2)、该商店计划购进甲、乙两种商品共80件,且乙种商品的数量不低于甲种商品数量的3倍.甲种商品的售价定为每件80元,乙种商品的售价定为每件70元,若甲、乙两种商品都能卖完,求该商店能获得的最大利润.