陕西省商南县2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2020-06-15 类型：期末考试

进入出卷网下载

一、选择题

1. 下列根式中属于最简二次根式的是（）

A、 $\sqrt{a^{2} + 1}$ B、 $\sqrt{8}$ C、 $\frac{1}{\sqrt{3}}$ D、 $\sqrt{0.5}$

查看试题解析
2. 下列各组数据中，不是勾股数的是（）

A、3，4，5 B、5，7，9 C、8，15，17 D、7，24，25

查看试题解析
3. 抚顺市中小学机器人科技大赛中，有7名学生参加决赛，他们决赛的成绩各不相同，其中一名参赛选手想知道自己能否进入前4名，他除了知道自己成绩外还要知道这7名学生成绩的（）

A、中位数 B、众数 C、平均数 D、方差

查看试题解析
4. 下列计算正确的是（）

A、 $\sqrt{5} - \sqrt{2} = \sqrt{3}$ B、 $\sqrt{6} \div \sqrt{2} = \sqrt{3}$ C、 $2 \sqrt{2} \times 3 \sqrt{2} = 6 \sqrt{2}$ D、 $(\sqrt{2} + 1) (\sqrt{2} - 1) = 3$

查看试题解析
5. 如图， $A$ 、 $B$ 两处被池塘隔开，为了测量 $A$ 、 $B$ 两处的距离，在 $A B$ 外选一点 $C$ ，连接 $A C$ 、 $B C$ ，并分别取线段 $A C$ 、 $B C$ 的中点 $E$ 、 $F$ ，测得 $E F = 15 m$ ，则 $A B$ 的长为（）

A、 $7.5 m$ B、 $15 m$ C、 $30 m$ D、 $45 m$

查看试题解析
6. 甲、乙、丙、丁四人进行射击测试，每人10次射击成绩平均数均是9.2环，方差分别为S_甲²=0.56，S_乙²=0.60，S_丙²=0.50，S_丁²=0.45，则成绩最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
7. 如图，在矩形AOBC中，A（–2，0），B（0，1）．若正比例函数y=kx的图象经过点C，则k的值为（）

A、– $\frac{1}{2}$ B、 $\frac{1}{2}$ C、–2 D、2

查看试题解析
8. 如图， $Δ A B C$ 中， $C D$ 是 $A B$ 边上的高，若 $A B = 1.5$ ， $B C = 0.9$ ， $A C = 1.2$ ，则 $C D$ 的长为（）

A、0.72 B、1.125 C、2 D、不能确定

查看试题解析
9. 如图，在正方形ABCD外侧，作等边三角形ADE，AC，BE相交于点F，则∠BFC为（）

A、75° B、60° C、55° D、45°

查看试题解析
10. 已知 $A (x_{1}, y_{1})$ ， $B (x_{2}, y_{2})$ ，是一次函数 $y = (a - 3) x + 5$ 图象上不同的两个点，若 $(x_{1} - x_{2}) (y_{1} - y_{2}) < 0$ ，则a的取值范围是（）

A、 $a > 0$ B、 $a < 0$ C、 $a > 3$ D、 $a < 3$

查看试题解析

二、填空题

11. 已知 $a$ ， $b$ 为实数，且满足 $\sqrt{a - 8} + \sqrt{8 - a} = b - 2$ ，则 $\sqrt{a b} =$ .

查看试题解析
12. 某射击小组有20人，教练根据他们某次射击的数据绘制成如图所示的统计图，则这组数据的中位数是.

查看试题解析
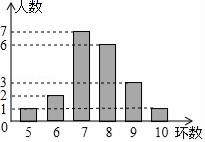13. 若一次函数y=（2m﹣1）x+3﹣2m的图象经过一、二、四象限，则m的取值范围是

查看试题解析
14. 一种圆柱形口杯（厚度忽略不计），测得内部底面半径为 $2.5 c m$ ，高为 $12 c m$ .吸管如图放进杯里，杯口外面露出部分长为 $4 c m$ ，则吸管 $A D$ 的长度为 $c m$ .

查看试题解析
15. 如图， $▱ A B C D$ 的对角线 $A C$ 、 $B D$ 相交于点O， $E F$ 经过点O，分别交 $A D$ 、 $B C$ 于点E、F，已知 $▱ A B C D$ 的面积是 $20 c m^{2}$ ，则图中阴影部分的面积是.

查看试题解析
16. 已知直线y=2x+4与x轴、y轴分别交于A、B两点，点P（-1，m）为平面直角坐标系内一动点，若△ABP面积为1，则m的值为.

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{48} \div \sqrt{3} - \sqrt{\frac{1}{2}} \times \sqrt{12} + \sqrt{24}$

(2)、已知 $x = \sqrt{3} + 1$ ， $y = \sqrt{3} - 1$ ，求 $x^{2} + y^{2}$ 的值.

查看试题解析
18. 某工厂车间为了了解工人日均生产能力的情况，随机抽取10名工人进行测试，将获得数据制成如下统计图.

(1)、求这10名工人的日均生产件数的平均数、众数、中位数；

(2)、若日均生产件数不低于12件为优秀等级，该工厂车间共有工人120人，估计日均生产能力为“优秀”等级的工人约为多少人？

查看试题解析
19. 如图，四边形ABCD是平行四边形，E、F是对角线AC上的两点，且AE＝CF，顺次连接B、E、D，F.求证：四边形BEDF是平行四边形.

查看试题解析
20. “五一节”期间，申老师一家自驾游去了离家170千米的某地，下面是他们离家的距离y（千米）与汽车行驶时间x（小时）之间的函数图象．

(1)、求他们出发半小时时，离家多少千米？

(2)、求出AB段图象的函数表达式；

(3)、他们出发2小时时，离目的地还有多少千米？

查看试题解析
21. 如图，在矩形 $A B C D$ 中，对角线 $A C$ 、 $B D$ 交于点 $O$ ，且过点 $B$ 作 $B E / / A C$ ，过点 $C$ 作 $C E / / B D$ ，两直线相交于点 $E$ .

(1)、求证：四边形 $B O C E$ 是菱形；

(2)、若 $B E = A B = 1$ ，求矩形 $A B C D$ 的面积.

查看试题解析
22. 勾股定理是几何学中的明珠，它充满魅力，在现实世界中有着广泛的应用.请你尝试应用勾股定理解决下列问题：一架 $2.6 m$ 长的梯子 $A B$ 斜靠在一竖直的墙 $A O$ 上，这时 $A O$ 为 $2.4 m$ ，如果梯子的顶端 $A$ 沿墙下滑 $0.5 m$ ，那么梯子底端 $B$ 向外移了多少米？（注意： $\sqrt{3.15} \approx 1.77$ ）

查看试题解析
23. 在进行二次根式运算时，我们有时会碰上如 $\frac{2}{\sqrt{3} + 1}$ 这样的式子，我们还可以将其进一步化简： $\frac{2}{\sqrt{3} + 1} = \frac{2 \times (\sqrt{3} - 1)}{(\sqrt{3} + 1) (\sqrt{3} - 1)} = \frac{2 \times (\sqrt{3} - 1)}{2} = \sqrt{3} - 1$ 以上这种化简过程叫做分母有理化. $\frac{2}{\sqrt{3} + 1}$ 还可以尝试用以下方法化简：
$\frac{2}{\sqrt{3} + 1} = \frac{3 - 1}{\sqrt{3} + 1} = \frac{{(\sqrt{3})}^{2} - 1^{2}}{\sqrt{3} + 1} = \frac{(\sqrt{3} + 1) (\sqrt{3} - 1)}{\sqrt{3} + 1} = \sqrt{3} - 1$

(1)、请用两种不同的方法化简； $\frac{2}{\sqrt{11} + 3}$

(2)、请任选一种方法化简： $\frac{3}{\sqrt{11} - 2 \sqrt{2}} - \frac{4}{\sqrt{15} - \sqrt{11}}$

查看试题解析
24. 正方形 $A B C D$ 的对角线相交于点O，点O又是正方形 $A_{1} B_{1} C_{1} O$ 的一个顶点，而且这两个正方形的边长相等.试证明：无论正方形 $A_{1} B_{1} C_{1} O$ 绕点O怎样转动，两个正方形重叠部分的面积，总等于一个正方形面积的 $\frac{1}{4}$ .

查看试题解析
25. 暑假期间，商洛剧院举行专场音乐会，成人票每张20元，学生票每张5元，为了吸引广大师生来听音乐会，剧院制定了两种优惠方案：
方案一：购买一张成人票赠送一张学生票；

方案二：成人票和学生票都打九折.

我校现有4名老师与若干名（不少于4人）学生听音乐会.

(1)、设学生人数为 $x$ （人），付款总金额为 $y$ （元），请分别确定两种优惠方案中 $y$ 与 $x$ 的函数关系式；

(2)、请你结合参加听音乐会的学生人数，计算说明怎样购票花费少？

查看试题解析