陕西省城固县2018-2019学年八年级下学期数学期末考试试卷a

试卷更新日期：2020-06-15 类型：期末考试

进入出卷网下载

一、选择题

1. 下列汽车标志中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若分式 $\frac{x}{x + 4}$ 有意义，则实数x的取值范围是（）

A、 $x \neq 0$ B、 $x = 0$ C、 $x \neq - 4$ D、 $x \neq 4$

查看试题解析
3. 不等式 $\frac{x + 1}{2} > \frac{2 x + 1}{3} - 1$ 的正整数解的个数是（）

A、7个 B、6个 C、4个 D、0个

查看试题解析
4. 如图，在四边形ABCD中，点D在AC的垂直平分线上， $A B ∥ C D$ .若 $∠ B A C = 25^{°}$ ，则 $∠ A D C$ 的度数是（）

A、 $130^{°}$ B、 $120^{°}$ C、 $100^{°}$ D、50°

查看试题解析
5. 若关于x的分式方程 $\frac{x - 6}{x - 5} + 1 = \frac{k}{5 - x}$ 有增根，则k的值是（）

A、 $- 1$ B、 $- 2$ C、2 D、1

查看试题解析
6.
如图，在Rt△ABC中，∠ACB =90°，∠ABC=30°，将△ABC绕点C顺时针旋转 $α$ 角（0°< $α$ <180°）至△A′B′C ，使得点A′恰好落在AB边上，则 $α$ 等于（）.

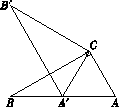A、150° B、90° C、60° D、30°

查看试题解析
7. 如图，AD、BE分别是 $△ A B C$ 的中线和角平分线， $A D ⊥ B E$ ， $A D = B E = 4$ ，F为CE的中点，连接DF，则AF的长等于（）

A、2 B、3 C、 $\sqrt{5}$ D、 $2 \sqrt{5}$

查看试题解析
8. 如图，在 $Rt △ A B C$ 中， $∠ B A C = 90^{°}$ ， $∠ A C B = 30^{°}$ ， $A B = 2$ ，将△ABC沿直线BC向右平移得到△DEF，连接AD，若AD=2，则点C到DF的距离为（）

A、1 B、2 C、2.5 D、4

查看试题解析
9. 为打击毒品犯罪，我县缉毒警察乘警车，对同时从县城乘汽车出发到A地的两名毒犯实行抓捕，警车比汽车提前15分钟到A地，A地距离县城8千米，警车的平均速度是汽车平均速度的2.5倍，若设汽车的平均速度是每小时x千米，根据题意可列方程为（）

A、 $\frac{8}{x}$ +15＝ $\frac{8}{2.5 x}$ B、 $\frac{8}{x}$ ＝ $\frac{8}{2.5 x}$ +15 C、 $\frac{8}{x} + \frac{1}{4}$ ＝ $\frac{8}{2.5 x}$ D、 $\frac{8}{x}$ ＝ $\frac{8}{2.5 x}$ $+ \frac{1}{4}$

查看试题解析
10. 如图，已知△ABC是边长为3的等边三角形，点D是边BC上的一点，且BD＝1，以AD为边作等边△ADE，过点E作EF∥BC，交AC于点F，连接BF，则下列结论中①△ABD≌△BCF；②四边形BDEF是平行四边形；③S_{四边形BDEF}＝ $\frac{\sqrt{3}}{2}$ ；④S_△_AEF＝ $\sqrt{3}$ .其中正确的有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 已知某个正多边形的每个内角都是 $120^{°}$ ，这个正多边形的内角和为.

查看试题解析
12. 如果多项式 $x^{2} + (2 - k) x y + 9 y^{2}$ 是一个完全平方式，那么k的值为.

查看试题解析
13. 在一次“人与环境”知识竞赛中，共有25个题，每题四个答案，其中只有一个答案正确，每选对一题得4分，不选或选错倒扣2分，如果一个学生在本次竞赛中得分不低于60分，那么他至少要答对题．

查看试题解析
14. 如图，平行四边形ABCD中，点O是对角线AC的中点，点E在边AB上，连接DE，取DE的中点F，连接EO并延长交CD于点G.若BE=3CG，OF=2，则线段AE的长是.

查看试题解析

三、解答题

15. 解方程： $\frac{1 - x}{x - 2} = \frac{x}{2 x - 4} - 1$ .

查看试题解析
16. 解不等式组： ${\begin{array}{l} 2 x + 9 \geq 3 \\ \frac{1 + 2 x}{3} > x - 1 \end{array}$

查看试题解析
17. 如图，已知直线l和l外一点P，用尺规作l的垂线，使它经过点P.（保留作图痕迹，不写作法）

查看试题解析
18. 如图，在一块半径为R的圆形板材上，冲去半径为r的四个小圆，小刚测得R=6.8cm，r=1.6cm，请利用因式分解求出剩余阴影部分的面积（结果保留π）

查看试题解析
19. 先化简，再求值： $(1 + \frac{1}{x^{2} - 1}) \div \frac{x^{2}}{x^{2} - 2 x + 1}$ ，其中 $x = 2$ .

查看试题解析
20. 如图，在 $△ A B C$ 中， $A B = A C$ ，点M、N分别在BC所在的直线上，且BM=CN，求证：△AMN是等腰三角形.

查看试题解析
21. 如图，已知 $△ A B C$ 各顶点的坐标分别为 $A (- 3 ， - 4)$ ， $B (- 1 ， - 3)$ ， $C (- 4 ， - 1)$ .

(1)、画出 $△ A B C$ 以点B为旋转中心，按顺时针方向旋转 $90^{°}$ 后得到的 $△ A_{1} B C_{1}$ ；

(2)、将 $△ A B C$ 先向右平移5个单位长度，再向上平移3个单位长度，得到 $△ A_{2} B_{2} C_{2}$ .
①在图中画出 $△ A_{2} B_{2} C_{2}$ ，并写出点A的对应点 $A_{2}$ 的坐标；

②如果将 $△ A_{2} B_{2} C_{2}$ 看成是由 $△ A B C$ 经过一次平移得到的，请指出这一平移的平移方向和平移距离.

查看试题解析
22. 如图，四边形ABCD为平行四边形， $∠ B A D$ 的平分线AE交CD于点F交BC的延长线于点E.

(1)、求证： $B E = C D$ ；

(2)、连接BF、AC、DE，当 $B F ⊥ A E$ 时，求证：四边形ACED是平行四边形.

查看试题解析
23. 问题背景：对于形如 $x^{2} - 120 x + 3600$ 这样的二次三项式，可以直接用完全平方公式将它分解成 ${(x - 60)}^{2}$ ，对于二次三项式 $x^{2} - 120 x + 3456$ ，就不能直接用完全平方公式分解因式了．此时常采用将 $x^{2} - 120 x$ 加上一项 $60^{2}$ ，使它与 $x^{2} - 120 x$ 的和成为一个完全平方式，再减去 $60^{2}$ ，整个式子的值不变，于是有：
$x^{2} - 120 + 3456$ = $x^{2} - 2 \times 60 x + 60^{2} - 60^{2} + 3456$
= ${(x - 60)}^{2} - 144$ = ${(x - 60)}^{2} - 12^{2}$ = $(x - 60 + 12) (x - 60 - 12)$ = $(x - 48) (x - 72)$
问题解决：

(1)、请你按照上面的方法分解因式： $x^{2} - 140 x + 4756$ ；

(2)、已知一个长方形的面积为 $a^{2} + 8 a b + 12 b^{2}$ ，长为 $a + 2 b$ ，求这个长方形的宽．

查看试题解析
24. 某校为了改善办公条件，计划从厂家购买A、B两种型号电脑。已知每台A种型号电脑价格比每台B种型号电脑价格多0.1万元，且用10万元购买A种型号电脑的数量与用8万元购买B种型号电脑的数量相同.

(1)、求A、B两种型号电脑每台价格各为多少万元？

(2)、学校预计用不多于9.2万元的资金购进这两种电脑共20台，则最多可购买A种型号电脑多少台？

查看试题解析
25. 在 ▱ ABCD中，∠ADC的平分线交直线BC于点E、交AB的延长线于点F，连接AC.

(1)、如图1，若∠ADC=90°，G是EF的中点，连接AG、CG.
①求证：BE=BF；

②请判断△AGC的形状，并说明理由.

(2)、如图2，若∠ADC=60°，将线段FB绕点F顺时针旋转60°至FG，连接AG、CG，判断△AGC的形状.（直接写出结论不必证明）

查看试题解析