陕西省宝鸡市岐山县2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2020-06-15 类型：期末考试

进入出卷网下载

一、选择题

1. 下列图形中，既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如果分式 $\frac{2 x}{x + 5}$ 有意义，那么 $x$ 的取值范围是（）

A、 $x \neq 0$ B、 $x \leq - 5$ C、 $x \geq - 5$ D、 $x \neq - 5$

查看试题解析
3. 下列式子从左边到右边的变形是因式分解的是（）

A、 $6 a^{2} b^{2} = 3 a b \cdot 2 a b$ B、 $x^{2} - 4 x + 4 = {(x - 2)}^{2}$ C、 $(x + 1) (x - 1) = x^{2} - 1$ D、 $x^{2} - x - 2 = x (x - 1) - 2$

查看试题解析
4. 一个关于x的一元一次不等式组的解集在数轴上的表示如图，则该不等式组的解集是（）

A、x＞1 B、x≥1 C、x＞3 D、x≥3

查看试题解析
5. 下列分式是最简分式的是（）

A、 $- \frac{12 b}{27 a^{2}}$ B、 $\frac{x^{2} + y^{2}}{x + y}$ C、 $\frac{a^{2} + a b}{b^{2} + a b}$ D、 $\frac{x + y}{x^{2} - y^{2}}$

查看试题解析
6. 解关于 $x$ 的方程 $\frac{x - 6}{x - 5} + 1 = \frac{m}{x - 5}$ （其中m为常数）产生增根，则常数m的值等于（）

A、-2 B、2 C、-1 D、1

查看试题解析
7. 如图，在Rt△ABC中，∠C=90°，∠ABC=30°，AB=8，将△ABC沿CB方向向右平移得到△DEF.若四边形ABED的面积为8，则平移距离为（）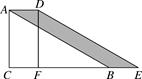

A、2 B、4 C、8 D、16

查看试题解析
8. 如图，∠1、∠2、∠3、∠4、∠5是五边形ABCDE的外角，且∠1=∠2=∠3=∠4=70°，则∠AED的度数是（）

A、110° B、108° C、105° D、100°

查看试题解析
9. 如图，AB＝AC，BE⊥AC于点E，CF⊥AB于点F，BE，CF交于点D，则下列结论中不正确的是（）

A、△ABE≌△ACF B、点D在∠BAC的平分线上 C、△BDF≌△CDE D、D是BE的中点

查看试题解析
10. 某园林队原计划由6名工人对180平方米的区域进行绿化,由于施工时增加了2名工人,结果比原计划提前3小时完成任务,若每人每小时绿化的面积相同，求每人每小时绿化的面积。若设每人每小时绿化的面积为 $x$ 平方米，根据题意下面所列方程正确的是（）

A、 $\frac{180}{6 x} - \frac{180}{(6 + 2) x} = 3$ B、 $\frac{180}{(6 + 2) x} - \frac{180}{6 x} = 3$ C、 $\frac{180}{(6 - 3) x} - \frac{180}{6 x} = 2$ D、 $\frac{180}{(6 + 2) x} + \frac{180}{6 x} = 3$

查看试题解析

二、填空题

11. 当x＝时，分式 $\frac{x^{2} - 4}{x + 2}$ 的值为0.

查看试题解析
12. 如图，已知 $Δ A B C$ 中， $A B = A C$ ， $A D$ 平分 $∠ B A C$ ，点 $E$ 是 $A B$ 的中点，若 $A C = 6$ ，则 $D E$ 的长为。

查看试题解析
13.
如图，在平行四边形ABCD中，对角线AC与BD相交于点O，BD⊥AD，AD=6，AB=10，则△AOB的面积为

查看试题解析
14. 某次数学竞赛共有20道选择题，评分标准为对1题给5分，错1题扣3分，不答题不给分也不扣分，小华有3题未做，则他至少答对道题，总分才不会低于65分.

查看试题解析
15. 分解因式：

(1)、 $a x^{2} - a y^{2}$ ；

(2)、 $x (x^{2} - x y) - (4 x^{2} - 4 x y)$ 。

查看试题解析
16. 当x为何值时，分式 $\frac{2 x}{x - 1}$ 的值比分式 $\frac{1}{x^{2} - 1}$ 的值大2？

查看试题解析
17. 先化简： $(\frac{3}{a + 1} - a + 1) \div \frac{a^{2} - 4 a + 4}{a + 1}$ ，然后给a选择一个你喜欢的数代入求值。

查看试题解析
18. 已知：如图，在 $Δ A B C$ 中， $A B = A C ， ∠ B = 36 °$ 。

(1)、尺规作图：作线段 $A B$ 的垂直平分线交 $B C$ 于点 $D$ ，垂足为点 $F$ ，连接 $A D$ ；（保留作图痕迹，不写作法）；

(2)、求证： $Δ A C D$ 是等腰三角形。

查看试题解析
19. 如图，在Rt△ABC中，∠ACB＝90°，点D、E分别在AB、AC上，且CE＝BC ，连接CD ，将线段CD绕点C按顺时针方向旋转90°后得到CF ，连接EF ．

(1)、求证：△BDC≌△EFC；

(2)、若EF∥CD ，求证：∠BDC＝90°．

查看试题解析
20. 如图，在 $▱ A B C D$ 中，点 $E ， F$ 对角线 $A C$ 上，且 $A E = C F$ ，连接 $D E 、 E B 、 B F 、 F D$ 。

求证：

(1)、 $Δ A D E ≅ Δ C B F$ ；

(2)、四边形 $D E B F$ 是平行四边形。

查看试题解析
21. $△ A B C$ 的中线BD，CE相交于O，F，G分别是BO，CO的中点，求证： $E F / / D G$ ，且 $E F = D G$ .

查看试题解析
22. 如图，已知 $Δ A B C$ 是等边三角形，点D在 $B C$ 边上， $Δ A D F$ 是以 $A D$ 为边的等边三角形，过点F作 $B C$ 的平行线交线段 $A C$ 于点E，连接 $B F$ 。

求证：

(1)、 $Δ A F B ≅ Δ A D C$ ；

(2)、四边形 $B C E F$ 是平行四边形.

查看试题解析
23. 某校为美化校园，计划对面积为1800m²的区域进行绿化，安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍，并且在独立完成面积为400 m²区域的绿化时，甲队比乙队少用4天.

(1)、求甲、乙两工程队每天能完成绿化的面积分别是多少m²？

(2)、若学校每天需付给甲队的绿化费用是0.4万元，乙队为0.25万元，要使这次的绿化总费用不超过8万元，至少应安排甲队工作多少天？

查看试题解析