陕西省宝鸡市麟游县2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2020-06-15 类型：期末考试

进入出卷网下载

一、选择题

1. 二次根式 $\sqrt{\frac{1}{3}}$ 、 $\sqrt{12}$ 、 $\sqrt{30}$ 、 $\sqrt{x + 2}$ 、 $\sqrt{5 x^{2}}$ 、 $\sqrt{x^{2} + y^{2}}$ 中，最简二次根式有（）个.

A、1 个 B、2 个 C、3 个 D、4个

查看试题解析
2. 若式子 $\frac{\sqrt{2 - x}}{x - 2}$ 有意义，则x的取值范围为（）.

A、x≥2 B、x≠2 C、x≤2 D、x＜2

查看试题解析
3. 如果下列各组数是三角形的三边，那么不能组成直角三角形的一组数是（）

A、7，24，25 B、 $3 \frac{1}{2}$ ， $4 \frac{1}{2}$ ， $5 \frac{1}{2}$ C、6，8，10 D、9，12，15

查看试题解析
4. 在四边形ABCD中，O是对角线的交点，能判定这个四边形是正方形的条件是（）

A、AC=BD，AB∥CD，AB=CD B、AD∥BC，∠A=∠C C、AO=BO=CO=DO，AC⊥BD D、AO=CO，BO=DO，AB=BC

查看试题解析
5. 如图，在平行四边形ABCD中，∠B＝70°，AE平分∠BAD交BC于点E，CF∥AE交AD于点F，则∠1＝（）

A、45° B、55° C、50° D、60°

查看试题解析
6. 下列图形中，表示一次函数y＝mx+n与正比例函数y＝mnx（m，n为常数，且mn≠0）的图象的是（）

A、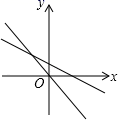 B、 C、 D、

查看试题解析
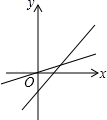7. 如图所示，函数 $y_{1} = | x |$ 和 $y_{2} = \frac{1}{3} x + \frac{4}{3}$ 的图象相交于（–1，1），（2，2）两点.当 $y_{1} > y_{2}$ 时，x的取值范围是（）

A、x<–1 B、x<–1或x>2 C、x>2 D、–1<x<2

查看试题解析
8. 在方差公式 $S^{2} = \frac{1}{n} [{(x_{1} - \bar{x})}^{2} + {(x_{2} - \bar{x})}^{2} + \dots + {(x_{n} - \bar{x})}^{2}]$ 中，下列说法不正确的是（）

A、n是样本的容量 B、 $x_{n}$ 是样本个体 C、 $\bar{x}$ 是样本平均数 D、S是样本方差

查看试题解析
9. 多多班长统计去年1～8月“书香校园”活动中全班同学的课外阅读数量（单位：本），绘制了如图折线统计图，下列说法正确的是（）

A、极差是47 B、众数是42 C、中位数是58 D、每月阅读数量超过40的有4个月

查看试题解析
10. 如图，在 $Δ A B C$ 中， $A B = 3$ ， $A C = 4$ ， $B C = 5$ ， $P$ 为边 $B C$ 上一动点， $P E ⊥ A B$ 于点 $E$ ， $P F ⊥ A C$ 于点 $F ， M$ 为 $E F$ 的中点，则 $A M$ 的最小值为（）

A、 $\frac{5}{4}$ B、 $\frac{5}{2}$ C、 $\frac{5}{3}$ D、 $\frac{6}{5}$

查看试题解析

二、填空题

11. 函数 $y = \frac{\sqrt{3 - x}}{x + 2}$ 的自变量x的取值范围是．

查看试题解析
12. 四边形ABCD中，AD∥BC，AD=BC，对角线AC、BD相交于点O，若CD＝3cm，△BOC的周长比△AOB的周长大2cm，则四边形ABCD的周长＝cm.

查看试题解析
13. 某一次函数的图象经过点（3， $- 1$ ），且函数y随x的增大而增大，请你写出一个符合条件的函数解析式

查看试题解析
14. 马拉松赛选手分甲、乙两组运动员进行了艰苦的训练，他们在相同条件下各10次比赛，成绩的平均数相同，方差分别为0.25，0.21，则成绩较为稳定的是（选填“甲”或“乙）

查看试题解析
15. 在直角三角形ABC中，∠B=90°，BD是AC边上的中线，∠A=30°，AB=5 $\sqrt{3}$ ，则△ADB的周长为

查看试题解析

三、解答题

16. 计算

(1)、 $9 \sqrt{3} + 7 \sqrt{12} - 5 \sqrt{48} + 2 \sqrt{\frac{1}{3}}$

(2)、 $(2 \sqrt{5} - 5 \sqrt{2}) (2 \sqrt{5} + 5 \sqrt{2}) - {(\sqrt{5} - \sqrt{2})}^{2}$

查看试题解析
17. 先化简，再求值：当a=7时，求a+ $\sqrt{1- 2 a + a^{2}}$ 的值.

查看试题解析
18. 在△ABC中，∠C=30°，AC=4cm，AB=3cm，求BC的长.

查看试题解析
19. 如图，在直角梯形ABCD中，AD∥BC，∠B=90°，AG∥CD交BC于点G，点E、F分别为AG、CD的中点，连接DE、FG．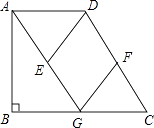

(1)、求证：四边形DEGF是平行四边形；

(2)、当点G是BC的中点时，求证：四边形DEGF是菱形．

查看试题解析
20. a，b分别是7- $\sqrt{5}$ 的整数部分和小数部分.

(1)、分别写出a，b的值；

(2)、求 $2 a^{2} -b$ 的值

查看试题解析
21. 小颖和小亮上山游玩，小颖乘缆车，小亮步行，两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍，小颖在小亮出发后50 min才乘上缆车，缆车的平均速度为180 m/min.设小亮出发x min后行走的路程为y m.图中的折线表示小亮在整个行走过程中y与x的函数关系.

(1)、小亮行走的总路程是cm，他途中休息了min.

(2)、①当50≤x≤80时，求y与x的函数关系式；
②当小颖到达缆车终点为时，小亮离缆车终点的路程是多少？

查看试题解析

22. 为了从甲、乙两名选手中选拔出一个人参加射击比赛，现对他们进行一次测验，两个人在相同条件下各射靶10次，为了比较两人的成绩，制作了如下统计图表.

甲、乙射击成绩统计表

平均数（环）	中位数（环）	方差	命中10环的次数
甲	7		0
乙			1

甲、乙射击成绩折线统计图

(1)、请补全上述图表（请直接在表中填空和补全折线图）；

(2)、如果规定成绩较稳定者胜出，你认为谁应胜出？说明你的理由；

(3)、如果希望（2）中的另一名选手胜出，根据图表中的信息，应该制定怎样的评判规则？为什么？

查看试题解析

23. 如图，直线y=kx+6分别与x轴、y轴交于点E，F，已知点E的坐标为（﹣8，0），点A的坐标为（﹣6，0）.

(1)、求k的值；

(2)、若点P（x，y）是该直线上的一个动点，且在第二象限内运动，试写出△OPA的面积S关于x的函数解析式，并写出自变量x的取值范围.

(3)、探究：当点P运动到什么位置时，△OPA的面积为 $\frac{27}{8}$ ，并说明理由.

查看试题解析