陕西省宝鸡市凤翔县2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2020-06-15 类型：期末考试

进入出卷网下载

一、选择题

1. 不等式 $2 x + 5 > 0$ 的解集是（）

A、 $x < \frac{5}{2}$ B、 $x > \frac{5}{2}$ C、 $x > - \frac{5}{2}$ D、 $x < - \frac{5}{2}$

查看试题解析
2. 下列多项式能用完全平方公式进行分解因式的是（）

A、 $x^{2} + 1$ B、 $x^{2} + 2 x + 4$ C、 $x^{2} - 2 x + 1$ D、 $x^{2} + x + 1$

查看试题解析
3. 若分式 $\frac{| x | - 1}{x + 1}$ 的值为0，则（）

A、 $x = \pm 1$ B、 $x = 1$ C、 $x = - 1$ D、 $x = 0$

查看试题解析
4. 下面的两个三角形一定全等的是（）

A、腰相等的两个等腰三角形 B、一个角对应相等的两个等腰三角形 C、斜边对应相等的两个直角三角形 D、底边相等的两个等腰直角三角形

查看试题解析
5. 如图，已知直线 $y_{1} = a x + b$ 与 $y_{2} = m x + n$ 相交于点 $A$ （2， $- 1$ ），若 $y_{1} > y_{2}$ ，则 $x$ 的取值范围是（）

A、 $x < 2$ B、 $x > 2$ C、 $x < - 1$ D、 $x > - 1$

查看试题解析
6. 在 $Δ A B C$ 中，D、E分别是 $B C$ 、 $A C$ 边的中点，若 $D E = 3$ ，则 $A B$ 的长是（）

A、9 B、5 C、6 D、4

查看试题解析
7. 如图，四边形ABCD中，AB＝CD，对角线AC，BD交于点O，下列条件中不能说明四边形ABCD是平行四边形的是（）

A、AD＝BC B、AC＝BD C、AB∥CD D、∠BAC＝∠DCA

查看试题解析
8. 解关于x的方程 $\frac{x - 3}{x - 1} = \frac{m}{x - 1}$ 产生增根，则常数m的值等于（）

A、-2 B、-1 C、1 D、2

查看试题解析
9. 如图，在△ABC中，∠CAB＝75°，在同一平面内，将△ABC绕点A逆时针旋转到△AB′C′的位置，使得CC′∥AB，则∠CAC′为（）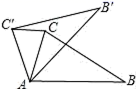

A、30° B、35° C、40° D、50°

查看试题解析
10. 已知点A（0，0），B（0，4），C（3，t+4），D（3，t）. 记N（t）为▱ABCD内部（不含边界）整点的个数，其中整点是指横坐标和纵坐标都是整数的点，则N（t）所有可能的值为( )

A、6、7 B、7、8 C、6、7、8 D、6、8、9

查看试题解析

二、填空题

11. 因式分解： $2 a^{2} - 4 a =$ .

查看试题解析
12. 若一个多边形的内角和为1080°，则这个多边形的边数为.

查看试题解析
13. 已知 $\frac{a - 3 b}{2 a + b} = 3$ ，则 $\frac{6 b - 2 a}{6 a + 3 b} =$ .

查看试题解析
14. 如图所示，为估计池塘两岸边 $A$ ， $B$ 两点间的距离，在池塘的一侧选取点 $C$ ，分别取 $C A$ 、 $C B$ 的中点 $E$ ， $F$ ，测的 $E F = 18 m$ ，则 $A$ ， $B$ 两点间的距离是 $m$ .

查看试题解析

三、解答题

15.

(1)、解不等式组 ${\begin{matrix} 2 x + 3 > 1 \\ x - 2 \leq \frac{1}{2} (x + 2) \end{matrix}$

(2)、解方程： $\frac{x - 2}{x + 2} - 1 = \frac{3}{x^{2} - 4}$ .

查看试题解析
16. 先化简，再求值： $\frac{m^{2} - 2 m + 1}{m^{2} - 1}$ ÷（m﹣1﹣ $\frac{m - 1}{m + 1}$ ），其中m＝ $\sqrt{3}$ .

查看试题解析
17. 如图，在平面直角坐标系中， $Rt Δ ABC$ 的三个顶点分别是 $A (- 4 ， 2)$ 、 $B (0 ， 4)$ 、 $C (0 ， 2)$ .

(1)、画出 $Δ A B C$ 关于点C成中心对称的△ $A_{1} B_{1} C$ ；平移 $Δ A B C$ ，若点A的对应点 $A_{2}$ 的坐标为 $(0 ， - 4)$ ，画出平移后对应的△ $A_{2} B_{2} C_{2}$ ；

(2)、△ $A_{1} B_{1} C$ 和△ $A_{2} B_{2} C_{2}$ 关于某一点成中心对称，则对称中心的坐标为.

查看试题解析
18. 已知：线段 $a$ 、 $c$ .

求作： $R t Δ A B C$ ，使 $B C = a$ ， $A B = c$ ， $∠ A = 90 °$

查看试题解析
19. 某商场计划购进A、B两种新型节能台灯，已知B型节能台灯每盏进价比A型的多40元，且用3000元购进的A型节能台灯与用5000元购进的B型节能台灯的数量相同.

(1)、求每盏A型节能台灯的进价是多少元？

(2)、商场将购进A、B两型节能台灯100盏进行销售，A型节能台灯每盏的售价为90元，B型节能台灯每盏的售价为140元，且B型节能台灯的进货数量不超过A型节能台灯数量的2倍.应怎样进货才能使商场在销售完这批台灯时利最多？此时利润是多少元？

查看试题解析
20. 如图，在△ABC中，∠C=90∘，AC=BC，AD平分∠CAB，DE⊥AB，垂足为E.

(1)、求证：CD=BE；

(2)、若AB=10，求BD的长度。

查看试题解析
21.

(1)、如图1所示，在 $▱ A B C D$ 中，E为边 $C D$ 上一点，将 $Δ A D E$ 沿 $A E$ 折叠至 $Δ A D^{'} E$ 处， $A D^{'}$ 与 $C E$ 交于点F.若 $∠ B = 52 °$ ， $∠ D A E = 20 °$ ，则 $∠ F E D^{'}$ 的大小为.

(2)、提出命题：如图2，在四边形 $A B C D$ 中， $∠ A = ∠ C$ ， $∠ A B C = ∠ A D C$ ，求证：四边形 $A B C D$ 是平行四边形.
小明提供了如下解答过程：

证明：连接 $B D$ .

∵ $∠ 1 + ∠ 3 = 180 ° - ∠ A$ ， $∠ 2 + ∠ 4 = 180 ° - ∠ C$ ， $∠ A = ∠ C$ ，

∴ $∠ 1 + ∠ 3 = ∠ 2 + ∠ 4$ .

∵ $∠ A B C = ∠ A D C$ ，

∴ $∠ 1 = ∠ 4$ ， $∠ 2 = ∠ 3$ .

∴ $A B / / C D$ ， $A D / / B C$ .

∴四边形 $A B C D$ 是平行四边形（两组对边分别平行的四边形是平行四边形）.

反思交流：

①请问小明的解法正确吗？如果有错，说明错在何处，并给出正确的证明过程.

②用语言叙述上述命题：▲.

(3)、运用探究：
下列条件中，能确定四边形 $A B C D$ 是平行四边形的是（）

A、 $∠ A ： ∠ B ： ∠ C ： ∠ D = 1 ： 2 ： 3 ： 4$ B、 $∠ A ： ∠ B ： ∠ C ： ∠ D = 1 ： 3 ： 1 ： 3$ C、 $∠ A ： ∠ B ： ∠ C ： ∠ D = 2 ： 3 ： 3 ： 2$ D、 $∠ A ： ∠ B ： ∠ C ： ∠ D = 1 ： 1 ： 3 ： 3$

查看试题解析