广西南宁市西乡塘区2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-06-15 类型:期末考试
一、选择题
-
1. 若式子 在实数范围内有意义,则x的取值范围是( )A、x≥3 B、x≤3 C、x>3 D、x<32. 下列二次概式中,最简二次根式是( )A、 B、 C、 D、3. 下列各组数据中,能构成直角三角形的三边边长的是( )A、l,2,3 B、6,8,10 C、2,3,4 D、9,13,174. 甲,乙,丙,丁四人进行射击测试,记录每人10次射击成情,得到各人的射击成绩方差如表中所示,则成绩最稳定的是( )
统计量
甲
乙
丙
丁
方差
0.60
0.62
0.50
0.44
A、甲 B、乙 C、丙 D、丁5. 将一次函数y=4x的图象向上平移3个单位长度,得到图象对应的函数解析式为( )A、y=4x-3 B、y=2x-6 C、y=4x+3 D、y=-x-36.如图,在菱形ABCD中,AB=5,∠BCD=120°,则△ABC的周长等于( )
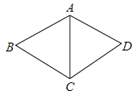 A、20 B、15 C、10 D、57. 一次函数 的图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 下列计算正确的是( )A、 × = B、 + = C、 D、 - =9. 某中学规定学生的学期体育成绩满分为100分,其中课外锻炼占20%,期中考试成绩占40%,期末考试成绩占40%。小乐的三项成绩(百分制)依次为95,90,85,则小彤这学期的体育成绩为是( )A、85 B、89 C、90 D、9510. 如图,在平行四边形ABCD中,用直尺和圆规作的∠BAD平分线交BC于点E,若AE=8,AB=5,则BF的长为( )
A、20 B、15 C、10 D、57. 一次函数 的图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 下列计算正确的是( )A、 × = B、 + = C、 D、 - =9. 某中学规定学生的学期体育成绩满分为100分,其中课外锻炼占20%,期中考试成绩占40%,期末考试成绩占40%。小乐的三项成绩(百分制)依次为95,90,85,则小彤这学期的体育成绩为是( )A、85 B、89 C、90 D、9510. 如图,在平行四边形ABCD中,用直尺和圆规作的∠BAD平分线交BC于点E,若AE=8,AB=5,则BF的长为( ) A、4 B、5 C、6 D、811. 打开某洗衣机开关,在洗涤衣服时(洗衣机内无水),洗衣机经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间满足某种函数关系,其函数图象大致为( )A、
A、4 B、5 C、6 D、811. 打开某洗衣机开关,在洗涤衣服时(洗衣机内无水),洗衣机经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间满足某种函数关系,其函数图象大致为( )A、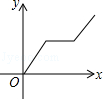 B、
B、 C、
C、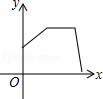 D、
D、 12. 如图,在平行四边形ABCD中,F,G分别为CD,AD的中点,BF=2,BG=3, ,则BC的长度为( )
12. 如图,在平行四边形ABCD中,F,G分别为CD,AD的中点,BF=2,BG=3, ,则BC的长度为( ) A、 B、 C、2.5 D、
A、 B、 C、2.5 D、二、填空题
-
13. 计算: =.14. 已知点M(m,3)在直线 上,则m=.15. 已知一组数据1,2,0,-1,x,1的平均数是1,则这组数据的极差为.16. 平行四边形ABCD中,若 , =.17. 如图,一次函数 与 的图的交点坐标为(2,3),则关于 的不等式 的解集为.
 18. 如图,菱形ABCD的对角线长分别为a、b,以菱形ABCD各边的中点为顶点作矩形 ,然后再以矩形 的中点为顶点作菱形 ,……,如此下去,得到四边形A2019B2019C2019D2019的面积用含a,b的代数式表示为.
18. 如图,菱形ABCD的对角线长分别为a、b,以菱形ABCD各边的中点为顶点作矩形 ,然后再以矩形 的中点为顶点作菱形 ,……,如此下去,得到四边形A2019B2019C2019D2019的面积用含a,b的代数式表示为.
三、解答题
-
19. 计算:20. 先化简,再求值: ,其中 .21. 为了进一步了解某校八年级学生的身体素质情况,体育老师对该校八年级(1)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,图表如下所示:
组别
次数x
频数(人数)
第1组
80≤x<100
6
第2组
100≤x<120
8
第3组
120≤x<140
a
第4组
140≤x<160
18
第5组
160≤x<180
6

请结合图表完成下列问题:
(1)、求表中a的值并把频数分布直方图补充完整;(2)、该班学生跳绳的中位数落在第组,众数落在第组;(3)、若在一分钟内跳绳次数少于120次的为测试不合格,则该校八年级共1000人中,一分钟跳绳 不合格的人数大约有多少?22. 已知一次函数y=2x和y=-x+4. (1)、在平面直角坐标中作出这两函数的函数图象(不需要列表);(2)、直线 垂直于 轴,垂足为点P(3,0).若这两个函数图象与直线 分别交于点A,B.求AB的长.23. 如图,在矩形ABCD中AD=12,AB=9,E为AD的中点,G是DC上一点,连接BE,BG,GE,并延长GE交BA的延长线于点F,GC=5
(1)、在平面直角坐标中作出这两函数的函数图象(不需要列表);(2)、直线 垂直于 轴,垂足为点P(3,0).若这两个函数图象与直线 分别交于点A,B.求AB的长.23. 如图,在矩形ABCD中AD=12,AB=9,E为AD的中点,G是DC上一点,连接BE,BG,GE,并延长GE交BA的延长线于点F,GC=5 (1)、求BG的长度;(2)、求证: 是直角三角形(3)、求证:24. 某社区计划对面积为1200m2的区域进行绿化.经投标,由甲、乙两个工程队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天.(1)、甲、乙两施工队每天分别能完成绿化的面积是多少?(2)、设先由甲队施工x天,再由乙队施工y天,刚好完成绿化任务,求y与x的函数解析式;(3)、在(2)的情况下,若甲队绿化费用为1600元/天,乙队绿化费用为700元/天,在施工过程中每天需要支付高温补贴a元(100≤a≤300),且工期不得超过14天,则如何安排甲,乙两队施工的天数,使施工费用最少?25. 如图1,BD是正方形ABCD的对角线,BC=4,点H是AD边上的一动点,连接CH,作 ,使得HE=CH,连接AE。
(1)、求BG的长度;(2)、求证: 是直角三角形(3)、求证:24. 某社区计划对面积为1200m2的区域进行绿化.经投标,由甲、乙两个工程队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天.(1)、甲、乙两施工队每天分别能完成绿化的面积是多少?(2)、设先由甲队施工x天,再由乙队施工y天,刚好完成绿化任务,求y与x的函数解析式;(3)、在(2)的情况下,若甲队绿化费用为1600元/天,乙队绿化费用为700元/天,在施工过程中每天需要支付高温补贴a元(100≤a≤300),且工期不得超过14天,则如何安排甲,乙两队施工的天数,使施工费用最少?25. 如图1,BD是正方形ABCD的对角线,BC=4,点H是AD边上的一动点,连接CH,作 ,使得HE=CH,连接AE。
 (1)、求证: ;(2)、如图2,过点E作EF//AD交对角线BD于点F,试探究:在点H的运动过程中,EF的长度是否为一个定值;如果是,请求出EF的长度。
(1)、求证: ;(2)、如图2,过点E作EF//AD交对角线BD于点F,试探究:在点H的运动过程中,EF的长度是否为一个定值;如果是,请求出EF的长度。