广西桂平市2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-06-15 类型:期末考试
一、选择题
-
1. 点 关于y轴对称的点的坐标是( )A、 B、 C、 D、2. 在下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、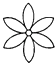 D、
D、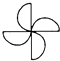 3. 下列几组数中,不能作为直角三角形三条边长的是( )A、3,4,5 B、5,12,13 C、7,24,25 D、9,39,404. 如图,在 中, , ,则 的度数是( )
3. 下列几组数中,不能作为直角三角形三条边长的是( )A、3,4,5 B、5,12,13 C、7,24,25 D、9,39,404. 如图,在 中, , ,则 的度数是( ) A、 B、 C、 D、5. 平南县某小区5月份随机抽取了15户家庭,对其用电情况进行了统计,统计情况如下(单位:度):78,62,95,108,87,103,99,74,87,105,88,76,76,94,79.则用电量在71~80的家庭有( )A、4户 B、5户 C、6户 D、7户6. 生物刘老师对本班50名学生的血型进行了统计,列出如下统计表.则本班O型血的有( )
A、 B、 C、 D、5. 平南县某小区5月份随机抽取了15户家庭,对其用电情况进行了统计,统计情况如下(单位:度):78,62,95,108,87,103,99,74,87,105,88,76,76,94,79.则用电量在71~80的家庭有( )A、4户 B、5户 C、6户 D、7户6. 生物刘老师对本班50名学生的血型进行了统计,列出如下统计表.则本班O型血的有( )血型
A型
B型
AB型
O型
频率
0.34
0.3
0.26
0.1
A、17人 B、15人 C、13人 D、5人7. 汽车由贵港驶往相距约350千米的桂林,如果汽车的平均速度是100千米/时,那么汽车距桂林的路程s(千米)与行驶时间t(小时)的函数关系可用图象表示为( )A、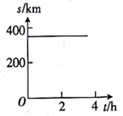 B、
B、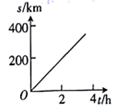 C、
C、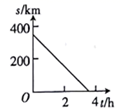 D、
D、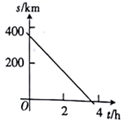 8. 如图在 中,D,E分别是AB、AC的中点若 的周长为16,则 的周长为( )
8. 如图在 中,D,E分别是AB、AC的中点若 的周长为16,则 的周长为( )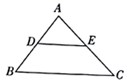 A、6 B、7 C、8 D、99. 如图,在 中, ,AD平分 , , ,那么点D到直线AB的距离是( )A、2cm B、4cm C、6cm D、10cm10. 将点 先向下平移4个单位长度,再向右平移3个单位长度后得到点Q,则点Q的坐标是( )A、 B、 C、 D、11. 我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A、B,把正方形沿箭头方向推,使点D落在y轴的正半轴上的点 处,则点C的对应点 的坐标为( )
A、6 B、7 C、8 D、99. 如图,在 中, ,AD平分 , , ,那么点D到直线AB的距离是( )A、2cm B、4cm C、6cm D、10cm10. 将点 先向下平移4个单位长度,再向右平移3个单位长度后得到点Q,则点Q的坐标是( )A、 B、 C、 D、11. 我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A、B,把正方形沿箭头方向推,使点D落在y轴的正半轴上的点 处,则点C的对应点 的坐标为( )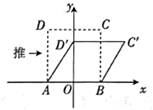 A、 B、 C、 D、12. 小军自制的匀速直线运动遥控车模型甲、乙两车同时分别从 、 出发,沿直线轨道同时到达 处,已知乙的速度是甲的速度的1.5倍,甲、乙两遥控车与 处的距离 、 (米)与时间 (分钟)的函数关系如图所示,则下列结论中:① 的距离为120米;②乙的速度为60米/分;③ 的值为 ;④若甲、乙两遥控车的距离不少于10米时,两车信号不会产生互相干扰,则两车信号不会产生互相干扰的 的取值范围是 ,其中正确的有( )个
A、 B、 C、 D、12. 小军自制的匀速直线运动遥控车模型甲、乙两车同时分别从 、 出发,沿直线轨道同时到达 处,已知乙的速度是甲的速度的1.5倍,甲、乙两遥控车与 处的距离 、 (米)与时间 (分钟)的函数关系如图所示,则下列结论中:① 的距离为120米;②乙的速度为60米/分;③ 的值为 ;④若甲、乙两遥控车的距离不少于10米时,两车信号不会产生互相干扰,则两车信号不会产生互相干扰的 的取值范围是 ,其中正确的有( )个 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 若n边形的每个内角都是 ,则 .14. 已知一个直角三角形的斜边长为6cm,那么这个直角三角形斜边上的中线长为cm.15. 在某次数学测验中,班长将全班50名同学的成绩(得分为整数)绘制成频数分布直方图(如图),从左到右的小长方形高的比为0.6:2:4:2.2:1.2,则得分在70.5到80.5之间的人数为.
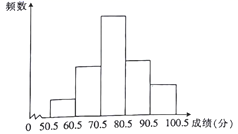 16. 在平面直角坐标系中,点 在第象限.17. 已知点 , 关于x轴对称,则 .18. 如图,在边长为2的正方形ABCD的外部作 ,且 ,连接DE、BF、BD,则 .
16. 在平面直角坐标系中,点 在第象限.17. 已知点 , 关于x轴对称,则 .18. 如图,在边长为2的正方形ABCD的外部作 ,且 ,连接DE、BF、BD,则 .
三、解答题
-
19. 如图,在平面直角坐标系xOy中,点 ,点 ,点 .
 (1)、①作出 关于y轴的对称图形 ;
(1)、①作出 关于y轴的对称图形 ;②写出点 、 、 的坐标
(2)、已知点 ,点 在直线 的图象上,求 的函数解析式.20. 如图,已知 和线段a,求作菱形ABCD,使 , .(只保留作图痕迹,不要求写出作法)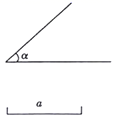 21. 已知一次函数 .(1)、若这个函数的图象经过原点,求a的值.(2)、若这个函数的图象经过一、三、四象限,求a的取值范围.22. 今年5月19日为第29个“全国助残日”我市某中学组织了献爱心捐款活动,该校数学课外活动小组对本次捐款活动做了一次抽样调查,并绘制了如下不完整的频数分布表和频数分布直方图(每组含前一个边界,不含后一个边界).
21. 已知一次函数 .(1)、若这个函数的图象经过原点,求a的值.(2)、若这个函数的图象经过一、三、四象限,求a的取值范围.22. 今年5月19日为第29个“全国助残日”我市某中学组织了献爱心捐款活动,该校数学课外活动小组对本次捐款活动做了一次抽样调查,并绘制了如下不完整的频数分布表和频数分布直方图(每组含前一个边界,不含后一个边界).捐款额(元)
频数
百分比
3
7.5%
7
17.5%
a
b
10
25%
6
15%
总计
100%
(1)、填空: , .(2)、补全频数分布直方图.(3)、该校有2000名学生估计这次活动中爱心捐款额在 的学生人数.23. 如图,点A在 的边ON上, 于点B, , 于点E, , 于点C.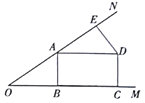
求证:四边形ABCD是矩形.
24. 端午节假期,某商场开展促销活动,活动规定:若购买不超过100元的商品,则按全额交费;若购买超过100元的商品,则超过100元的部分按8折交费.设商品全额为x元,交费为y元.(1)、写出y与x之间的函数关系式.(2)、某顾客在一次消费中,向售货员交纳了300元,那么在这次消费中,该顾客购买的商品全额为多少元?25. 在综合与实践课上,老师组织同学们以“矩形纸片的折叠”为主题开展数学活动. (1)、奋进小组用图1中的矩形纸片ABCD,按照如图2所示的方式,将矩形纸片沿对角线AC折叠,使点B落在点 处,则 与 重合部分的三角形的类型是.(2)、勤学小组将图2中的纸片展平,再次折叠,如图3,使点A与点C重合,折痕为EF,然后展平,则以点A、F、C、E为顶点的四边形是什么特殊四边形?请说明理由.(3)、创新小组用图4中的矩形纸片ABCD进行操作,其中 , ,先沿对角线BD对折,点C落在点 的位置, 交AD于点G,再按照如图5所示的方式折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M.则EM的长为cm.26. 如图,在矩形OABC中,点A在x轴上,点C在y轴上,点B的坐标是 ,将 沿直线BD折叠,使得点C落在对角线OB上的点E处,折痕与OC交于点D.
(1)、奋进小组用图1中的矩形纸片ABCD,按照如图2所示的方式,将矩形纸片沿对角线AC折叠,使点B落在点 处,则 与 重合部分的三角形的类型是.(2)、勤学小组将图2中的纸片展平,再次折叠,如图3,使点A与点C重合,折痕为EF,然后展平,则以点A、F、C、E为顶点的四边形是什么特殊四边形?请说明理由.(3)、创新小组用图4中的矩形纸片ABCD进行操作,其中 , ,先沿对角线BD对折,点C落在点 的位置, 交AD于点G,再按照如图5所示的方式折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M.则EM的长为cm.26. 如图,在矩形OABC中,点A在x轴上,点C在y轴上,点B的坐标是 ,将 沿直线BD折叠,使得点C落在对角线OB上的点E处,折痕与OC交于点D.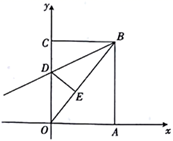 (1)、求直线OB的解析式及线段OE的长.(2)、求直线BD的解析式及点E的坐标.
(1)、求直线OB的解析式及线段OE的长.(2)、求直线BD的解析式及点E的坐标.